METODA MAXWELLA-MOHRA

Metoda M-M ma zastosowanie przy wyznaczaniu przemieszczeń w konstrukcjach statycznie wyznaczalnych oraz do wyznaczania reakcji w układach statycznie niewyznaczalnych.

Cechą charakterystyczną metody M-M jest obciążanie rozpatrywanej konstrukcji jednostkową siłą uogólnioną (siła punktowa lub moment punktowy) działającą na kierunku poszukiwanego przemieszczenia.

W przypadku wyznaczania ugięć (przesunięć) przykładamy siłę „1” do punktu konstrukcji, którego ugięcie obliczamy. Jeżeli wyznaczamy kąt ugięcia (kąt obrotu przekroju) przykładamy moment „1” w punkcie przekroju, którego kąt ugięcia obliczamy.

Dla potrzeb obliczeń inżynierskich (dla konstrukcji płaskich) wzór Maxwella-Mohra można przedstawić w postaci:

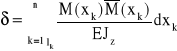
gdzie:

- poszukiwane przemieszczenie,

k - liczba przedziałów użyta do wyznaczenia równań momentów gnących,

- długość przedziału (całkujemy od 0 do wartości współrzędnej x_k na końcu przedziału),

- równania momentu gnącego w poszczególnych przedziałach dla ramy z obciążeniem
rzeczywistym,

- równania momentu gnącego w poszczególnych przedziałach dla ramy obciążonej tylko i
wyłącznie siłą jednostkową lub momentem jednostkowym,

- moduł Younga,

- moment bezwładności na zginanie przekroju poprzecznego ramy.

Całki typy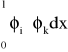
można obliczyć metodą tzw. mnożenia wykresów, jeżeli jedna z funkcji φ_i i φ_k jest liniowa na odcinku długości l. Mianowicie mnożymy pole Ω_i wykresu funkcji φ_i przez rzędną ω_k wykresu funkcji φ_k (ograniczonego prostą o stałym nachyleniu) znajdującą się pod środkiem ciężkości pola Ω_i .

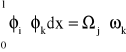
Należy zaznaczyć, że w przypadku gdy oba wykresy φ_i i φ_k są liniowe, wtedy możemy wyznaczyć pole któregokolwiek wykresu i pomnożyć je przez rzędną wykresu drugiego czyli:

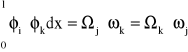
Iloczyn Ω⋅ω jest dodatni, jeżeli pola wykresów są tego samego znaku i ujemny gdy wykresy mają różne znaki.

Pola figur i położenia środków ciężkości

POLE ŚRODEK CIĘŻKOŚCI

Ω X_C

l ⋅ f
l

l ⋅ f
l

l ⋅ f
l

POSTĘPOWANIE PRZY STOSOWANIU

WZORU MAXWELLA-MOHRA:

1. Obciążyć układ siłami czynnymi i wyznaczyć reakcje podpór.

2. Obciążyć układ tylko i wyłącznie siłą jednostkową w miejscu i na kierunku poszukiwanego przemieszczenia oraz wyznaczyć reakcje podpór.

(uwaga: jeżeli poszukujemy przesunięcia pionowego - obciążamy układ siła jednostkową pionową, jeżeli poszukujemy przesunięcia poziomego - obciążamy układ siła jednostkową poziomą, jeżeli poszukujemy kąta obrotu - obciążamy układ momentem jednostkowym)

3. Przyjąć przedziały do opisu sił wewnętrznych identyczne w obu przypadkach obciążeń.

4. Napisać wyrażenia sił wewnętrznych dla obu układów.

5. Zastosować wzór Maxwella-Mohra do obliczenia poszukiwanego przemieszczenia.

POSTĘPOWANIE PRZY STOSOWANIU

SPOSOBU WERESZCZAGINA

DO OBLICZANIA CAŁEK MAXWELLA-MOHRA:

1. Sporządzić wykresy sił wewnętrznych S(x) od obciążenia układu siłami czynnymi (rzeczywiście działającymi na konstrukcje)

2. Sporządzić wykresy sił wewnętrznych S₁(x) od obciążenia układu siłą jednostkową przyłożoną w miejscu i na kierunku poszukiwanego przemieszczenia.

3. Obliczyć powierzchnię Ω i wyznaczyć środki ciężkości x_c pól wykresu S(x) odpowiadających odcinkom prostym S₁(x)

4. Wyznaczyć rzędne (wartości funkcji) ϖ=S₁(x_c) odpowiadające położeniom środków ciężkości pół wykresu S(x)

Podziału na pola wykresu S(x) dokonujemy po wykonaniu wykresu S₁(x) , kiedy wiemy ile i jakie odcinki występują na wykresie S₁(x)

W przypadku złożonego obciążenia układu korzystniej jest stosować zasadę superpozycji - wykresy S(x) mają prostą postać

Ω_i

ω_k

x

φ_k

φ_i

x

f

l

l

l

f

f

x_c

x_c

x_c

a

ax

ax²

---