Dr Oleksandr Klosov
PWSZ Legnica,
Algorytmy i Struktury Danych
Wykład
GEOMETRIA OBLICZENIOWA
[1] www.binboy.org
[2] www.algorytm.pl
[3] T.Cormen, ..., Wprowadzenie do algorytmów
PLAN
Do czego służy geometria obliczeniowa
Wzajemne położenie punktów na płaszczyźnie
Przecinanie się odcinków
Budowanie wypukłej otoczki dla zbioru punktów
Transformacja obrazów 3-D na 2-D
WPROWADZENIE
Geometria obliczeniowa - dział informatyki zajmujący się algorytmami, które rozwiązują problemy geometryczne i znajdują swoje zastosowanie w:
grafice komputerowej;
projektowaniu układów VLSI;
robotyce;
systemach CAD;
statystyce.
Rozwiązywane problemy można podzielić na:
geometrię obliczeniową na płaszczyźnie;
geometrię obliczeniową w przestrzeni 3-wymiarowej;
geometrię obliczeniową w przestrzeni n-wymiarowej.
WSPÓŁLINIOWOŚĆ TRZECH PUNKTÓW
A=(xa, ya)
B=(xb, yb)
C=(xc, yc)
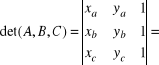
= (xayb + xbyc + xcya) - (xcyb + xbya + xayc)
ALG1
det(A,B,C) < 0
det(A,B,C) = 0
det(A,B,C) > 0
PRZYNALEŻNOŚĆ PUNKTU DO ODCINKA
A=(xa, ya)
B=(xb, yb)
C=(xc, yc)
D=(xd ,yd)
Udowodnienie, że punkt C należy do odcinka |AB|:
1 krok. Udowodnić, że punkty A,B i C leżą na jednej linii (det = 0)
2 krok. Pokazać, że współżędne x, y punktu C mieszczą się w projekcjach
odcinka AB odpowiednio na oś X oraz Y.
ALG2
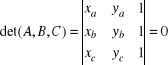
min(xa, xb) <= xc <= max(xa, xb)
min(ya, yb) <= yc <= max(ya, yb)
PRZECINANIE SIĘ ODCINKÓW
Problem:
Dano zbiór czterech punktów na płaszczyźnie (p1, p2, p3, p4). Stwierdzić czy odcinki p1p2 i p3p4 się przecinają.
Rozwiązanie:
Odcinki się przecinaja, jeżeli dowolny koniec jednego odcinka należy do drugiego odcinka;
Odcinki się przecinaja, jeżeli jednocześnie spełnia się dwa warunki:
punkty p1, p2 leżą po róznych stronach względem odcinka p3p4;
punkty p3, p4 leżą po róznych stronach względem odcinka p1p2.
PRZECINANIE SIĘ ODCINKÓW
ALG3
Dano:
p1=(x1, y1), p2=(x2, y2), p3=(x3, y3), p4=(x4 ,y4)
sign(argument) - funkcja zwracająca znak argumentu
if należy(p1, p2, p3) or
należy(p1, p2, p4) or
należy(p3, p4, p1) or
należy(p3, p4, p2)
then Przecinają się;
else
if sign(det(p1, p2, p3)) <> sign(det(p1, p2, p4)) and
sign(det(p3, p4, p1)) <> sign(det(p3, p4, p2))
then Przecinają się;
else Nie przecinają się;
PRZYNALEŻNOŚĆ PUNKTU DO OBSZARU
Dano obszar P = |P1 ... Pn|, Pi = (xi,yi).
Stwierdzić czy punkt A = (xa,ya) należy do obszaru (łącznie z granicą).
PRZYNALEŻNOŚĆ PUNKTU DO OBSZARU
Rozwiązanie
Wyznaczamy punkt B poza obszarem P taki, że B = (max(Px)+1,ay)
Punkt A należy do obszaru, jeżeli liczba boków przecinających się
z odcinkiem |AB| jest nieparzysta.
Budowanie otoczki wypukłej dla zbioru punktów
Dano zbiór punktów P = |P1 ... Pn|, Pi = (xi,yi).
Znaleźć otoczkę wypukłą - najmniejszy wielokąt wypukły taki, że każdy punkt zbioru P leży albo na brzegu wielokąta albo w jego wnętrzu.
ROZWIĄZANIE PROBLEMU
Algorytm Grahama Algorytm Jarvisa
O(n lg n) O(nh)
Każdy z algorytmów wykorzystuję przetwarzanie punktów w kolejności występowania kątów jakie tworzą z ustalonym punktem a przechodzącą przez niego osią.
OPIS ALGORYTMÓW
Algorytm Grahama
Algorytm wykorzystuję strukturę typu stos. Wszystkie punkty znajdujące się na stosie pod koniec algorytmu stanowią poszukiwaną otoczkę wypukłą. Na początku wyznacza się punkt startowy P1, jako najniżej położony na płaszczyźnie punkt. Następnie oblicza się kąty nachylenia pozostałych punktów względem P1, co ustala kolejność rozpatrywania punktów.
Punkt P2 jest brany do otoczki bezwarunkowo i odkładany na stos.
W kolejnych krokach algorytmu rozpatrywane są trzy kolejne punkty, n.p. P1, P2, P3. Jeżeli wektor P2P3 oznacza skręt w lewo względem wektora P1P2, to punkt P3 odkładamy na stos, jest on traktowany jako kandydat do otoczki. Rozpatrujemy kolejne punkty P2, P3, P4. Jeżeli wektor P3P4 skręca w prawo, to zdejmujemy punkt P3 ze stosu i przechodzimy do rozpatrywania punktów P1, P2, P4.
Algorytm kończy działanie kiedy przejdziemy przez wszystkie punkty.
Algorytm Jarvisa
Algorytm posługuje się metodą znaną jako owijanie. Po wyznaczeniu punktu początkowego, jak w poprzedniej metodzie, algorytm wykonuje powtarzające się kroki polegające na: a) wyznaczeniu kątów nachylenia punktów względem punktu bieżącego; b) wybraniu punktu o najmniejszym kącie jako punktu bieżącego oraz zaliczeniu go do otoczki.
Ponieważ po osiągnięciu w pewnym momencie najwyżej położonego punktu kąty nachylenia będą ujemne, dalsze działania opierają się na wyznaczeniu największego kąta (lub najmniejszego ujemnego). Tak powstają dwa łańcuchy: prawy, rozpoczynający się w punkcie początkowym oraz lewy, kończący się w tym punkcie, które stanowią poszukiwaną otoczkę.
KONWERSJA OBRAZÓW 3D na 2D
XP = XV + (XV - X) * ZV / (Z - ZV)
YP = YV + (YV - Y) * ZV / (Z - ZV)
gdzie:
X,Y,Z - współrzędne punktu w trzech wymiarach
XP,YP - współrzędne po konwersji na 2D
XV,YV,ZV - położenie obserwatora
CO TRZEBA UMIEĆ NA ZALICZENIE
Jak wyznaczyć wzajemne położenie trzech punktów na płaszczyźnie
Jak wyznaczyć czy dwa odcinki się przecinają
Jak działają algorytmy Grahama oraz Jarvisa
Opisać koncepcję wyznaczenia przynależności punktu do obszaru
Algorytmy i Struktury Danych, wykład, dr. O.Klosow
xa xc xb X
Y
yb
yc
ya
0

P1
P2
P3
P4
Wyszukiwarka
Podobne podstrony:
AIDS w7listy, studia, Semestr 2, Algorytmy i struktury danych AISD, AIDS
W10seek, studia, Semestr 2, Algorytmy i struktury danych AISD, AIDS
ZestawA, studia, Semestr 2, Algorytmy i struktury danych AISD, AIDS
w8grafy alg, studia, Semestr 2, Algorytmy i struktury danych AISD, AIDS
AIDS w5 rekur, studia, Semestr 2, Algorytmy i struktury danych AISD, AIDS
AIDS w3 sort1, studia, Semestr 2, Algorytmy i struktury danych AISD, AIDS
w8grafy, studia, Semestr 2, Algorytmy i struktury danych AISD, AIDS
AIDS K2 cwiczenia, studia, Semestr 2, Algorytmy i struktury danych AISD, AIDS
AIDS w7listy, studia, Semestr 2, Algorytmy i struktury danych AISD, AIDS
kolokwium1sciaga, Studia Informatyka 2011, Semestr 2, Algorytmy i struktury danych
Pojęcia algorytmy, Studia Informatyka 2011, Semestr 2, Algorytmy i struktury danych, algorytmy sciag
Algorytmy i struktury danych, AiSD C Lista04
Algorytmy i struktury danych AiSD-C-Lista01
Algorytmy i struktury danych AiSD-C-Wyklad05
Algorytmy i struktury danych AiSD-C-Lista03
egzamin info, pwr, informatyka i zarządzanie, Informatyka, algorytmy i struktury danych, aisd kolokw
Algorytmy i struktury danych, AiSD C Wyklad04 2
Algorytmy i struktury danych AiSD-C-Wyklad04
więcej podobnych podstron