Dr Aleksander Klosow

PWSZ Legnica

Algorytmy i Struktury Danych

Wykład 7

TEORIA GRAFÓW

[1] www.binboy.org

[2] www.algorytm.cad.pl

[3] P.Wróblewski, Algorytmy, struktury danych i techniki programowaniaPLAN

1. Definicja grafu

2. Podstawowe pojęcia teorii grafów

3. Metody prezentacji grafów

4. Algorytmy grafowe

DEFINICJA GRAFU

Grafem nazywamy strukturę G(V,E), gdzie V reprezentuję zbiór

wierzchołków grafu, a E - zbiór krawędzi. (ang. Vertex, Edge)

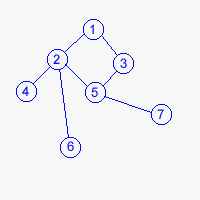
PODSTAWOWE POJĘCIA

Wierzchołek, np. 1, 2, 3; A, B, C; Student1, Student2

type W = record {dane;...} ID:integer; nastepniki: array[1..m] of ^W; end

struct W { /* dane; ... */ int ID; W** nastepniki; }

Krawędź, np. 1-2, 2-3; A-B, Student1-Student2

Łączy dwa wierzchołki, może posiadać kierunek i wagę.

5

Graf spójny

• oznacza, że dowolne dwa wierzchołki w grafie można połączyć ścieżką (która może składać się zarówno z jednej, jak i wielu krawędzi)

Graf pełny - graf, w którym każdy wierzchołek łączy się z każdym

Graf cykliczny - graf, w którym występują cykle (np.: A-B, B-C, C-A)

Graf acykliczny - graf, w którym brak cykli

Graf spójny cykliczny Graf niespójny Graf spójny acykliczny

Graf wagowy - graf, w którym wszystkie krawędzie posiadają wagi

Graf skierowany

• graf, w którym wyznaczono kierunek przejścia pomiędzy wierzchołkami

np., z 2 można przejść do 4, ale z 4 nie można przejść do 2

Następnik wierzchołka - wierzchołek, na który można przejść z danego wierzchołka przechodząc po tylko jednej krawędzi

Poprzednik wierzchołka - analogicznie...

Krawędź incydentna - krawędź łącząca dwa wierzchołki jest dla nich incydentna

Stopień wierzchołka -

w grafie nieskierowanym: liczba incydentnych (przyległych) krawędzi;

w grafie skierowanym: suma wchodzących i wychodzących krawędzi.

Graf regularny -

graf, w którym wszystkie wierzchołki są tego samego stopnia

Graf planarny -

graf, którym można przedstawić na płaszczyźnie bez przecinających się krawędzi

f-Graf -

to graf z ograniczonym stopniem wierzchołka, nie większym niż liczba f

Graf prosty - to graf bez pętli własnych i krawędzi równoległych

Pętla własna Krawędzie równoległe

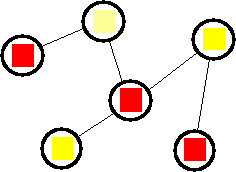
Liczba chromatyczna - to najmniejsza liczba kolorów potrzebnych do pokolorowania wierzchołków grafu tak, by żadne dwa przyległe wierzchołki

nie były tego samego koloru

Zadanie: jaka jest liczba chromatyczna grafu?

METODY PREZENTACJI GRAFÓW

Macierz sąsiedztwa

Złożoność pamięciowa: O(V²)

	1	2	3	4	5	6	7
1		1	1
2	1			1	1	1
3	1				1
4		1
5		1	1				1
6		1
7					1

Dla grafów nie wagowych - 1

Dla grafów wagowych - wagi

Lista incydencji

Dla każdego wierzchołka tworzymy listę sąsiadów

Złożoność pamięciowa: O(V+E)

1	2	3
2	1	4	5	6
3	1	5
4	2
5	2	3	7
6	2
7	5

Lista krawędzi

{1-2, 1-3, 2-4, 2-5, 2-6, 3-5, 5-7}

Złożoność pamięciowa: O(E)

Macierz incydencji

(Dla grafów skierowanych)

Złożoność pamięciowa: O(V*E)

	A	B	C	D	E
A-B	-1	1
A-C	-1		1
B-D		-1		1
C-E			-1		1
E-B		1			-1

PODSUMOWANIE

Odpowiedź: "Liczba chromatyczna..."

Zadanie: Odtworzyć postać grafów

a) G = (A-B, C-B, D-B, A-D, A-C)

b)

	1	2	3	4	5	6
1		1
2	1		1
3		1		1	1
4			1			1
5			1			1
6				1	1

c)

	A	B	C	D	E
A-B	-1	1
A-C	-1		1
A-D	-1			1
E-B		1			-1
E-C			1		-1
E-D				1	-1

ODPOWIEDZI

1. G = (A-B, C-B, D-B, A-D, A-C)

b)

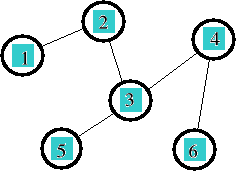
c)

A

B

A

E

C

B

D

A

C

B

D

A

E

C

B

D

A

---