Artur Fidelak środa, 07 marca 2000

I rok fizyki

Ćwiczenie nr 8

BADANIE ZJAWISKA REZONANSU MECHANICZNEGO

Lp.	n	T	A/2	w
-	-	s	^o	1/s
1	10	23,335	0,5	0,429
2	10	17,972	1,0	0,556
3	10	13,429	1,5	0,745
4	10	13,181	2,0	0,759
5	10	12,975	2,5	0,771
6	10	12,82	3,0	0,780
7	10	12,649	25,0	0,791
8	10	12,488	20,0	0,801
9	10	12,538	17,0	0,798
10	10	12,234	5,0	0,817
11	10	11,731	3,0	0,852
12	10	10,162	1,0	0,984
13	10	9,515	0,5	1,051
14	10	9,06	0,5	1,104
15	10	8,776	0,5	1,139

Ruch harmoniczny.

Ruch, który powtarza się w regularnych odstępach czasu, nazywamy ruchem okresowym (periodycznym). Przemieszczenie cząstki w takim ruchu można zawsze wyrazić przy pomocy funkcji sinus i cosinus. Ruch periodyczny często nazywamy ruchem harmonicznym.

Okresem ruchu harmonicznego jest czas trwania jednego pełnego drgnięcia, to jest czas powtarzania się każdego pełnego przemieszczenia albo cyklu.

Częstością ruchu
jest liczba drgań (albo cykli) na jednostkę czasu. Zatem częstość jest po prostu odwrotnością okresu, czyli

.

Położeniem równowagi w ruchu drgającym nazywamy położenie, w którym na punkt materialny nie działa siła wypadkowa. Przemieszczenie (linowe albo kątowe) jest to odległość (liniowa albo kątowa) drgającego punktu materialnego od położenia równowagi w dowolnej chwili.

Przemieszczenie drgającego punktu materialnego x zmienia się okresowo, zarówno co do wartości, jak i kierunku. Jego prędkość v i przyśpieszenie a także zmieniają się okresowo co do wartości i kierunku. Biorąc pod uwagę zależność F=ma, również siła F działająca na punkt materialny zmienia się okresowo.

Równanie

jest rozwiązaniem równania oscylatora harmonicznego prostego. Stałe A i δ są nieokreślone i mogą przyjmować zupełnie dowolne wartości. Stała A jest amplitudą ruchu, stąd ruchy opisane przez dane równanie mają różne amplitudy, a ten sam okres i częstość. Okres prostego ruchu harmonicznego nie zależy od amplitudy ruchu. Wielkość (ωt+δ) nazywamy fazą ruchu, przy czym δ jest stałą fazową. Dwa ruchy mogą mieć te same amplitudy i częstość, lecz różne fazy.

Dotychczas zakładaliśmy, że na rozpatrywany oscylator nie działają żadne siły tarcia. Gdyby tak było, wtedy wahadło lub ciężarek na sprężynie drgałby nieskończenie długo. W rzeczywistości w wyniku działania tarcia amplituda drgań zmniejsza się stopniowo, aż do zera. Taki ruch nazywamy ruchem harmonicznym tłumionym. Tarcie często występuje na skutek występowania oporu powietrza lub sił wewnętrznych. Wartość siły tarcia zależy od prędkości. Rozwiązaniem równania takiego ruchu jest następujące równanie

gdzie

.

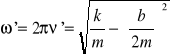
Odmienna sytuacja powstaje wtedy, gdy na ciało działa siła zewnętrzna okresowa. Jako przykład można wymienić takie zjawiska jak drganie mostu pod wpływem maszerującej przez niego kolumny żołnierzy, drgające widełki stroikowe(kamerton). Drgania jakie powstają w tych zjawiskach nazywane są drganiami wymuszonymi. Drgania wymuszone mają częstość taką, z jaką działa siła zewnętrzna, a nie taką, jaka jest częstość własna ciała. Jednak reakcja ciała zależy od stosunku, jaki zachodzi pomiędzy częstością wymuszoną a częstością własną. Kolejne impulsy, nawet niewielkie, ale następujące w odpowiednich chwilach, mogą doprowadzić do drgań o dużej amplitudzie.

Obliczenia:

Czas 100 drgań własnych wahadła T₁₀₀=125,52 s. Na tej podstawie okres T=1,256s.

Okres jednego drgania wyliczam na podstawie wzoru:

;

gdzie T_i jest okresem drgań dla kolejnych częstości, a n jest liczbą drgań w tym czasie.

T_w1=
[s].

Wyniki dla pozostałych częstości zamieszczam w tabelce na str. 1.

Częstotliwość drgań wyznaczam ze wzoru:
, żeby wykres był bardziej czytelny pomijam 2π i otrzymuję
, resztę wyników również podaję w tabelce.

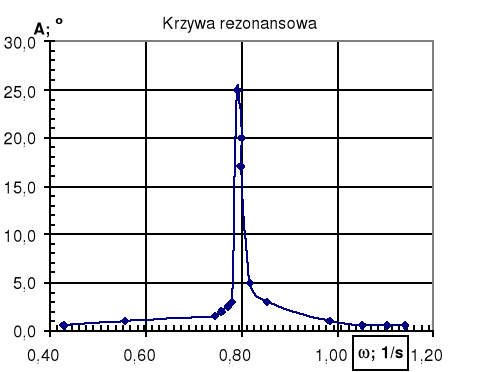
Do wyznaczenia dobroci układu Q z wykresu odczytuję szerokość krzywej rezonansu 2(Δω) w 0,7 wysokości krzywej, dl krzywej w układzie A²(ω) wartość tą odczytuje się w połowie. Wartość ta wynosi 2(Δω)=0,014 [1/s].

Stąd dobroć Q wynosi:

Wnioski:

Istnieje tylko jedna częstotliwość rezonansowa. Układ charakteryzuje się wąskim pikiem rezonansu, co oznacza że układ ma dobre właściwości wzbudzania.

Ogólnie można powiedzieć, że efekt rezonansu pozwala na uzyskanie dużych drgań przy stosunkowo niewielkiej sile wymuszającej. Gdy częstotliwość siły wymuszającej różni się od częstotliwości rezonansowej układ wykonuje chaotyczne oscylacje (ze zmienną amplitudą i częstotliwością).

Częstotliwość rezonansowa jest silnie uzależniona od współczynnika tłumienia drgań układu bez siły wymuszającej. Na podstawie badań rezonansu można wyznaczyć wartość współczynnika tłumienia.

---