Pytania egzaminacyjne z matematyki dla biotechnologów
Algebra liniowa
Ciało liczb zespolonych. Zasadnicze twierdzenie algebry.
Co to są: moduł i argument liczby zespolonej? Na płaszczyźnie zespolonej narysować zbiór liczb spełniających warunki ... .
Podać wzory Moivre'a na potęgowanie i pierwiastkowanie liczb zespolonych w postaci trygonometrycznej. Obliczyć n-tą potęgę danej liczby (lub wyznaczyć pierwiastki).
Kiedy mówimy, że wektory
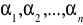
są liniowo niezależne. Sprawdzić czy dane wektory są liniowo niezależne?Jaki układ wektorów nazywamy bazą? Sprawdzić czy dane wektory są bazą przestrzeni R3.
Podać definicję rzędu macierzy. Metodą eliminacji Gaussa wyznaczyć rząd danej macierzy.
Określić warunki, przy których można mnożyć macierze. Dla danych macierzy A,B wykonać możliwe z działań A⋅B, B⋅A.
Omówić prawa działań na macierzach. Wyznaczyć macierz X z równania AX + B = C
(lub podobnego) mają dane macierze A,B,C.
Dla jakich macierzy istnieją macierze odwrotne? Wyznaczyć macierz odwrotną macierzy ... .
Podać definicję i omówić własności wyznacznika. Obliczyć wyznacznik macierzy stopnia n>3.
Sformułować twierdzenie Kroneckera-Capellego. Zastosować je do danego układu.
Układy Cramera. Definicja i sposób rozwiązywania.
Analiza matematyczna
Sformułować twierdzenie o trzech ciągach. Wykorzystać je do wyznaczenia granicy.
Podać definicję liczby Eulera e. Obliczyć granicę wykorzystując tę definicję.
Definicja pochodnej i jej interpretacja geometryczna. Sprawdzić czy dana funkcja ma pochodną w danym punkcie.
Co to jest różniczka? Wykorzystując różniczkę funkcji obliczyć przybliżoną wartość wyrażenia.
Sformułować twierdzenie Lagrange'a. Zilustrować na przykładzie danej funkcji.
Podać wzór Taylora. Napisać pięć pierwszych składników rozwinięcia w szereg potęgowy danej funkcji w otoczeniu punktu x0.
Sformułować twierdzenie (regułę) de L'Hospitala. Wykorzystać w zadaniu.
Co to jest ekstremum lokalne funkcji. Sformułować warunek konieczny i dostateczny by punkt x0 był punktem ekstremalnym.
Co to jest punkt przegięcia funkcji (wykresu funkcji). Sformułować warunek konieczny i dostateczny by punkt x0 był punktem przegięcia funkcji f.
Narysować wykres funkcji spełniającej warunki ... (dane o pochodnych i granicach w tabeli).
Sformułować twierdzenie o całkowaniu przez części. Zastosować do wyznaczenia całki ... .
Podać twierdzenie o całkowaniu przez podstawienie. Zastosować je do wyznaczenia całki ... .
Całka Riemanna i jej interpretacja geometryczna. Obliczyć pole obszaru ograniczonego wykresem funkcji (osią Ox i prostymi pionowymi).
Sformułować podstawowe twierdzenie rachunku całkowego nazywane również wzorem Newtona - Leibniza. Wyznaczyć daną całkę.
Jak definiuje się całki niewłaściwe? Obliczyć daną całkę niewłaściwą.
Równania różniczkowe o zmiennych rozdzielonych. Rozwiązać ... .
Na czym polega metoda uzmienniania stałej. Rozwiązać równanie różniczkowe... .
Pochodne cząstkowe. Różniczka zupełna funkcji dwóch zmiennych.
Wyznaczanie ekstremów lokalnych funkcji dwóch zmiennych. Wyznaczyć ... .
Całki podwójne. Zamiana na całki iterowane. Wyznaczyć ... .
Rachunek prawdopodobieństwa i statystyka matematyczna.
Co to jest przestrzeń probabilistyczna. Określić ... .
Co to jest wartość oczekiwana zmiennej losowej? Wyznaczyć wartość oczekiwaną danej zmiennej losowej.
Co to jest wariancja zmiennej losowej? Wyznaczyć wariancję danej zmiennej losowej.
Omówić rozkład dwumianowy. Zastosować w danym przykładzie.
Sformułować twierdzenie graniczne Moivre'a-Laplace'a. Korzystając z tablic dystrybuanty rozkładu normalnego N(0;1) obliczyć przybliżoną wartość prawdopodobieństwa ... .
Jakie warunki musi spełniać funkcja gęstości zmiennej losowej typu ciągłego? Wyznaczyć wartość stałej A tak, aby funkcja (zależna od A) była funkcją gęstości zmiennej losowej.
Co to jest wartość oczekiwana zmiennej losowej? Wyznaczyć wartość oczekiwaną zmiennej ... .
Co to jest dystrybuanta zmiennej losowej? Sporządzić wykres dystrybuanty zmiennej losowej o danym rozkładzie prawdopodobieństwa.
Jak zmienia się wartość oczekiwana i wariancja zmiennych losowych przy przekształceniach liniowych. Korzystając z tablicy dystrybuanty zmiennej losowej o rozkładzie N(0;1) wyznaczyć prawdopodobieństwo pewnego przedziału dla zmiennej losowej o innym rozkładzie normalnym.
Jaką statystykę przyjmuje się za estymator wartości oczekiwanej rozkładu? Z jakich statystyk korzystamy przy budowie przedziałów ufności dla wartości oczekiwanej.
Jaką statystykę przyjmuje się za estymator wariancji. Z rozkładu jakiej statystyki korzysta się
przy weryfikacji hipotez i przy budowie przedziałów ufności dla nieznanej wariancji zmiennej losowej o rozkładzie normalnym.
Wyznaczyć przedział ufności dla wartości oczekiwanej zmiennej losowej o rozkładzie normalnym o nieznanym odchyleniu standardowym, gdy dana próba prosta (n=...) dała następujące wartości estymatorów średniej i odchylenia standardowego:
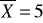
,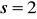
. Przyjąć poziom ufności 0,95.Jaką statystykę wykorzystuje się przy weryfikacji hipotezy o równości wartości oczekiwanych dwóch populacji o rozkładach normalnych gdy nie są znane ich odchylenia standardowe i dysponuje się wynikami małych prób? W jakich sytuacjach można zastosować test różnic?
Przy weryfikacji jakiej hipotezy statystycznej używa się statystyki o rozkładzie F Snedecora. Omówić test..
Podać definicję współczynnika korelacji i omówić jego własności.
Co to jest prosta regresji? Na czym polega metoda najmniejszych kwadratów?
Kwantyl rzędu p. Jego zastosowanie przy weryfikacji hipotez statystycznych i budowie przedziałów ufności.
Przykładowy zestaw:
Jaką funkcję nazywamy funkcją wypukłą? Wyznaczyć przedziały wypukłości dla funkcji:
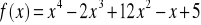
.Co to są: moduł i argument liczby zespolonej? Na płaszczyźnie zespolonej narysować zbiór liczb spełniających warunki:
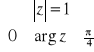
.Omówić własności współczynnika korelacji. Wyznaczyć kowariancję dla dwuwymiarowej zmiennej losowej o rozkładzie prawdopodobieństwa określonym tabelką:
X Y |
0 |
1 |
2 |
0 |
0,1 |
0,2 |
0,2 |
2 |
0,2 |
0,2 |
0,1 |
Wyszukiwarka
Podobne podstrony:
Pytania na egzamin ustny (4), Pielęgniarstwo licencjat cm umk, III rok, Neurologia i pielęgniarstwo
Pytania na egzamin ustny (1), Pielęgniarstwo licencjat cm umk, III rok, Neurologia i pielęgniarstwo
Pytania na egzamin ustny (3), Pielęgniarstwo licencjat cm umk, III rok, Neurologia i pielęgniarstwo
Pytania na egzamin ustny
Zaktualizowane pytania na egzamin ustny, egzamin na rzeczoznawcę majątkowego
PYTANIA NA EGZAMIN USTNY
pytania na egzamin ustny biochemia
pytania na egzamin !!!!!!, SWPS, Psychologia, psychologia (1 Rok), biologiczne
pytania na egzamin ustny
Pytania na egzamin ustny - zabiegi II semestr pracownia chemii kosmetycznej2, Wymagania egzaminacyj
chemia pytania na egzamin ustny semestr II
pytania na egzamin ustny, WTD, analiza matematyczna
Fw pytania, Pytania na egzamin ustny 2004 jesien, PYTANIA EGZAMINACYJNE JESIEŃ 2004
Pytania na egzamin ustny
Przykladowe Pytania na Egzamin Ustny El
pytania na egzamin ustny z ekonomii(1)
Przykladowe Pytania na Egzamin Ustny
więcej podobnych podstron