WSTĘP TEORETYCZNY:

Dokładny pomiar ciepła reakcji możliwy jest tylko dla nielicznych spośród wielu istniejących reakcji chemicznych. Precyzyjne pomiary kalorymetryczne można wykonać jedynie w przypadku reakcji przebiegających szybko, do końca i bez procesów ubocznych.

Szczególnie dogodne do pomiarów kalorymetrycznych są organiczne reakcje spalania. Źródłem większości istniejących danych termochemicznych dotyczących związków organicznych są reakcje spalania.

Celem ćwiczenia jest wyznaczenie pojemności cieplnej bomby kalorymetrycznej oraz oznaczenie ciepła spalania badanej substancji.

Ciepło spalania wyznacza się zwykle w „bombie kalorymetrycznej”. Naczyńko z odważoną próbką umieszcza się w bombie kalorymetrycznej, którą następnie wypełnia się tlenem pod ciśnieniem około 20 atmosfer. Rozżarzone prądem elektrycznym cienkiego drucika zanurzonego w próbce powoduje zapoczątkowanie reakcji. Zainicjowana reakcja przebiega w sposób gwałtowny z wydzieleniem dużej ilości ciepła. Ciepło to wyznacza się na podstawie przyrostu temperatury wody, otaczającej kalorymetr.

Podstawowe pojęcia termochemii są prostymi konsekwencjami I zasady termodynamiki: zmiana energii wewnętrznej układu (U) może dokonać się w wyniku wymiany z otoczeniem na sposób ciepła (q) lub w inny (W):

ΔU = q - W

Ciepła:

• Rozpuszczania (Q_n) jest to ilość ciepła wydzielana lub pochłonięta podczas rozpuszczania 1 mola substancji w n molach rozpuszczalnika

• Pełne ciepło rozpuszczania (Q_nas) występuje wówczas, gdy do rozpuszczenia 1 mola substancji użyjemy takiej ilości rozpuszczalnika, że powstaje roztwór nasycony

• Pierwsze ciepło rozpuszczania (Q_aq) towarzyszy rozpuszczaniu 1 mola substancji w nieskończonej ilości rozpuszczalnika (powstaje roztwór nieskończenie rozcieńczony)

• Cząstkowe ciepło rozpuszczania towarzyszy rozpuszczaniu 1 mola substancji w tak dużej ilości roztworu o określonym stężeniu, że stężenie to nie ulega zmianie

• Spalania jest to ilość ciepła wydzielana lub pochłaniana podczas spalania 1 mola substancji w n molach innej substancji

• Molowe jest to ilość ciepła potrzebna do ogrzania 1 mola substancji o 1 stopień

C_p = (δH/δT)_p

• Cv - ciepło molowe o stałej objętości C_v = (δU/δT)_v

OPRACOWANIE WYNIKÓW:

Oznaczenie pojemności cieplnej układu:

Na wstępie wyznaczone doświadczalnie przeze mnie wartości R_T przeliczam na T ze wzoru:

T =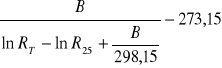

gdzie: B[deg] = 3835

R₂₅[kΩ] = 14,05 (są to wartości dla sondy czarnej)

i wyniki umieszczam w tabelach pomiarowych.

Pojemność cieplna układu kalorymetrycznego obliczam ze wzoru:

Q =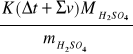

,

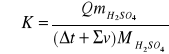
gdzie:

K - pojemność cieplna układu kalorymetrycznego,

Δt - zmiana temperatury układu kalorymetrycznego,

Σv - poprawka uwzględniająca wymianę ciepła z otoczenia podczas pomiaru,

- masa molowa kwasu siarkowego,

- masa

Q - ilość ciepła wydzielonego (względnie pochłoniętego) w kalorymetrze przez

1 mol reagenta

wartość
odczytuję z wykresu T = f(t)

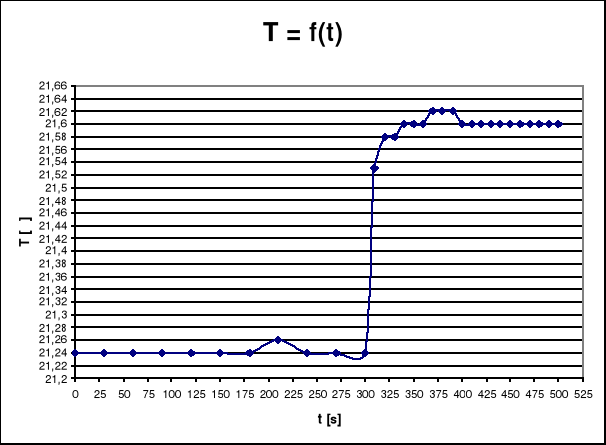
= 21,56 - 21,24 = 0,32

Znając ilość moli kwasu siarkowego i ilość wody w kalorymetrze mogę obliczyć rozcieńczenie powstałego roztworu i wyrazić go w ilościach moli H₂O rozpuszczającej 1 mol H₂SO₄.

44,44 mola wody ---- 0,02 mola kwasu

X mola wody ---- 1 mol kwasu

X = 2222 mola wody

Efekt cieplny procesu rozpuszczania wyznaczam graficznie:

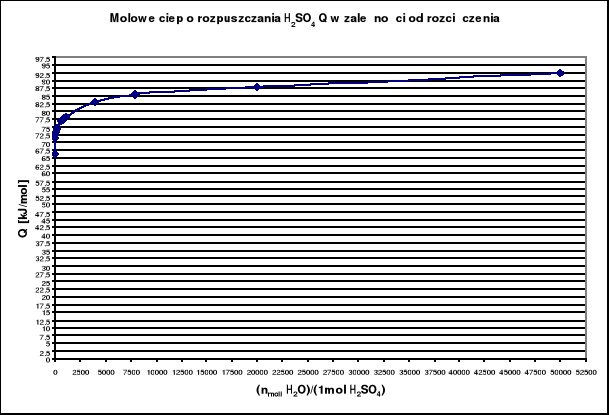
Z powyższego wykresu można odczytać, że dla X = 2222 Y wynosi 83,12

Zatem Q = 83,12 kJ/mol = 83120 J/mol

Mając dane Q mogę obliczyć pojemność cieplną układu:

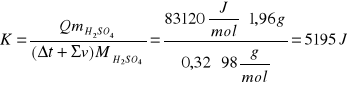
Pomiar ciepła zobojętniania kwasu H₂SO₄ zasadą NaOH:

H₂SO₄ + 2NaOH → 2H₂O + Na₂SO₄

1 mol H₂SO₄ ----2 mole NaOH

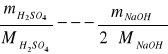
m_NaOH = 1,90 + 30% = 2,47 g

ρ =

20% --- 2,02ml NaOH

100% ---X NaOH

X = 10,1 ml NaOH

Czyli V_NaOH = 10,1 ml, V_H2O = 789,9 ml

Obliczam ciepło zobojętniania ze wzoru:

Q =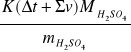

gdzie: K - pojemność cieplna układu kalorymetrycznego, K = 5195 J

Δt - zmiana temperatury układu kalorymetrycznego,

Σv - poprawka uwzględniająca wymianę ciepła z otoczenia podczas

pomiaru

- masa molowa kwasu siarkowego,
= 98 g/mol

- masa
,
= 2,32 g

Q - ciepło zobojętniania kwasu zasadą

wartość
odczytuję z wykresu T = f(t)

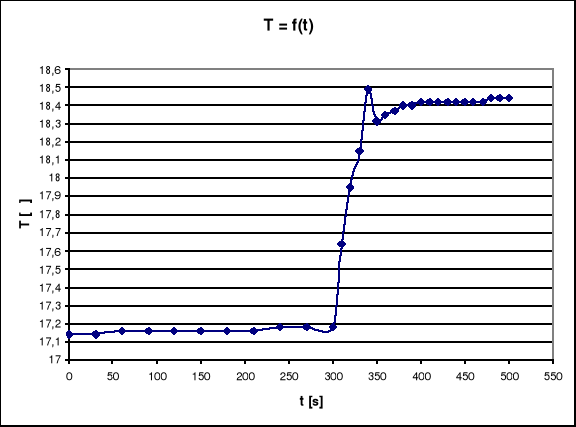
= 18,45 - 17,15 = 1,3

Q =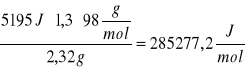

OPIS WYKONYWANEGO ĆWICZENIA:

• Oznaczenie pojemności cieplnej układu:

W naczyniu Dewara umieściłam 800 ml wody,, w uchwycie umieściłam ampułkę z dokładnie odważoną ilością H₂SO₄, włączyłam mieszadło i odczekałam ok. 5 minut dla wyrównania temperatury wszystkich części układu. Po upływie 5 minut zaczęłam odczytywać w odstępach co 30 sekund wskazania termometru Beckmana. Po zanotowaniu 11 pomiarów, stukłam bagietką ampułkę z kwasem i wykonałam 20 pomiarów co 10 sekund.

• Pomiar ciepła zobojętniania:

W ampułce odważyłam kwas siarkowy, do naczynia Dewara wlałam znaną ilość wodnego roztworu NaOH zawierającego 30% nadmiaru zasady w stosunku do kwasu. Roztwór NaOH przyrządziłam ze stężonego roztworu NaOH (ok. 20%). Dalej postępowałam tak jak w przypadku opisanym powyżej.

WNIOSKI:

Celem mojego ćwiczenia było oznaczenie pojemności cieplnej układu kalorymetrycznego, którą można było wyznaczyć wykonując pomiar kalorymetryczny dla procesu, którego efekt cieplny jest znany. W tym celu konieczne było graficzne wyznaczenie molowego ciepła rozpuszczania. Zatem pojemność cieplną wyznaczyłam ze wzoru:

Q =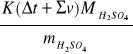

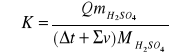
Q - była to wartość molowego ciepła odczytana przeze mnie z wykresu (odczytałam, że Q = 83,12 kJ/mol), m - była to masa kwasu siarkowego (m = 1,96g), a
- to wartość przyrostu temperatury i poprawki uwzględniającej wymianę ciepła z otoczeniem podczas pomiaru, którą to wyznaczyłam graficznie i która wyniosła 0,32. Obliczyłam, że K = 5195 J.

Druga część mojego doświadczenia dotyczyła oznaczenia ciepła zobojętniania kwasu siarkowego zasadą sodową i ów część przeprowadziłam w tym samym naczyniu (Dewara). Dzięki znanej już pojemności cieplnej (K = 5195 J) mogłam następnie obliczyć ciepło zobojętniania kwasu zasadą ze wzoru:

Q =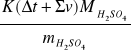

m - była to masa kwasu (m = 2,32 g), a
- to wartość przyrostu temperatury i poprawki uwzględniającej wymianę ciepła z otoczeniem podczas pomiaru, którą to wyznaczyłam graficznie i która wyniosła 1,3. Obliczona przeze mnie wartość ciepła zobojętniania wyniosła

.

G - woli formalności muszę nadmienić, iż sprawozdanie to może zawierać pewne błędy, a wynikać one mogą z nieprecyzyjnych odczytów wartości R_T. To oczywiście mogło doprowadzić do błędnych wyliczeń. Mimo wszystko z całą pewnością mogę powiedzieć, że ćwiczenie to przeprowadziłam prawidłowo - zgodnie z instrukcją.

5

---