WNiG		Rok II Grupa: 9		Zespół 4
Wytrzymałość materiałów ćwiczenia laboratoryjne.	Temat: Próba statyczna rozciągania metali			Ćwiczenie nr 1
Data wykonania 28.04.2003	Data oddania 12.05.2003		Data zalicz.	Ocena

1.Cel ćwiczenia:

Próbę statyczną rozciągania wykonujemy w celu określenia własności wytrzymałościowych i plastycznych badanego materiału:

• granicy proporcjonalności

• umownej granicy sprężystości

• wyraźnej granicy plastyczności

• wytrzymałości na rozciąganie

• modułu sprężystości podłużnej

• wydłużenia jednostkowego

• przewężenia

1. Przebieg ćwiczenia :

Podczas rozciągania badaną próbkę poddaje się działaniu jednoosiowego obciążenia mierząc jednocześnie siłę rozciągającą i wydłużenie próbki.

Wykres zarejestrowany podczas próby automatycznie odwzorowuje przebieg rozciągania w układzie siła- wydłużenie.

Na wykresie rozciągania wyróżnić można kilka charakterystycznych punktów:

1. Granica proporcjonalności. Jest to naprężenie, do którego występuje proporcjonalność naprężenia do wydłużenia jednostkowego.

Granica proporcjonalności jest granicą stosowalności prawa Hooke'a.

2. Granica sprężystości. Towarzyszy jej pojawienie się odkształceń trwałych. Trudno jest zarejestrować wartość naprężenia, przy którym pojawiają się odkształcenia trwałe. Umowną granicę sprężystości zdefiniowano jako wartość naprężenia rozciągającego, które wywołuje wydłużenie trwałe= 0,05% pierwotnej długości pomiarowej próbki.

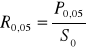
3. Wyraźna granica plastyczności. Jest to naprężenie rozciągające, po osiągnięciu którego obserwuje się wyraźny wzrost rozciąganej próbki bez wzrostu obciążenia.

4. Umowna granica plastyczności. Określa się ja dla materiałów nie mającej wyraźnej granicy plastyczności, służy jako kryterium porównawcze do oceny materiałów. Określa się ją jako wartość naprężenia rozciągającego, które wywołuje w próbce wydłużenie trwałe =0,2% pierwotnej długości pomiarowej próbki.

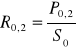
5. Wytrzymałość na rozciąganie. Jest to naprężenie rozciągające, przy którym siła obciążająca uzyskuje maksymalną wartość.
   

6. Naprężenia rozrywające. Jest to naprężenie występujące w przekroju poprzecznym próbki w miejscu przewężenia, w chwili jej rozerwania.

2. Otrzymane wyniki:

d₀= 9,7 mm

l₀= 100 mm

d_u= 5,5 mm

l_u= 125 mm

P_m= 36000 N

S₀= 73,86 mm²

S_u= 23,75 mm²

Na podstawie wzorów zamieszczonych wcześniej obliczamy następujące wielkości:

R_m= 487,4MPa

Z= 67,84 %

A₁₀= 25 %

P_u=25000 N

R_u=1052,6 MPa

Z wykresu P=P(l) określamy:

P_H=8000 N

R_H= 108 MPa

P_0,05=13000 N

R_0,05= 176 MPa

P_0,2=19000 N

R_0,2= 257 MPa

Lp	Siła P [N]	Wskazania czujników		Przyrosty		Wydłużenie	Moduł Younga
				[10^-2mm]		[10^-2mm]		l [10^-2mm]	E MPa
				l1 lewy	l2 prawy	l1	l2
1	1000	0,4	0,3	0,4	0,3	0,350	386,8
2	2000	0,5	1,0	0,5	1,0	0,750	361,0
3	3000	0,6	2,0	0,6	2,0	1,30	312,4
4	4000	0,8	2,6	0,8	2,6	1,70	318,6
5	5000	0,9	3,1	0,9	3,1	2,00	338,5
6	6000	1,0	4,0	1,0	4,0	2,50	324,9
7	7000	1,0	4,8	1,0	4,8	2,90	326,8
8	8000	1,0	5,2	1,0	5,2	3,10	349,4
9	9000	1,1	6,0	1,1	6,0	3,55	343,2
10	10000	1,1	6,8	1,1	6,8	3,95	342,8
11	11000	1,5	7,0	1,5	7,0	4,25	350,4
12	12000	2,0	8,0	2,0	8,0	5,00	324,9
13	13000	2,2	8,5	2,2	8,5	5,35	329,0
14	14000	3,0	9,1	3,0	9,1	6,05	313,3
15	15000	3,6	9,9	3,6	9,9	6,75	300,9
16	16000	4,2	10,3	4,2	10,3	7,25	298,8
17	17000	5,0	11,0	5,0	11,0	8,00	287,7
18	18000	5,2	11,8	5,2	11,8	8,50	286,7
19	19000	6,0	12,2	6,0	12,2	9,10	282,7
20	20000	6,8	13,0	6,8	13,0	9,90	273,5
21	21000	7,1	13,8	7,1	13,8	10,45	272,1
22	22000	8,0	14,2	8,0	14,2	11,10	268,3
23	23000	8,5	14,8	8,5	14,8	11,65	267,3
24	24000	9,1	15,8	9,1	15,8	12,45	261,0
25	25000	9,8	16,1	9,8	16,1	12,95	261,4
26	26000	11,9	21,0	11,9	21,0	16,45	214,0

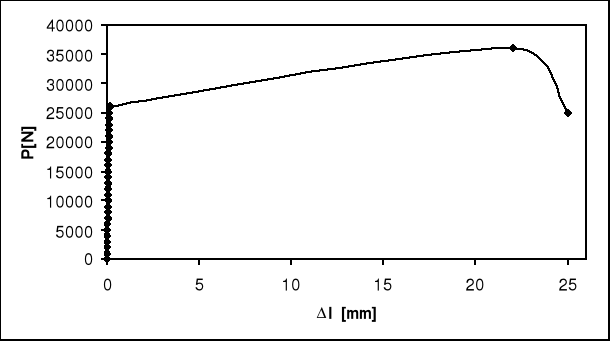
Wykres rozciągania.

Moduł sprężystości podłużnej można obliczyć tylko do granicy proporcjonalności, ponieważ jest to granica stosowalności prawa Hooke′a.

Dla próbki moduł sprężystości podłużnej równa się:

E= 273,5*10³ [MPa]

E_śr = 308*10³ [MPa]

Wynik jest porównywalny z wartościami tablicowymi. A wartość policzona ze średniej porównywalna z wartością uzyskaną z jednego punktu.

3. Wnioski:

Po przeprowadzeniu ćwiczenia możemy stwierdzić że otrzymane wyniki dają nam pewien obraz własności badanego materiału. Na podstawie otrzymanych wykresów (z maszyny wytrzymałościowej i wykonanego ręcznie możemy określić takie wielkości jak: R_H, R_0,05, R_0,2. Niestety nie możemy odczytać wyraźnej granicy plastyczności. U nas występuje ona ok. 25000 N. Przeprowadzone ćwiczenie umożliwia nam również wyznaczenie modułu sprężystości, jednak tylko do granicy proporcjonalności.

E_śr =308 *10³ [MPa]

---