I Pracownia Zakładu Fizyki PL

Nazwisko Gazda Leszek i imię							Wydział BDb.4.1.2 Grupa
Data 01,12,98 wyk. ćwicz		Numer ćwicz 5,1			Temat Pomiar SEM ogniwa ćwiczenia metodą kompensacji
Zaliczenie		Ocena	Data		Podpis

Podstawy teoretyczne:

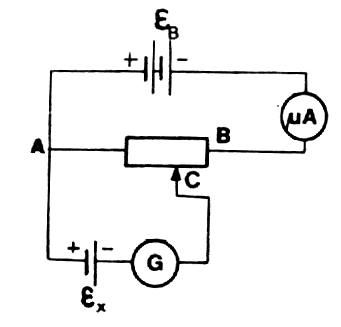
Metoda kompensacji została opracowana przez Poggendorfa. Mostek Poggendorfa stanowią dwa obwody odpowiednio ze sobą połączone (rysunek). Obwód główny składa się ze źródła prądu stałego E_B, mikroamperomierza i potencjometru, zaś obwód boczny tworzą: badane ogniwo E_X i galwanometr G. Siła elektromotoryczna E_B musi być większa od siły elektromotorycznej E_X. Pomiar polega na odpowiednim znalezieniu , takiego punktu C na potencjometrze, dal którego różnica potencjałów V_A - V_C będzie dokładnie równe E_x. W takiej sytuacji, prąd w obwodzie bocznym nie płynie a siła elektromotoryczna E_X jest skompensowana różnicą potencjału V_A - V_B.

E_X = V_A - V_B

Jeśli opór potencjometru na odcinku AC jest równy R_X, a w obwodzie głównym płynie prąd o natężeniu I to różnica potencjałów

V_A - V_C = I * R_X

,więc:

E_X = I * R_X

Wykonanie ćwiczenia

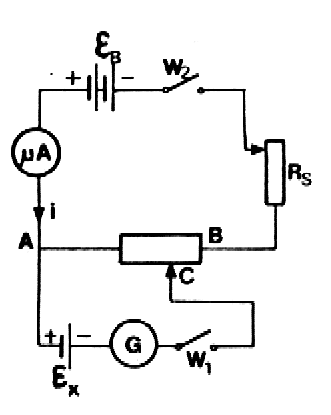
W celu wykonania ćwiczenia należy sporządzić układ zgodnie ze schematem. Obwód główny zasilany jest prądem stałym. jako potencjometr służy dekadowy dzielnik napięcia. po zamknięciu wyłącznika W₂ ustawia się natężenie prądu przy pomocy opornicy suwakowej R_S. Następnie należy zamknąć na chwilę wyłącznik telegraficzny W₁ i dobrać taka wartość oporu R_X na dzielniku napięcia, przy którym wskazania galwanometru G będą równe zeru(odpowiada to kompensacji w obwodzie bocznym). Pomiar należy wykonać pięciokrotnie przy różnych wartościach natężenia płynącego w obwodzie głównym.

Opracowanie wyników i dyskusja błędu:

Siłę elektromotoryczną E_X wyliczamy korzystając ze wzoru L:

E_X = I *Rx

_{Dane znajdują się w zeszycie pomiarów.}

_{Dane dla E1}

Lp	I [A]*10^-5	Rx[Ω]	Ex[V]	Śr Ex[v]
1.	38.9	3700	1.43930
2.	40.6	3530	1.43318
3.	50.0	2900	1.45000	1,440008
4.	54.6	2650	1.44690
5.	92.9	1540	1.43066

Dane dla E3

LP	I [A]*10^-5	Rx [Ω]	Ex [V]	Śr Ex [V]
1.	61.0	7310	4.45910
2.	106.8	4180	4.46424
3.	129.7	3440	4.46168	4.465544
4.	140.5	3180	4.46790
5.	198	2260	4.47480

Aby ocenić dokładność uzyskanych wyników, obliczam błąd względny maksymalny ∆E_X/E_X metodą różniczkową.

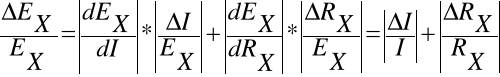
∆I = 0,5% * wskazanie

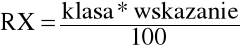
Obliczenia dla E1

Obliczam błąd względny pomiaru najbardziej odbiegającego od średniej, czyli dla pomiaru trzeciego.

ΔI=0.5%*50=0.25

δ m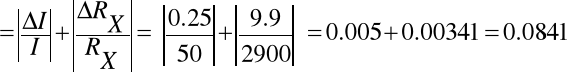

δ m%=0.0841*100%=0.841%

Obliczenia dla E3

Obliczam błąd względny dla pomiaru najbardziej odbiegającego od średniej czyli dla pomiaru piątego.

ΔI=0.5%*198=0.99

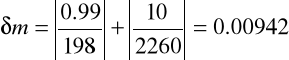
δ m.=0.00942*100%=0.942%

Wnioski:

Metoda pomiaru SEM ogniwa metodą kompensacji jest szybka i łatwa do wykonania oraz zapewnia mały błąd pomiaru.

4

---