STATYSTYKA MATEMATYCZNA
Zmienne losowe
ZMIENNA LOSOWA DYSKRETNA
Rozkładem zmiennej losowej dyskretnej nazywamy zestawienie jej możliwych wartości z odpowiadającymi im prawdopodobieństwami. Można go podać w postaci tablicy:
Rozkład zmiennej losowej dyskretnej X może być także podany w postaci analitycznej
(w postaci wzoru):Rozkład ten również można przedstawić graficznie.
Dystrybuanta zmiennej losowej dyskretnej X jest określona następująco:
X |
x1 |
x2 |
... |
xn |
P |
p1 |
p2 |
... |
pn |
![]()
![]()
![]()
Treść zadań 1-4
Dyskretna zmienna losowa ma rozkład jak podano w tabeli. Narysować rozkład prawdopodobieństwa i dystrybuantę.
Zad. 1
X |
1 |
3 |
6 |
8 |
10 |
P |
0.2 |
0.1 |
0.4 |
0.2 |
0.1 |
Zad. 2
X |
0 |
1 |
2 |
3 |
4 |
P |
0.6561 |
0.2916 |
0.0486 |
0.0036 |
0.0001 |
Zad. 3
X |
1 |
2 |
3 |
... |
P |
0.2⋅0.8k-1 |
|
||
Zad. 4
X |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
P |
1/36 |
1/18 |
1/12 |
1/9 |
5/36 |
1/6 |
5/36 |
1/9 |
1/12 |
1/18 |
1/36 |
ZMIENNA LOSOWA CIĄGŁA
Zmienna losowa, która przyjmuje wartości w przedziale [a,b] w sposób ciągły jest zmienną losową ciągłą.
Dystrybuanta F(x) zmiennej losowej X ciągłej jest funkcją ciągłą.
Gęstością prawdopodobieństwa zmiennej losowej ciągłej jest granica:
![]()
albo pierwsza pochodnia dystrybuanty:
![]()
Znając gęstość prawdopodobieństwa można znaleźć dystrybuantę ze wzoru:
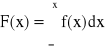
Prawdopodobieństwo tego, że zmienna losowa ciągła X przyjmuje wartość należącą do przedziału (a,b) wyznacza się z zależności:
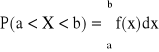
Zad. 5
Przedstawić graficznie dystrybuantę zmiennej losowej ciągłej, której rozkład nazywa się jednostajnym:
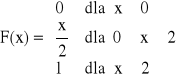
![]()
Zad. 6
Przedstawić dystrybuantę zmiennej losowej ciągłej o rozkładzie normalnym:
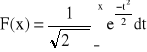
Zad. 7
Gęstośc stażu pracy osób zatrudnionych na stanowiskach kierowników wydziału podana jest zależnościami:
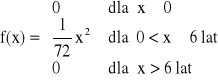
Wyznaczyć dystrybuantę i przedstawić graficznie.
Zad. 8
Czas pracy (w setkach godzin) do chwili przepalenia się żarówki jest zmienną losową X
o gęstości prawdopodobieństwa:
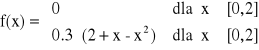
Sporządź wykres funkcji gęstości prawdopodobieństwa oraz przedstaw jej dystrybuantę.
Wyszukiwarka
Podobne podstrony:
MiBM III, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Semestr 3, StudiaIII
Zagadnienia Matematyka2, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Semest
MiBM III, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Semestr 3, StudiaIII
Statystyka5, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Semestr 4, StudiaI
statystyka1, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Semestr 4, StudiaI
Pstrona MO., POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Semestr 2, StudiaI
Metalurgia2, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Semestr 1, Studia
metalurgia ci ga www.przeklej.pl, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM
Ściąga na kolosa z wykładu, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Sem
MiBM, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Semestr 1, Studia semestr
Produkcja cegły czerwonej, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Seme
Pytania i odpowiedzi FCS ost, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, S
Matalurgia skrupt, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Semestr 1, S
więcej podobnych podstron