STATYSTYKA MATEMATYCZNA

Estymacja przedziałowa parametrów

• Przedział ufności dla średniej

Model I

Badana cecha w populacji generalnej ma rozkład normalny N (μ, *). Wartość średniej μ jest nieznana, odchylenie standardowe * w populacji jest znane. Z populacji tej pobrano próbę o liczebności n elementów, wylosowanych niezależnie. Przedział ufności dla średniej μ populacji otrzymuje się ze wzoru:

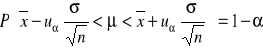
gdzie:

1-α - jest prawdopodobieństwem, przyjętym z góry i nazywanym współczynnikiem ufności (w zastosowaniach praktycznych przyjmuje się wartość 1-α ≥ 0,9)

u_α - jest wartością zmiennej losowej U o rozkładzie normalnym standaryzowanym

- średnia arytmetyczna z próby obliczona wg zależności:

Wartość u_α dla danego współczynnika ufności 1-α wyznacza się z rozkładu normalnego standaryzowanego N(0, 1), w taki sposób, by spełniona była relacja:

P{-u_α < U < u_α} = 1-α

U_α jest taką wartością zmiennej losowej o rozkładzie normalnym standaryzowanym, że pole powierzchni pod krzywą gęstości w przedziale (-u_α , u_α) wynosi 1-α, a pole pod krzywą gęstości na prawo od u_α i na lewo od -u_α wynosi po α/2. U_α jest można również wyznaczyć na podstawie dystrybuanty z zależności:

(gdzie Φ(•) jest dystrybuantą rozkładu normalnego standaryzowanego), korzystając z tablic rozkładu normalnego. U_α jest nazywane kwantylem rozkładu normalnego.

Model II

Badana cecha w populacji generalnej ma rozkład normalny N(μ, σ). Nieznana jest zarówno wartość średnia μ, jak i odchylenie standardowe σ w populacji.

Z populacji tej wylosowano niezależnie małą próbę o liczebności n (n<30) elementów. Przedział ufności dla średniej μ populacji otrzymuje się wówczas z wzoru:

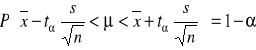
gdzie:

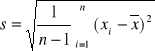
jest odchyleniem standardowym z próby.

Wartość t_α oznacza wartość zmiennej t Studenta odczytaną z tablicy tego rozkładu dla n-1 stopni swobody w taki sposób, by dla danego z góry prawdopodobieństwa 1-α spełniona była relacja:

P{-t_α<t<t_α}=1-α

Sposoby wyznaczania wartości t_α są podobne jak w modelu I.

Model III

Badana cecha w populacji generalnej ma rozkład normalny N(μ, σ) bądź dowolny inny rozkład o średniej μ i skończonej wariancji σ² (nieznanej). Z populacji tej pobrano do próby n niezależnych obserwacji, przy czym liczebność próby jest duża (co najmniej kilkadziesiąt). Wtedy przedział ufności dla średniej μ populacji wyznacza się ze wzoru jak w modelu I, z tą tylko różnicą, że zamiast σ we wzorze tym używamy wartości odchylenia standardowego s z próby.

Zadanie 1

Wytrzymałość materiału budowlanego jest zmienną losową o rozkładzie normalnym N(μ, σ). W celu oszacowania nieznanej średniej μ wytrzymałości tego materiału dokonano pomiaru wytrzymałości na n=5 wylosowanych niezależnie elementach z tego materiału. Otrzymano następujące wyniki: 20.4, 19.6, 22.1, 20.8, 21.1.

Przyjmując współczynnik ufności 1-α=0,99 zbudować przedział ufności dla średniej wytrzymałości μ tego materiału.

Zadanie 2

Chcemy oszacować średni staż pracy pracowników zatrudnionych przy obsłudze komputerów w Gliwicach. W tym celu, stosując losowanie nieograniczone, niezależne, wylosowano z populacji tych pracowników próbę liczącą n=100 osób i otrzymano następujące wyniki badania stażu pracy:

1. 4

1. 10

1. 55

1. 25

8-10 6

Przyjmując współczynnik ufności 1-α=0.90 zbudować przedział ufności dla średniego stażu pracy badanej populacji pracowników.

Zadanie 3

Oszacować żywotność (w godzinach świecenia) wyprodukowanej partii świetlówek. Wiadomo, że czas świecenia świetlówek ma rozkład normalny z odchyleniem standardowym σ=120 godzin. Wylosowana niezależnie z tej partii próba n=25 świetlówek, dała następujące wyniki pomiarów czasu ich świecenia w godzinach:

2630, 2820, 2900, 2810, 2770,

2840, 2700, 2950, 2680, 2720,

2800, 2970, 2680, 2660, 2820,

2580, 2840, 3020, 2780, 2920,

3060, 2840, 2550, 2790, 2850.

Przyjmując współczynnik ufności 0.98 oszacować metodą przedziałową średni czas świecenia świetlówek tej partii.

• Przedział ufności dla wariancji

Model I

Badana cecha w populacji generalnej ma rozkład normalny N(μ, σ) o nieznanych parametrach μ i σ. Z populacji tej wylosowano niezależnie do próby n elementów (n jest małe tj. n < 30). Z próby obliczono wariancję s². Wówczas przedział ufności dla wariancji σ² populacji generalnej określony jest wzorem:

,

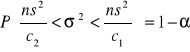
gdzie:

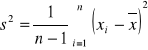
a c₁ i c₂ są wartościami zmiennej χ² wyznaczonymi z tablicy rozkładu χ² dla n-1 stopni swobody oraz współczynnika ufności 1-α w taki sposób, by spełnione były relacje:

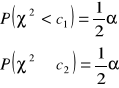
Ponieważ powszechnie używane tablice rozkładu χ² podają prawdopodobieństwo P(χ²≥χ²_α), zatem dla określonego współczynnika ufności 1-α wartości c₁ znajdujemy z tablic rozkładu χ² dla prawdopodobieństwa 1-α/2, natomiast wartość c₂ dla prawdopodobieństwa α/2.

Model II

Badana cecha w populacji generalnej ma rozkład normalny N(μ, σ) lub zbliżony do normalnego o nieznanych parametrach μ i σ. Z populacji tej wylosowano niezależnie dużą liczbę n elementów (n co najmniej kilkadziesiąt). Z próby tej obliczono odchylenie standardowe
. Wtedy przybliżony przedział ufności dla odchylenia standardowego σ populacji generalnej jest określony wzorem:

,

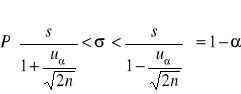
gdzie u_α jest wartością zmiennej normalnej standaryzowanej U, wyznaczoną w taki sposób dla ustalonego 1-α z tablicy rozkładu N(0, 1), by spełniona była relacja:

P{-u_α<U<u_α}=1-α.

Zadanie 4

Badając wytrzymałość elementu konstrukcyjnego dokonano n=4 niezależnych pomiarów wytrzymałości i otrzymano następujące wyniki (w MPa): 120, 102, 135, 115.

Należy zbudować przedział ufności dla wariancji σ² wytrzymałości tego elementu, przyjmując współczynnik ufności 1-α=0.96.

Zadanie 5

W celu oszacowania rozrzutu jednostkowego kosztu produkcji pewnego artykułu produkowanego przez różne zakłady, wylosowano niezależnie do próby n=80 zakładów produkcyjnych i otrzymano następujące wyniki badania tego kosztu (w tys. złotych).

Koszt jednostkowy	Liczba zakładów
20-40 40-60 60-80 80-100 100-120	10 16 24 18 12

Przyjmując współczynnik ufności 0.95 oszacować metodą przedziałową odchylenie standardowe jednostkowego kosztu produkcji tego artykułu.

Zadanie 6

W celu oceny stabilizacji procesu produkcyjnego wałków określonej średnicy, dokonano pomiarów odchyleń od nominalnej średnicy dla 150 wylosowanych wałków. Otrzymano następujący rozkład odchyleń od nominalnej średnicy (mikronach):

Odchylanie od nominalnej średnicy	Liczba wałków
0-5 5-10 10-15 15-20 20-25 25-30 30-35	2 10 25 36 45 22 10

Przyjmując współczynnik ufności 0.99 zbudować przedział ufności dla odchylenia standardowego odchyleń od nominalnej średnicy wałków.

---