Ruch jednostajny po okręgu

Ruchem nazywamy następującą w czasie zmianę położenia ciała względem wybranego układu odniesienia.
Ruch jednostajny po okręgu to ruch, w którym torem jest okrąg, a prędkość liniowa ma wartość stałą.

Okresem `T' nazywamy czas trwania jednego obiegu. Jednostką okresu jest 1 sekunda.
Częstotliwością nazywamy liczbę obiegów w jednostce czasu (np. 1s) i oznaczamy ją `f'. Jednostką okresu jest 1 herc (Hz).
1 Hz to częstotliwość ruchu, w którym jeden obieg wykonywany jest przez jedną sekundę.

Okres jest odwrotnością częstotliwości:

lub

Prędkość liniowa

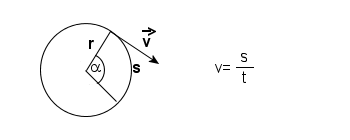
Punkt materialny poruszający się po okręgu zakreśla w pewnym czasie 't' drogę 's' równą łukowi okręgu.
Prędkością liniową nazywamy wielkość fizyczną, której miarą jest iloraz przebytej przez punkt poruszający się po okręgu drogi 's' do czasu, w którym ta droga została przebyta.
Prędkość liniowa jest wektorem stycznym do okręgu w każdym punkcie chwilowego położenia ciała.

Gdy punkt zakreśli pełen okrąg, to:

zatem...:
...a ponieważ...
...to:

.

Wartość prędkością kątową oznaczamy wielkość fizyczną, której miarą jest iloraz kąta  zakreślonego przez promień wodzący punktu poruszającego się po okręgu do czasu `t', w którym ten kąt został zakreślony.

Gdy punkt zakreśli pełen okrąg:

więc:

Związek między prędkością liniową a prędkością kątową:

Przyspieszenie dośrodkowe

Zadajmy sobie pytanie:
Dlaczego w ruchu jednostajnym po okręgu występuje przyspieszenie?

		prędkośći te mają jednakowe wartości liczbowe, ale RÓŻNE kierunki. Jeżeli prędkości i nie są sobie równe, to ich różnica, czyli przyrost prędkości jest różny od zera i wobec tego istnieje przyspieszenie:

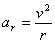
Przyspieszenie dośrodkowe, zwane tak gdyż kierunek wektora przyrostu prędkości
, a tym samym przyspieszenie, dąży do kierunku promienia, zwrot zaś jest skierowany ku środkowi okręgu.

Wzór na przyspieszenie dośrodkowe:

PODSUMOWANIE:

• wektor prędkości liniowej jest styczny do okręgu, a wektor przyspieszenia dośrodkowego jest zwrócony ku środkowi okręgu. Jest więc prostopadły do wektora prędkości liniowej.

• przyspieszenie jest konsekwencja zmiany kierunku prędkości, a nie zmiany wartości prędkości.

Siła dośrodkowa ( w układzie nieinercjalnym zwana jest siłą odśrodkową bezwładności)

Z II zasady dynamiki wiadomo, że skoro ciało posiada przyspieszenie, to musi działać jakaś siła, wywołująca to przyspieszenie.

Wzór na siłę dośrodkową:

Siła ta jest skierowana do środka okręgu.
Działanie siły dośrodkowej jest warunkiem ruchu punktu materialnego po okręgu. Powoduje zmianę kierunku wektora prędkości, a nie wartości tegoż wektora.

Punkt poruszający się po okręgu zakreśla pewien łuk, zwany też drogą liniową, zaś promień wodzący tego punktu (OA) zakreśla kąt , zwany drogą kątową. Kąt ten wyrażamy w radianach

Kąt wyrażony w radianach obliczamy ze wzoru:

s - łuk r - promień

---