Ćwiczenie 4. Metody newtonowskie i metody funkcji kary.

Wprowadzenie

Celem ćwiczenia było zapoznanie się z algorytmem minimalizacji funkcji wielu zmiennych metodami newtonowskimi oraz minimalizacji wskaźnika jakości przy istniejących ograniczeniach równościowych i nierównościowych przy użyciu metody funkcji kary.

Przebieg ćwiczenia

Funkcja wykorzystywana do obliczeń:

Metoda Newtona-Raphsona

Poniżej został przedstawiony algorytm programu wykorzystującego metody newtonowskie do wyznaczenia współrzędnych punktu minimum funkcji
.

function[Xn,licznik]=newton() %funkcja licząca minimum metodą newtonowską

E=0.001; %zadana dokładność

X0=[0;0]; %punkt startowy

licznik=0; %ilość wykonanych iteracji

delta = E;

while delta>=E, %kolejne iteracje szukające współrzędnych punktu minimum zadanej funkcji

%gradient

g=[2*X0(1,1)+2+4*((X0(1,1)+1)^3)+X0(2,1)+2;2*(X0(2,1)+2)+4*((X0(2,1)+2)^3)+X0(1,1)+1];

%hesjan

H=[2+12*((X0(1,1)+1)^2),1;1,2+12*((X0(2,1)+2)^2)];

%wyznaczenie współrzędnych punktu minimum

Xn=X0-H^(-1)*g;

delta = abs(Xn-X0);

X0=Xn;

licznik = licznik +1; %zliczanie iteracji

end

if delta<E

%wartość minimum funkcji dla współrzędnych wektora Xn

Wartosc=(Xn(1,1)+1)^2+(Xn(2,1)+2)^2+(Xn(1,1)+1)^4+(Xn(2,1)+2)^4+(Xn(1,1)+1)*(Xn(2,1)+2);

End

W newtonowskich metodach poszukiwania minimum do wyznaczenia kolejnych przybliżeń punktu minimalnego wskaźnika jakości, wykorzystywana jest informacja o wartości funkcji, wartości jej gradientu i hesjanu w otoczeniu ostatniego przybliżenia punktu minimalnego. Poszukiwania odbywają się do momentu uzyskania zadanej dokładności.

Poniżej przedstawiono wyniki kilku testów przy zmianie punktu startowego oraz dokładności E=0.001.

X0	Xn	F(Xn)	Licznik
(0;0)	(-1;-2)		7
(10;10)	(-1;-2)		11
(-5;-5)	(-1;-2)		9
(1;2)	(-1;-2)	0	9
(-1;-2)	(-1;-2)	0	1

Metoda Carolla, Fiacco, McCormicka funkcji kary

Przy użyciu metody funkcji kary szukaliśmy minimalizacji wskaźnika jakości przy istniejącym ograniczeniu nierównościowym. Do obliczeń została wykorzystana powyższa funkcja
przy istniejącym ograniczeniu nierównościowym w postaci
. Kod programu wykorzystującego tę metodę został przedstawiony poniżej.

function[licznik,x0]=funkcja_kary()

licznik=0; %zliczanie iteracji

delta_r=1.1; %zmiana współczynnika kary jako ciągu geometrycznego

%PRZY WYBORZE DELTY NALEŻY PAMIĘTAĆ ŻE MUSI ONA BYĆ WIĘKSZA OD 1 BY CIĄG GEOMETRYCZNY MALAŁ

r=50;

r_k=r/delta_r; %współczynnik kary

%OGRANICZENIE NIERÓWNOŚCIOWE : x1+x2<=3

%funkcja licząca współrzędne x1 i x2

x0=fminunc(@(x) (x(1)+1)^2+(x(2)+2)^2+(x(1)+1)^4+(x(2)+2)^4+(x(1)+1)*(x(2)+2)-r_k*(1/(x(1)+x(2)-3)),[0;0]);

E=0.001; %szukana dokładność współczynnika kary

while r>=E,

licznik=licznik+1;

r_k=r/delta_r;

r=r_k;

x0=fminunc(@(x) (x(1)+1)^2+(x(2)+2)^2+(x(1)+1)^4+(x(2)+2)^4+(x(1)+1)*(x(2)+2)-r_k*(1/(x(1)+x(2)-3)),[0;0]);

%funkcja zmodyfikowana

end

Istotą metody funkcji kary jest zastąpienie procesu minimalizacji funkcji celu problemem minimalizacji zmodyfikowanej funkcji , która jest sumą pierwotnej funkcji celu i funkcji kary za nałożone ograniczenia. Stosowana metoda modyfikuje funkcje kary stosowane w kolejnych iteracjach, tak aby były coraz słabsze. Metodę tę stosujemy zmieniając wartość współczynnika kary po to, aby zbliżać się z punktem optymalnym wskaźnika jakości do granicy spełnienia ograniczeń nierównościowych. Do zmiany współczynnika kary posłużono się ciągiem geometrycznym pozwalającym na szybszą minimalizację tego współczynnika.

Poniżej przedstawiono wyniki kilku testów przy zmianie punktu startowego oraz delty(r).

X0	Delta(r)	Xn	Licznik
(10;10)	1.1	(-1.007;- 2.0017)	114
(1;1)	1.1	(-1;-2)	114
(0;0)	15	(-1;-2)	4
(1;1)	5	(-1;-2)	7
(2;2)	10	(-1;-2)	5

Rozwiązanie podstawowej funkcji
metodą analityczną.

Obliczamy:

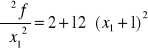
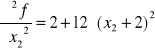
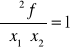
Następnie rozwiązujemy układ równań:

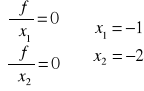
więc w punkcie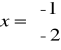
istnieje ekstremum funkcji

Badamy znak drugiej pochodnej:

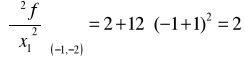
w punkcie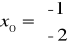
znajduje się minimum lokalne

Wnioski i spostrzeżenia

1. Podczas przeprowadzania kolejnych prób przy zmianie punktu startowego metodą newtonowską można było zauważyć zależność: im punkt startowy bliższy punktu
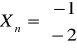
   , tym mniej iteracji potrzebnych było do wyznaczenia współrzędnych punktu minimum funkcji. Natomiast współrzędne te we wszystkich próbach wyliczane były dokładnie.

2. Podanie punktu startowego mieszczącego się w ograniczeniach zadanych w metodzie funkcji kary pozwoliło na szybsze wyznaczenie współrzędnych punktu minimum funkcji w porównaniu z wyznaczeniem go dla punktu startowego spoza ograniczenia. Ponadto dla punktu startowego spoza ograniczenia wyznaczone współrzędne punktu minimum funkcji były jedynie zbliżone do wyniku oczekiwanego.

3. Podczas wykorzystywania metody funkcji kary należy z uwagą dobierać punkt startowy, co pozwoli na dokładniejsze oraz szybsze wyznaczenie minimalnej wartości zadanej funkcji.

4. Metoda funkcji kary pozwala wyznaczyć minimum funkcji przy istniejących ograniczeniach przez co staje się bardziej uniwersalna od metody newtonowskiej.

5. Niektóre elementy algorytmu metody funkcji kary czynią ją niepozbawioną błędów. Przykładem może być składnik funkcji zmodyfikowanej ilustrujący ograniczenie nierównościowe. Pojawia się sytuacja, w której wykonywane byłoby dzielenie przez 0, przy odpowiednio dobranych parametrach, co jak wiadomo, jest niedopuszczalne. Zatem posługujący się tą metodą zobligowany jest do uwzględnienia uchybień jakie pojawiają się w trakcie stosowania tej metody.

6. Obie metody podczas testów dawały wyniki zgodne z wynikiem wyznaczonym metodą analityczną. Liczba potrzebnych iteracji zależała od wyboru punktu startowego X₀, zadanej dokładności E oraz delty(r) z jaką zmieniał się współczynnik kary.

---