AISDE - Kolokwium 2 16 czerwca 2008.

podpis

Zadanie 1 (4p)

Słownik zaimplementowano w tablicy nie­up­o­­rząd­kowanej. Algorytm insert_t wstawia do słownika klucze od lewej strony. Do słownika wstawiono za pomocą insert_t ko­lej­no klucze 1,2,...,n. Obliczyć złożoność ocz­e­kiwaną A(n) algorytmu search_t wyszuku­jącego sek­wen­cyj­nie klucze k od lewej strony. Wy­szu­­ki­wa­ne klucze mają rozkład równo­mier­ny w zbiorze [1,2,...,2n]. Operacją dominu­jącą jest porów­nanie kluczy.

Prawdopodobieństwo, że wyszukiwany klucz znajduje się w słowniku wynosi...................... Złożoność czasowa operacji insert_t wynosi Θ(g(n)). g(n)=................................................. A(n)=..............................................................

Zadanie 2 (4p)

Na początku słownik BST zawierał element o kluczu 2. Do słownika wstawiono dwa klucze ze zbioru [1,...,n] algorytmem insert_bst. Złożoność czasowa każdego wsta­wie­nia wy­nosi jedno porównanie kluczy. Podać wartości wstawionych kluczy.

Wstawione elementy to: ................................. Ile istnieje różnych rozwiązań problemu? ......................................................................... Narysować BST po wstawieniu kluczy.

Zadanie 3 (4p)

Słownik zaimplementowano w tablicy upo­rz­ąd­kowanej, która ma postać: [a,b,c,d,e]. Wy­szukanie za pomocą search_tu_ bin klucza 4 było pomyślne i miało złożo­ność opty­mi­sty­cz­ną, a wyszukanie klucza 6 było po­myś­lne i miało złożoność pesymistyczną. Wyszukanie klucza 2 oraz innych istniejących kluczy za pomocą search_tu_int było po­myślne i miało złożoność optymistyczną.

Określić elementy tablicy: a=.................................................. b=.................................................. c=.................................................. d=.................................................. e=..................................................

Zadanie 4 (4p)

Tekst ma postać T=[a,b,c,d,e], wzorzec ma postać P=[f,g,h], alfabet V={0,1}. Złożoność wyszukiwania algorytmem Naive wynosi 3 porównania elementarnych symboli, a algo­rytm Rabina-Karpa wykonał 3 razy strng_comp licząc modulo q, gdzie q=2. Określić wszystkie możliwe T i P.

Ile rozwiązań posiada zadanie? ................ T=[...........................................................] P=[.....................] T=[...........................................................] P=[.....................] T=[...........................................................] P=[.....................] T=[...........................................................] P=[.....................]

Zadanie 5 (4p)

Algorytm KMP stosujemy dla 4 wariantów danych: a) |T|=n=100 i |P|=m=100, b) |T|=n=10 i |P|=m=10 oraz c) |T|=n=100 i |P|=m=10, d) c) |T|=n=10 i |P|=m=100. Wskazać jeśli istnieje wariant pesymistyczny, optymistyczny i niewykonalny.

Wariant pesymistyczny .................................. Wariant optymistyczny .................................. Wariant niewykonalny ...................................

Zadanie 6 (4p)

Automat wyszukujący wzorzec P=[a,b,a,c] nad V={a,b,c} jest w pewnej chwili w stanie q=3. Po wczytaniu symbolu x przechodzi w stan q=2. Określić x. Obliczyć σ([P3,x]). Ile elementów zawiera tablica przejść tego automatu? Ile stanów akceptujących zawiera automat?

x=................................................................. σ([P3,x])=..................................................... liczba elementów tablicy przejść = ............. liczba stanów akceptujących=......................

Zadanie 7 (4p)

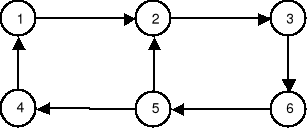
Podany graf skierowany przeszukujemy algo­ryt­mem DFS z wierzchołka 1. Opisać atrybuty d, f i p wierzchołków, pogrubić drzewo przeszukiwania. Podać liczbę cięciw powrotnych. Wypisać wierzchołki posorto­wa­ne topolo­gi­cznie. Ile składowych silnie spój­nych posiada graf?

liczba cięciw powrotnych=............................... posortowanie topologiczne: ............................. liczba składowych silnie spójnych = ...............

Zadanie 8 (4p)

Dla grafów o n wierzchołkach i m krawędziach prawdziwe są następujące zdania.

Maksymalny spójny podgraf acykliczny gr­afu nieskiero­wanego ma (ile?)............ krawędzi. Sumaryczna długość list sąsiedztwa grafu skierowanego wynosi ............................... Jeżeli w DFS pierwszemu odwiedzonemu wierzchołkowi grafu skierowanego nada­no atrybut d=1 to jego atrybut f przyjmie wartość.................................................... Jeżeli za operację dominującą przyjmiemy wywołanie trzech funkcji obsługujących kolejkę to złożoność czasowa algorytmu BFS wyniesie............................................

Zadanie 9 (4p)

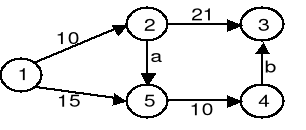
Dla podanego grafu ważonego wykonujemy z wierzchołka 1 algorytm Dijkstry. Znaleźć maksymalne, całkowite, dodatnie a i b takie żeby ście­żka p(1,3)= {1,2,5,4,3} była naj­kró­tszą ście­żką od wierz­chołka 1 do 3 i żeby na­leżała ona do drzewa przeszukiwania. Dla tych a i b opi­sać graf atrybutami d (na po­czątku i po kolejnych relaksacjach, np. inf/5/2) i pop otrzymanymi po wykona­niu algorytmu i pogrubić drzewo najkrótszych ścieżek. Określić wagę najkrótszej ścieżki δ(1,3).

maksymalne a=......................... maksymalne b=......................... δ(1,3)=..............................................................

---