Kolokwium I rok 2008/2009

Zadanie 5 : a) Wykazać, że krzywizna i skręcanie krzywej
są sobie równe.

b) Co znaczy, że punkt
jest punktem wyprostowania krzywej? Czy krzywa z punktu a) ma punkt wyprostowania?

Rozwiązanie:

1. Potrzebne wzory do obliczeń:

1. Krzywizna krzywej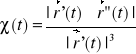
   

2. Skręcenie krzywej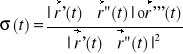
   

2. Parametryzacja prostej L

;

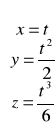
gdzie

3. Obliczenie potrzebnych nam danych do wzorów

1. Pochodne z
   :

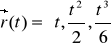
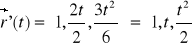
pochodna I rzędu z

pochodna II rzędu z

pochodna III rzędu z

2. Zależności z wzorów:

• 
  

• 
  

• 
  

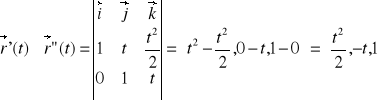
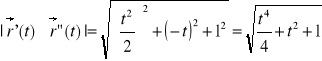
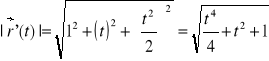
4. Obliczenie krzywizny krzywej

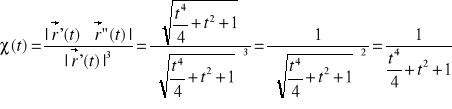
5. Obliczenie skręcenia krzywej

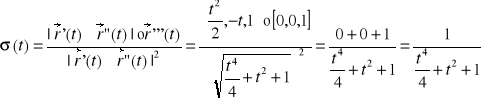
6. Wnioski:

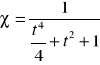
i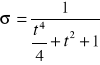
stąd:

krzywizna krzywej jest równa jej skręceniu

b)

• Punkt
  jest punktem wyprostowania krzywej
  , wtedy gdy
  

• Aby prosta
  miała punkt wyprostowania:

, więc:

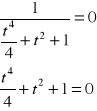
zawsze będzie
więc krzywa
nie posiada punktu wyprostowania.

Odpowiedź:

a) Krzywizna i skręcenie są sobie równe.

b) Krzywa nie posiada punktu wyprostowania.

Autor: Anna B. grupa 2

---