Wydział EAIiE |
Filip Balicki™ Adam Borejczuk™
|
Rok I |
Grupa I |
Zespół 11 |
|
Pracownia Fizyczna |
Temat: Busola Stycznych |
Nr ćwiczenia 2 |
|||
Data wykonania 03.o3.00 |
Data oddania 06.03.00 |
Zwrot do poprawy
|
Data oddania 13.03.00 |
Data zaliczenia
|
Ocena
|
Sprawozdanie z ćwiczenia nr 41
BUSOLA STYCZNYCH
Cel ćwiczenia:
Naszym zadaniem było wyznaczenie składowej poziomej ziemskiego pola magnetycznego. W tym celu musieliśmy zapoznać się z budową i działaniem busoli stycznych.
Busola stycznych składa się z solenoidu oraz igły magnetycznej umieszczonej w centrum cewki kołowej.
Zasada działania:
Pod wpływem płynącego prądu w cewce wokół zwojów, wytwarza się pole magnetyczne. Chcąc zmierzyć jego wartość w centrum busoli, korzystamy ze wzoru Biota-Savarta.
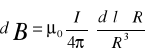
μ0 = 4Π*10-7 Vs/Am
I - natężenie prądu
R - wektor łączący element dl i punkt, w którym obliczamy pole.
Zgodnie z własnościami iloczynu wektorowego, kierunek wektora dB jest prostopadły do płaszczyzny wektorów dl oraz R. W tym przypadku wektor dl jest prostopadły do wektora R, a więc iloczyn wektorowy dl×R zastąpić można zwykłym iloczynem Rdl. Sumowanie przyczynków dl sprowadza się do sumowania elementów długości dl, co stanowi obwód cewki dany wzorem 2ΠR.
![]()
Ostatecznie dla środka cewki kołowej, złożonej z n zwojów, wartość indukcji pola magnetycznego wynosi
Pole magnetyczne działa na igłę magnetyczną, która jest tak przytwierdzona, by mogła się obracać tylko w poziomie. Wokół igły jest skala kątowa na której odczytujemy wychylenie igły.
Ćwiczenie rozpoczynamy od wypoziomowania busoli, oraz ustawienia jej tak, by igła pokrywała się z płaszczyzną południka ziemskiego. Następnie zestawiamy obwód elektryczny według schematu, oraz mierzymy obwód cewki. Dla każdej liczby zwojów (4,16,40) wykonujemy pomiary natężenia prądu przy wychyleniu igły o kolejno 30, 40, 50, i 60 stopni w obie strony.
Tangens kąta między igłą magnetyczną a południkiem wyraża się poprzez stosunek B/B0 gdzie:
B - długość wektora indukcji pola magnetycznego cewki
B0 - szukana wartość poziomej składowej wektora indukcji ziemskiego pola magnetycznego
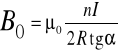
Podstawiając tą zależność do wyżej wymienionego wzoru na B otrzymamy:
Błędy:
Oczywiście, jak każdy pomiar i ten będzie obarczony pewnym błędem. Ponieważ wielkość B0 nie jest bezpośrednio mierzona, lecz otrzymujemy ją z obliczeń, skorzystamy z zasady przenoszenia błędów, która mówi, że każdy otrzymany wynik jest obarczony standardowym błędem wyliczanym ze wzoru
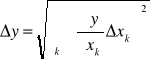
B0 jest zależne od trzech wielkości obarczonych następującymi błędami:
R ΔR = 0,001
α Δα = 1/360
I ΔI = zakres amperomierza/75 (podziałka)
Po obliczeniu pochodnych cząstkowych otrzymujemy
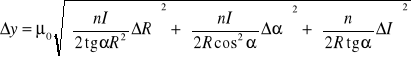
Błąd średniej w przypadku wyliczania błędu metodą przenoszenia jest równy średniej geometrycznej błędów.
Wyniki pomiarów
Przedstawia poniższa tabela:
Liczba zwojów |
Prąd [A] |
Kąt [ st] |
Prąd przeciwny [A ] |
Średni Prąd [A] |
Zakres miernika [A] |
B [μT] |
Błąd |
4 |
0,64 |
30 |
0,65 |
0,65 |
0,75 |
21,4307 |
0,3481 |
4 |
0,96 |
40 |
0,96 |
0,96 |
1,50 |
22,1184 |
0,4767 |
4 |
1,36 |
50 |
1,35 |
1,36 |
1,50 |
22,0622 |
0,3787 |
4 |
1,94 |
60 |
1,94 |
1,94 |
3,00 |
21,6540 |
0,6164 |
16 |
0,17 |
30 |
0,17 |
0,17 |
0,30 |
22,7702 |
0,5450 |
16 |
0,25 |
40 |
0,25 |
0,25 |
0,75 |
22,5792 |
0,9302 |
16 |
0,34 |
50 |
0,35 |
0,35 |
0,75 |
22,0622 |
0,6787 |
16 |
0,50 |
60 |
0,48 |
0,49 |
0,75 |
22,3237 |
0,6194 |
40 |
0,06 |
30 |
0,06 |
0,06 |
0,08 |
21,4307 |
0,3473 |
40 |
0,10 |
40 |
0,09 |
0,10 |
0,15 |
22,1184 |
0,4764 |
40 |
0,13 |
50 |
0,13 |
0,13 |
0,15 |
21,7378 |
0,3761 |
40 |
0,19 |
60 |
0,20 |
0,19 |
0,30 |
21,4307 |
0,6156 |
Z otrzymanych wyników możemy wyliczyć średnią wartość składowej poziomej ziemskiego pola magnetycznego wraz z odchyłką.
Bśr = 21,9765 ± 1,9335 [μT]
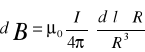
![]()
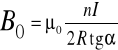
Wyszukiwarka
Podobne podstrony:
spr41 v2.0, Labolatoria fizyka-sprawozdania, !!!LABORKI - sprawozdania, 41 - Busola Styczna
41konspekt, Labolatoria fizyka-sprawozdania, !!!LABORKI - sprawozdania, Lab, !!!LABORKI - sprawozdan
KonspGC41, Labolatoria fizyka-sprawozdania, !!!LABORKI - sprawozdania, 41 - Busola Styczna
busolka, Labolatoria fizyka-sprawozdania, !!!LABORKI - sprawozdania, Lab, !!!LABORKI - sprawozdania,
WYDZIA~1, Labolatoria fizyka-sprawozdania, !!!LABORKI - sprawozdania, Lab, !!!LABORKI - sprawozdania
Fizyka 25a, Labolatoria fizyka-sprawozdania, !!!LABORKI - sprawozdania, 25 - Interferencja fal akust
spr-122, Labolatoria fizyka-sprawozdania, !!!LABORKI - sprawozdania, Lab, !!!LABORKI - sprawozdania,
Fizyka cw 123 wyniki, Labolatoria fizyka-sprawozdania, !!!LABORKI - sprawozdania, Lab, !!!LABORKI -
półprzewodnikowe złącze p-n, Labolatoria fizyka-sprawozdania, !!!LABORKI - sprawozdania, Lab, !!!LAB
LAB113, Labolatoria fizyka-sprawozdania, !!!LABORKI - sprawozdania, Lab, !!!LABORKI - sprawozdania,
laborka37, Labolatoria fizyka-sprawozdania, !!!LABORKI - sprawozdania, Lab, !!!LABORKI - sprawozdani
Wyniki do ćwiczenia 82 dla dave, Labolatoria fizyka-sprawozdania, !!!LABORKI - sprawozdania, Lab, !!
LAB 0 P, Labolatoria fizyka-sprawozdania, !!!LABORKI - sprawozdania, Lab, !!!LABORKI - sprawozdania,
lab73moja, Labolatoria fizyka-sprawozdania, !!!LABORKI - sprawozdania, Lab, !!!LABORKI - sprawozdani
LAB 33, Labolatoria fizyka-sprawozdania, !!!LABORKI - sprawozdania, Lab, !!!LABORKI - sprawozdania,
Elektroliza ćw. 2 i 5, Labolatoria fizyka-sprawozdania, !!!LABORKI - sprawozdania, Lab, !!!LABORKI -
96lab2-rob, Labolatoria fizyka-sprawozdania, !!!LABORKI - sprawozdania, 96 - Dozymetria promieniowan
więcej podobnych podstron