Kinematyczne równanie ruchu to pewna zależność (bądź układ zależności), określająca położenie ciała w przestrzeni w funkcji czasu.

Postać wektorowa kinematycznego równania ruchu to zależność określająca wektor położenia ciała jako funkcję czasu: r=r(t)

W praktyce korzysta się jednak zwykle ze skalarnej postaci kinematycznego równania ruchu. Jest ona (w trójwymiarowej przestrzeni) określona następującym układem:

Obie postaci kinematycznego równania ruchu łączy następujący związek:

są wektorami jednostkowymi skierowanymi zgodnie z osiami układu współrzędnych. Nazywa się je wersorami

Droga to długość odcinka krzywej (prostej), jaką pokonuje ciało lub punkt materialny podczas swojego ruchu.

Droga jest sumą dróg przebytych przez ciało w niewielkich odcinkach czasowych, co wyrażają wzory:

W szczególnych przypadkach. Dla ruchu jednostajnego, prędkość jest stała, dlatego:

dla t₀ = 0, wzór w postaci funkcji przebytej drogi od czasu:

Dla ruchu jednostajnie przyspieszonego prędkość wyraża wzór v = v₀ + at, dlatego:

gdzie:

s - droga v - prędkość ciała (punktu) t - czas ruchu v₀ - prędkość początkowa a - przyspieszenie t₀ - chwila początku ruchu t₁ - chwila końca ruchu. v(t) - funkcja prędkość ciała (punktu)

Droga nie oznacza odległości pomiędzy dwoma punktami wyznaczającymi początek i koniec ruchu; drogę liczy się po torze ruchu czyli po krzywej, po której porusza się ciało. Inaczej, jest to długość odcinka tej krzywej, wyznaczonego przez punkt początkowy i końcowy ruchu.

Jednostkami drogi są jednostki długości, w układzie SI jest to metr.

W pojazdach przebytą drogę mierzy licznik kilometrów.

Przemieszczenie: jest to wektor łączący położenie początkowe z końcowym. Wektor ten nie podaje informacji o drodze.

Jeżeli punkt materialny porusza się od położenia A do położenia B jego przemieszczenie przedstawia prosta linia łącząca A i B. Kierunek przemieszczenia możemy określić rysując w pobliżu punktu B ostrze strzałki, co wskazuje że przemieszczenie rzeczywiście odbywało się od punktu A do B. Rzeczywista droga przebyta przez punkt materialny nie pokrywa się z wektorem przemieszczenia AB.

Wielkości, które zachowują się jak przemieszczenia nazywane są wektorami.

Prędkość to:

wektorowa wielkość fizyczna wyrażająca zmianę wektora położenia w jednostce czasu.

skalarna wielkość oznaczająca przebytą drogę w jednostce czasu lub tylko wartość prędkości zwana przez niektórych szybkością.

Jednostka prędkości w układzie SI to metr na sekundę.

Prędkość średnia w ruchu prostoliniowym to iloraz przemieszczenia i różnicy czasów w których miało ono miejsce, ogólnie wyrażone wzorem:

Prędkość średnia - to także taka prędkość jaką uzyskałoby ciało, gdyby cały czas poruszało się ruchem jednostajnym.

Prędkość jako wielkość niewektorowa [edytuj]

W wielu przypadkach prędkość rozumiana jest jako stosunek drogi do czasu jej przebycia. Tak jest rozumiana intuicyjnie, a także w wielu problemach fizycznych.

Przy czym droga jest rozumiana jako długość odcinka krzywej, po której porusza się ciało, wyznaczonego przez punkt początkowy i końcowy ruchu.

Prędkość chwilowa: to

Oraz prędkość średnia

Przy czym prędkość chwilowa niewektorowa jest równa modułowi (wartości) prędkości chwilowej wektorowej, średnia prędkość niewektorowa jest większa lub równa modułowi średniej prędkości wektorowej.

Przyspieszenie - wektorowa wielkość fizyczna wyrażająca zmianę prędkości w czasie.

Przyspieszenie definiuje się jako pochodną prędkości po czasie (jest to miara zmienności prędkości). Przyspieszenie jest wielkością wektorową, gdzie wartość tego wektora jest równa wartości pochodnej prędkości względem czasu w danej chwili. Jeśli przyspieszenie jest skierowane przeciwnie do kierunku prędkości ruchu, to jest czasem nazywane opóźnieniem.

Definicja Jeżeli mamy dany wektor
określający położenie punktu materialnego i wektor
określający prędkość tego punktu, to przyspieszenie
tego punktu obliczamy w następujący sposób:

Jednostka przyspieszenia w układzie SI to metr na sekundę do kwadratu. Przyspieszenie średnie

Przyspieszenie chwilowe (czyli po prostu przyspieszenie)

Równanie ruchu - równanie różniczkowe, określające szybkość zmian pewnych wielkości fizycznych (np. prędkości, położenia) jako funkcję aktualnego stanu układu. Przez równanie ruchu najczęściej rozumiemy drugą zasadę dynamiki Newtona, zapisaną w postaci równania różniczkowego. W ogólności równanie ruchu dla pojedynczej cząstki można zapisać jako:

Kinematyczne równanie ruchu to pewna zależność (bądź układ zależności), określająca położenie ciała w przestrzeni w funkcji czasu.

Postać wektorowa kinematycznego równania ruchu to zależność określająca wektor położenia ciała jako funkcję czasu:

Ruch zmienny - (ruch niejednostajny), w którym prędkość zmienia się. Zmiana prędkości może dotyczyć zarówno jej wartości jak i kierunku.

Ruch zmienny jest przeciwieństwem (dopełnieniem) ruchu jednostajnego prostoliniowego.

W zależności od charakteru zmiany prędkości wyróżnia się przypadki szczególne ruchów zmiennych:

Ruch prostoliniowy zmienny - ruch, w którym nie zmienia kierunek prędkości, ale wówczas musi zmieniać się wartość prędkości. Jeśli zmiana prędkości w ruchu prostoliniowym jest stała, mówi się o ruchu jednostajnie przyspieszonym lub opóźnionym (w tym drugim wartość przyspieszenia przybiera wartości ujemne).

Ruch krzywoliniowy - ruch, w którym zmienia się kierunek ruchu a nie zmienia się wartość prędkości. Szczególnym przypadkiem tego ruchu jest ruch jednostajny po okręgu, w którym zmiana kierunku jest jednostajna.

Pozostałe przypadki ruchu zmiennego - ruch, w którym zmiana się zarówno kierunek jak i wartość prędkości, przykładem takiego ruchu może być ruch zmienny po okręgu.

Ruch jednostajny - ruch, w którym w takich samych przedziałach czasowych ciało pokonuje takie same odcinki drogi.

Warunek ten odpowiada, że prędkość (jako wielkość skalarna) jest stała. Dlatego wzór ten zachodzi też dla dowolnie długich odcinków czasowych:

Ze względu na tor, ruch jednostajny dzieli się na: Ruch jednostajny prostoliniowy, Ruch jednostajny krzywoliniowy Ruch jednostajny po okręgu

W każdym rodzaju ruchu jednostajnego: przebyta droga jest proporcjonalna do czasu
.

prędkość jest stała
.

przyspieszenie w kierunku ruchu jest równe zeru.

przyspieszenie prostopadłe do kierunku ruchu (przyspieszenie dośrodkowe) jest równe:.

Przyspieszenie dośrodkowe w ruchu prostoliniowym jest równe zeru.

Gdzie:
- prędkość (szybkość) jako wielkość skalarna.

Ruch jednostajny prostoliniowy - ruch ze stałą prędkością i w stałym kierunku, którego torem jest linia prosta, opisywany wzorami:

gdzie: v - prędkość chwilowa
- prędkość średnia (szybkość)
- przemieszczenie s - droga t - czas

Ponieważ w ruchu prostoliniowym kierunek ruchu nie zmienia się, to:

kierunek i zwrot wektora prędkości jest stały i zgodny z kierunkiem i zwrotem ruchu,

wartość prędkości - stała

przyspieszenie jest równe zeru, ponieważ wektor prędkości jest stały

Ruch jednostajnie zmienny - ruch, w którym:

Jest to ogólny przypadek ruchu jednostajnie przyspieszonego (a>0) i opóźnionego (a<0).

Przemieszczenie
Jest to wielkość wektorowa. Znak przemieszczenia świadczy o tym, w którą stronę osi x przesunęło się ciało.
Prędkość średnia Jeśli ciało w czasie Δt przesunęło się o Δx to:
Znak tej wielkości wskazuje średni kierunek ruchu (jest to wielkość wektorowa). Jej wartość nie zależy od drogi, ale od przemieszczenia (więc od położenia początkowego i końcowego). Na wykresie x(t) jest ona równa nachyleniu prostej przechodzącej przez punkty na krzywej odpowiadającej początkowi i końcowi przedziału czasu.

Grawitacja nazywana czasami ciążeniem powszechnym to jedno z czterech oddziaływań podstawowych wyróżnianych przez fizykę. Oddziaływanie grawitacyjne jest zależne od masy posiadanej przez poszczególne ciała i od odległości między nimi.

Oddziaływanie grawitacyjne jest dużo słabsze niż oddziaływanie elektromagnetyczne, czy słabe albo silne w skalach odległości z którymi mamy do czynienia na co dzień. Jednak ciążenie jako jedyne może wpływać na ciała bardzo od siebie oddalone. Grawitacja jest oddziaływaniem, które sprawia, że obiekty astronomiczne tworzą się z rozrzedzonych obłoków gazu wypełniających Wszechświat. Ciążenie powoduje zapadanie się tych struktur i powstawanie galaktyk, gwiazd i planet. W codziennym życiu ciążenie objawia się nam w postaci przyspieszenia ziemskiego. Jabłka oraz inne przedmioty spadają, bo działa na nie grawitacja. W skali astronomicznej ciążenie wyjaśnia, dlaczego planety krążą wokół Słońca, a Księżyc dookoła Ziemi. Grawitacja zawsze powoduje przyciąganie, a nigdy odpychanie. Grawitacja może utrzymać w równowadze tak burzliwe procesy jak reakcje termojądrowe w jądrze Słońca. W szczególnym przypadku ciążenie może spowodować zapadanie się gwiazd i powstawanie czarnych dziur.

Ruch jednostajny po okręgu - ruch po torze o kształcie okręgu z prędkością o stałej wartości, tzn.
. Ruch jednostajny po okręgu jest ruchem niejednostajnie przyspieszonym, tzn. kierunek i zwrot wektorów przyspieszenia
i prędkości
zmieniają się cały czas w trakcie ruchu, nie zmieniają się natomiast ich wartości.

Ruch jednostajny po okręgu może być także definiowany jako ruch po okręgu ze stałą prędkością kątową

Ruch zmienny po okręgu - ruch po torze o kształcie okręgu ze zmienną wartością prędkości. W zależności od charakteru tej zmiany, można wyróżnić:

ruch jednostajnie zmienny po okręgu (wartość przyspieszenia kątowego jest stała)

ruch niejednostajnie zmienny po okręgu - wartość przyspieszenia kątowego opisana jest funkcją w czasie.

Siła dośrodkowa - w fizyce siła powodująca zakrzywianie toru ruchu ciała, skierowana wzdłuż normalnej (prostopadle) do toru, w stronę środka jego krzywizny. Wartość siły określa wzór:

gdzie:
- siła dośrodkowa,
- masa ciała,
- prędkość ciała,
- promień krzywizny toru ruchu. Siła dośrodkowa nie zmienia wartości prędkości ciała.

W ruchu po okręgu, powyższy wzór można wyrazić:

gdzie:
- prędkość kątowa w ruchu po okręgu.

Prędkość kątowa - w fizyce wielkość opisujaca ruch po okręgu (ruch obrotowy). Jest wektorem (pseudowektorem) leżącym na osi obrotu i skierowanym zgodnie z regułą śruby prawoskrętnej.

Jeśli współrzędna kątowa ciała określa kąt
to wartość prędkości kątowej
jest równa:

Jednostka prędkości kątowej w układzie SI to jeden radian przez sekundę.

Zależność chwilowej prędkości liniowej
ciała poruszającego się po okręgu o promieniu
od chwilowej prędkości kątowej
tego ciała dana jest wzorem:

W zapisie wektorowym zależność przyjmuje postać:

Przyspieszenie dośrodkowe (normalne) to przyspieszenie, którego doznaje ciało na skutek działania siły lub jej składowej prostopadłej do wektora prędkości ciała. W wyniku przyspieszenia normalnego ciało nie zmienia wartości prędkości lecz zmienia kierunek prędkości.

Zgodnie z II zasadą dynamiki:

gdzie: a_n - przyspieszenie normalne, F_n- składowa prostopadła do kierunku ruchu siły działającej na ciało, m - masa ciała.

Przykładem może być przyspieszenie wynikłe z działania siły grawitacji Słońca na Ziemię, Ziemi na satelitę.

W ruchu po okręgu o promieniu R przyspieszenie dośrodkowe wynosi:

lub w zapisie wektorowym:

gdzie v - prędkość ruchu po okręgu (w układzie SI w m/s) r - promień okręgu (w układzie SI w m) ω - prędkość kątowa
- wersor o kierunku promienia.

Przyspieszenie styczne Jest to składowa przyspieszenia styczna do toru ruchu, wpływająca na wartość prędkości. Stosując oznaczenie v dla wartości prędkości chwilowej i oznaczenie s dla drogi pokonanej przez ciało, przyspieszenie styczne as określają wzory:

Przyspieszenie kątowe Występuje w ruchu obrotowym - jest wektorem leżącym na osi obrotu i skierowanym zgodnie z regułą śruby prawoskrętnej. Jeśli współrzędną kątową ciała określa kąt α, a wartość prędkości kątowej oznaczymy jako ω, to wartość przyspieszenia kątowego ε wynosi:

Jednostka przyspieszenia kątowego w układzie SI to jeden radian przez sekundę do kwadratu.

Siła (
) jest wielkością wektorową miarą oddziaływań fizycznych między ciałami.

Jednostką siły w układzie SI jest niuton [N]. Nazwa tej jednostki pochodzi od nazwiska wybitnego fizyka Isaaca Newtona.

Siła ma wartość jednego niutona (1N) jeżeli masie 1 kilograma nadaje przyspieszenie 1 m/s² (metr na sekundę do kwadratu):

Siłę przedstawia, jako szybkość zmian pędu w czasie:

Przy stałej masie możemy wyjąć masę m przed nawias:

Szczególnym przypadkiem siły jest ciężar.

W układzie CGS jednostką siły jest dyna. Jednostką siły w układzie ciężarowym był kilogram siła [kG] lub kilopond kp. 1 kG, to siła, z jaką Ziemia przyciąga ciało o masie 1 kg. 1 kG (kilogram siły) to około 9,80665 N. Jednostkę tę można jeszcze spotkać w bardzo starych podręcznikach. Do oznaczania skrótu kilograma siły używano: kG, kp, kgf. Międzynarodowa organizacja miar zaleciła w 1955 roku przyjęcie skrótu kgf, wiele państw nie dostosowało się do tego zalecenia w tym i Polska. W Polsce używano kG, a w wielu krajach Europy używających nazwy kilopond stosowano kp. W 2005 roku rozporządzeniem ministra zalecono stosowanie kgf.

Istnieje propozycja, by w miejsce jednostki masy kilogram wprowadzić jednostkę graw i skrót G, wówczas skrót kG oznacza kilograw (obecna tona) i koliduje z przestarzałym obecnie skrótem jednostki siły kG.

Masa - w fizyce jedna z najważniejszych wielkości fizycznych określająca ich bezwładność (masa bezwładna) i oddziaływania grawitacyjne (masa grawitacyjna). Potocznie rozumiana jako ilość materii i energii zgromadzonej w ciele fizycznym.

W układzie jednostek miar SI wyrażana jest w kilogramach. Symbol stosowany na oznaczenie masy to: m.

Masa bezwładna Jest miarą bezwładności ciała, to znaczy przeciwdziałania się ciała zmianie ruchu wywołanej działaniem na nie siły. Według drugiej zasady dynamiki Newtona zachodzi równość:

gdzie: F - siła działająca na ciało, m - masa bezwładna ciała, v - prędkość ciała, t - czas. a - przyspieszenie

Powyższy wzór jest słuszny w mechanice nierelatywistycznej.

Masa grawitacyjna W mechanice nierelatywistycznej, wielkość opisująca oddziaływania grawitacyjne dwóch punktowych ciał występująca we wzorze na oddziaływania grawitacyjne:

gdzie: F - siła oddziaływania ciał, G - stała grawitacji, m₁, m₂ - masy oddziałujących ciał, r - odległości ciał.

W fizyce relatywistycznej pojęcie masy zależy od teorii, różne podejścia do masy przedstawiają szczególna teoria względności i ogólna teoria względności.

Jednym z postulatów ogólnej teorii względności jest zasada równoważności mówiąca że nie można rozróżnić spadku swobodnego od ruchu jednostajnego, z postulatu tego wynika, że te dwa rodzaje masy (bezwładna i grawitacyjna) są sobie równoważne.

Zgodnie z prawem zachowania masy - jeżeli układ nie wymienia materii z otoczeniem, to masa materii uczestniczącej w dowolnym procesie fizycznym lub chemicznym pozostaje stała. Jednak zgodnie z teorią względności Alberta Einsteina masa może być równoważnie postrzegana jako energia, i dlatego założenie pierwotne musi być rozszerzone na wszystkie rodzaje energii.

W szczególnej teorii względności masa jest wielkością skalarną i traktowana jest niezmienniczo, gdyż Autor teorii posługiwał się konsekwentnie pojęciem masy spoczynkowej. Słuszny jest w niej związek pomiędzy energią, pędem i masą ciała:

Czasem spotyka się też pojęcie "masy relatywistycznej",

Pęd - w mechanice wielkość fizyczna opisująca ruch ciała. Pęd mają wszystkie formy materii, np. ciała obdarzone masą, pole elektromagnetyczne, pole grawitacyjne.

Pęd w mechanice klasycznej [edytuj] Pęd punktu materialnego [edytuj] Pęd punktu materialnego jest równy iloczynowi masy [m] i prędkości [v] punktu. Pęd jest wielkością wektorową; kierunek i zwrot pędu jest zgodny z kierunkiem i zwrotem prędkości.

W układzie SI jednostka pędu nie ma odrębnej nazwy, a jest określana za pomocą jednostek prostszych, np. niuton·sekunda (N·s) lub kilogram·metr/sekunda (kg·m/s).

Zasada zachowania pędu [edytuj]

Zmiana pędu następuje w wyniku działania na ciało siły przez pewien czas. Iloczyn siły i czasu jej działania nazywany jest popędem siły (I).

Jeżeli w układzie inercjalnym na ciało (układ ciał) nie działa siła, lub działające siły równoważą się:

,

to całkowity pęd ciała (układu ciał) nie zmienia się:

Prawo zachowania pędu jest konsekwencją symetrii translacji w przestrzeni (twierdzenie Noether)

Jeżeli energia potencjalna jest niezmiennicza ze względu na translację,

to

czyli na ciało nie działa żadna siła i w konsekwencji pęd układu jest zachowany.

Popęd zwany też impuls i popęd siły jest wektorową wielkością fizyczną równą iloczynowi siły i czasu jej działania:

Dla siły zmieniającej się wzór ten można wyrazić:

gdzie I popęd siły F, F siła, t czas.

Jednostką popędu jest N·s = kg·m/s zwany czasami Huygens i oznaczany przez Hy.

Zasada zachowania pędu mówi, że dla dowolnego izolowanego układu punktów materialnych, bez względu na to, jakie jest oddziaływanie między nimi, suma wektorowa wszystkich pędów pozostaje stała. Przejawem działania tej zasady jest zjawisko odrzutu, polegające na tym, że przy rozpadzie ciała na dwie części obie otrzymują pędy jednakowe co do wartości bezwzględnej, lecz przeciwnie skierowane względem układu odniesienia, w którym ciało przed rozpadem pozostawało w spoczynku. Przykładem mogą być odrzuty przy strzelaniu z broni palnej, przy emisji cząsteczek z jądra atomowego itp. Na tej podstawie działają też samoloty odrzutowe oraz rakiety, gdzie pęd strumienia gazów wyrzucanych z dyszy nadaje samolotowi lub rakiecie pęd w kierunku przeciwnym.

Matematyczne sformułowanie zasady zachowania pędu:

Zasada nie dotyczy układów nie-izolowanych.

Zasada jest zawsze spełniona (dla dowolnego układu izolowanego) w każdym procesie fizycznym, tylko w niektórych zjawiskach opisywanych przez mechanikę kwantową możliwe jest krótkotrwałe jej złamanie (w czasie zajścia oddziaływania), jednak już po bardzo krótkim czasie (potrzebnym światłu na przebycie odległości między cząstkowych) zasada ta jest spełniona. Zasadę zachowania momentu pędu można wraz z zasadą zachowania materii-energii połączyć w zasadę zachowania czteropędu.

Zasada wynika z niezmienniczości lagranżjanu (hamiltonianu) względem przesunięć w przestrzeni (jeśli wszystkie punkty przesuniemy w przestrzeni o
to nowy układ będzie identyczny z pierwotnym). Sytuacji takiej odpowiada brak członu potencjalnego w lagranżjanie (hamiltonianie).

Zderzenie sprężyste, zderzenie elastyczne, jest to zderzenie, w którym w stanie końcowym mamy te same cząstki (obiekty) co w stanie początkowym i zachowana jest energia kinetyczna. Przykładami zderzeń sprężystych mogą być: przejście komety poruszającej się z prędkością hiperboliczną w okolicy słońca, z odchyleniem jej toru, czy rozproszenie niskoenergetycznej cząstki alfa na jądrze atomowym (eksperyment Rutherforda). Często stosowane jako przykład zderzenie sztywnych stalowych kul jest natomiast tylko w przybliżeniu zderzeniem sprężystym, niewielka część energii kinetycznej jest bowiem zawsze tracona w formie ciepła i fali akustycznej wyzwolonych w chwili zderzenia.

Zderzenie całkowicie niesprężyste, zderzenie doskonale nieelastyczne - zderzenie, w którym następuje największa możliwa strata energii kinetycznej, tj. zderzenie, którego produkty mają najmniejszą możliwą energię kinetyczną umożliwiającą im spełnienie zasady zachowania pędu.

Szczególnie łatwo jest analizować takie zderzenie w układzie środka masy zderzających się obiektów. W układzie tym całkowity pęd wynosi zero. Oznacza to, że minimalna energia kinetyczna po zderzeniu też może być zerowa, sytuacja ta odpowiada stanowi spoczynku wszystkich produktów zderzenia. Ponieważ jednak strata energii nie może zależeć od układu odniesienia, dochodzimy do wniosku, że w dowolnym układzie odniesienia wszystkie produkty zderzenia całkowicie niesprężystego poruszają się z tą samą prędkością w tym samym kierunku. Dla zderzeń obiektów makroskopowych oznacza to normalnie, że zderzające się ciała "sklejają się" i kontynuują ruch jako jeden obiekt. Energia kinetyczna ulega przy tym zamianie na odkształcenie i ciepło.

Relatywistyczne efekt Dopplera — efekt Dopplera zachodzący przy prędkościach bliskich prędkości światła w próżni. Podobnie jak w mechanice klasycznej relatywistyczny efekt Dopplera prowadzi do zmiany częstotliwości fali elektromagnetycznej mierzonej przez obserwatora. Aby zgodnie z mechaniką relatywistyczną obliczyć taką zmianę konieczne jest uwzględnienie przewidywanych przez szczególną teorię względności efektów takich jak dylatacja czasu. Będąc w stanie spoczynku w układzie współrzędnych porównawszy wskazania zegara pozostającego w tym samym nieruchomym układzie ze wskazaniami poruszającego się zegara, stwierdzimy, że zegar w ruchu chodzi wolniej (ΔT > Δt). Zjawisko takie nazywane jest dylatacją czasu.

Jeżeli kolejne wskazania zegarów odmierzają równe odstępy czasu, to uczynienie odwrotności lewej i prawej strony równania (1) poda związek pomiędzy obserwowaną częstotliwością własną :
„tyknięć" zegara i obserwowaną częstotliwością „tyknięć" zegara w ruchu:

Ten relatywistyczny efekt modyfikacji częstotliwości nosi nazwę efektu Dopplera drugiego rzędu lub relatywistycznego efektu Dopplera

Równoważność masy i energii jest jednym z najważniejszych wniosków ze szczególnej teorii względności. Wyraża się on przez jeden z najsłynniejszych wzorów w historii ludzkości:

gdzie: E - Energia m - masa, c - prędkość światła w próżni.

Wzór ten mówi, że energia każdego ciała jest równoważna jego masie. Wielkość tej energii w ustalonych jednostkach to wartość masy w tych jednostkach pomnożona przez prędkość światła do kwadratu. Prędkość światła jest tylko współczynnikiem przeliczania masy na energię, w odpowiednio dobranym układzie jednostek miar np. (Jednostki naturalne) w którym prędkość światła jest bezwymiarowa i równa 1, masa jest równa energii.

Zasada zachowania energii - w układzie izolowanym suma składników wszystkich rodzajów energii całości (suma energii wszystkich jego części) układu jest stała (nie zmienia się w czasie).

Zasadę zachowania energii mechanicznej w formie zbliżonej do współczesnej sformułował Julius Robert von Mayer w roku 1842 przebywając w okolicach Jawy.

Zasada zachowania energii w mechanice klasycznej i kwantowej jest konsekwencją symetrii translacji (przesunięć) w czasie. Ma ona jednak w fizyce szersze znaczenie. Przyjmuje się, że zasada zachowania energii jest spełniona również w układach nieprzejawiających takiej symetrii i nie dających się opisywać przy użyciu formalizmu hamiltonowskiego. W ramach tego formalizmu wyprowadzany jest związek między zasadami zachowania a symetriami układów fizycznych. Przykładami takich układów są:

układy opisywane przez fizykę statystyczną, gdzie symetria w czasie dla całego układu nie jest zachowana,

układy związane z występowaniem siły tarcia,

inne układy na przykład cechujące się przemianami nierównowagowymi, dla których opis hamiltonowski jest nieadekwatny.

W mechanice klasycznej jeżeli równania ruchu są niezmiennicze ze względu na przesunięcia w czasie

to siła F lub potencjał U nie może jawnie zależeć od czasu

Konsekwencją równań Hamiltona (patrz mechanika klasyczna) jest stałość energii(hamiltonianu), bo:

Tak więc zachowana jest wielkość

Symetria translacji w czasie jest szczególnym przypadkiem ogólniejszej symetrii związanej z niezmienniczością mechaniki klasycznej względem transformacji Galileusza

Transformacje te tworzą grupę Galileusza. W szczególnej teorii względności zachowanie energii jest również konsekwencją translacji w czasoprzestrzeni Minkowskiego

Pamietając, że x⁰ = ct, przypadek dla μ=0 odpowiada translacji czasu.

Konsekwencją symetrii translacji w czasoprzestrzeni Minkowskiego jest zachowanie tensora energii - pędu.

Z zasady zachowania energii wynika kilka innych zasad między innymi: Pierwsza zasada termodynamiki, zasada zachowania energii mechanicznej.

Pierwsza zasada termodynamiki to prosta zasada zachowania energii, czyli ogólna reguła głosząca, że energia w żadnym procesie nie może pojawić się "znikąd".

Zmiana energii wewnętrznej układu ΔU = ΔQ + W

Istnieją różne sformułowania tej zasady, zależnie od sytuacji:

Sformułowanie najbardziej ogólne:
Energia wewnętrzna układu zamkniętego nie zmienia się, niezależnie od przemian zachodzących w tym układzie.

Sformułowanie dla procesów cieplno-mechanicznych:
Zmiana energii wewnętrznej układu jest równa sumie pracy wykonanej przez układ bądź nad układem i ciepła dostarczonego lub oddanego przez układ.

Doświadczalną podstawą pierwszej zasady jest doświadczenie Joule'a i pokrewne mu, które dowodzą równoważności ciepła i pracy mechanicznej przez pokazanie możliwości całkowitej zamiany pracy na ciepło. Uznanie ciepła jako innego niż praca sposobu zmiany energii prowadzi w naturalny sposób do włączenie ciepła do zasady zachowania energii. Pierwsza zasada termodynamiki jest dokładnie tym prawem.

Joule, Mayer (1842), Helmholtz (1847): Zmiana energii wewnętrznej układu równa jest dostarczonemu do układu ciepłu i pracy wykonanej nad układem przez siły zewnętrzne:

ΔU = W + ΔQ

Gdzie: ΔU - zmiana energii wewnętrznej układu ΔQ - ciepło wymienione przez układ z otoczeniem, jeśli układ oddaje ciepło, jego energia wewnętrzna maleje W - praca wykonana przez układ lub nad układem

Pierwsza zasada termodynamiki pozwala na zdefiniowanie energii wewnętrznej jako funkcji stanu: dla wszystkich procesów prowadzących od pewnego określonego stanu do drugiego, zmiana ΔU ma zawsze tę samą wartość, choć ilości dostarczanego ciepła i wykonanej pracy są na ogół różne dla różnych procesów. W warunkach nieskończenie małych przyrostów, pierwsza zasada termodynamiki jest w tym przypadku wyrażona następująco:

gdzie δQ i δW są "różniczkami niezupełnymi", tj. zależnymi od drogi; dU zaś jest "różniczką zupełną", tj. niezależną od sposobu przebiegu procesu.

Ruch obrotowy to taki ruch, w którym wszystkie punkty bryły sztywnej poruszają się po okręgach o środkach leżących na jednej prostej zwanej osią obrotu. Np. ruch Ziemi wokół własnej osi. Jest to ruch złożony z ruchu postępowego środka masy danego ciała oraz ruchu obrotowego względem pewnej osi. Środek masy ciała można uważać za punkt materialny. Do opisania ruchu obrotowego używa się odmiennych pojęć od używanych do opisania ruchu postępowego.

Podstawowym prawem opisującym ruch bryły sztywnej jest druga zasada dynamiki ruchu obrotowego:

gdzie M jest momentem siły względem obranego punktu odniesienia, a L - krętem względem tego samego punktu odniesienia.

Jeżeli obrót odbywa się względem osi stałej lub sztywnej wówczas druga zasada dynamiki dla ruchu obrotowego może być napisana w następujący sposób:

gdzie M oznacza moment siły a I moment bezwładności względem osi obrotu.

Czasem ta sama siła może powodować ruch postępowy i obrotowy. Wówczas dzieląc obie strony poprzedniego równania przez r oraz dodając po prawej stronie wyraz odnoszący się do ruchu postępowego można otrzymać II zasadę dynamiki w postaci bardziej ogólnej:

Gdy brak momentu sił zewnętrznych (M = 0), z równania
otrzymać można zasadę zachowania krętu:

L = Iω = const Moment bezwładności I punktu materialnego o masie m znajdującego się w odległości r od osi obrotu wyraża się wzorem: I = mr² Pierwsza zasada dynamiki ruchu obrotowego: W inercjalnym układzie odniesienia bryła nie obraca się lub obraca się ruchem jednostajnym (ω = const), gdy nie działają na nie żadne momenty sił lub gdy działające momenty sił się wzajemnie równoważą.

Moment bezwładności to miara bezwładności ciała w ruchu obrotowym. Im większy moment, tym trudniej zmienić ruch obrotowy ciała, np. rozkręcić dane ciało lub zmniejszyć jego prędkość obrotową.

gdzie:

m - masa fragmentów ciała oddalonych od osi obrotu o długość r

r - odległość fragmentów ciała od jego osi obrotu

Iloczyn
jest momentem bezwładności elementu ciała. Moment bezwładności ciała zależy od wyboru osi obrotu, od kształtu ciała i od rozmieszczenia masy w ciele. Moment bezwładności ma wymiar ML². Zwykle mierzy się go w kgm² . Posługując się pojęciem momentu bezwładności można wyrazić energię kinetyczną obracającego się ciała sztywnego w postaci

Dla ciał o ciągłym rozkładzie masy sumowanie we wzorze na moment bezwładności przechodzi w całkowanie. Niech ciało będzie podzielone na nieskończenie małe elementy o masach dm, oraz niech r oznacza odległość każdego takiego elementu od osi obrotu. W takim przypadku moment bezwładności określa wzór:

gdzie całkowanie odbywa się po całej objętości ciała

Moment siły (moment obrotowy) -
siły
względem punktu O jest iloczyn wektorowy promienia wodzącego
, o początku w punkcie O i końcu w punkcie przyłożenia siły oraz siły
:

Wektor momentu siły jest wektorem osiowym (pseudowektorem), zaczepiony jest w punkcie O, a jego kierunek jest prostopadły do kierunku płaszczyzny wyznaczonej przez wektory
i
.

Określa się także moment siły względem osi, jest on równy rzutowi wektora momentu siły na tę prostą. Współrzędne M_x, M_y i M_z wektora
nazywają się momentami siły względem odpowiednich osi x, y i z. Jednostką momentu siły jest
. Jednostka ta jest zdefiniowana analogicznie, jak dżul, czyli jednostka energii. Aby nie tworzyć nieporozumień, nie sprowadza się niutonometra do dżula.

W przypadku wagi szalkowej, o nierównych ramionach, waga pozostanie w równowadze, gdy wartości momentów sił przyłożone do obu ramion będą równe, a ściślej, gdy suma wektorów momentów będzie równa zeru:

Jeżeli jedna z sił jest ciężarem jakiegoś ciała, a druga jest siłą wymuszaną, układ z powyższego rysunku nazywany jest dźwignią dwuramienną (dwustronną).

Archimedes użył słów: "Dajcie mi dostatecznie długą dzwignię i punkt podparcia, a poruszę Ziemię". Pragnął więc użyć dźwigni, na której końcu umieściłby naszą planetę, zaś na drugim, odpowiednio długim ramieniu, mógłby przyłożyć niewielką siłę. Pomijając fakt, że dźwignia taka musiałaby być niezwykle długa, to brakowało mu właśnie punktu podparcia.

Zasady dynamiki ruchu obrotowego II zasada dynamiki ruchu obrotowego

Rozwa_my znów przykład ciała obracajacego sie wokół ustalonej osi. Dzielimy je w myslach na bardzo małe elementy (masy punktowe), które numerujemy wskaznikiem i. Załó_my, _e na i-ta mase punktowa (mi) działa siła o wartosci Fi, le_aca w płaszczyznie prostopadłej do osi obrotu i odległa od tej osi o ri : Ograniczmy sie znów do szczególnego przypadku ustalonej osi obrotu; wtedy istotna jest tylko składowa momentu siły równoległa do osi obrotu: Mos = M. Wartosc momentu siły (liczonego wzgledem osi obrotu) działajacego na mase mi wynosi: Mi=Firi. Momenty sił pochodzace od poszczególnych elementów mi sa równoległe i dodaja sie. Wartość całkowitego momentu siły wynosi:M= ΣFr=Σafr gdzie ai jest przyspieszeniem (ruchu postepowego) masy mi. Wykorzystujac relacje pomiedzy przyspieszeniami ruchu postepowego i ruchu obrotowego: ai = ri , zwiazek powy_szy mo_na przepisac: Rezultat ten mo_na przepisac w wektorowej postaci: M  I (relacja powyższa jest prawdziwa w takiej prostej formie jesli moment siły M jest liczony względem ustalonej osi obrotu; oznacza to, _e bierzemy składowa momentu pedu równoległa do osi obrotu). Mówilismy ju_ o tym, _e moment pedu ciała (liczony wzgledem ustalonej osi obrotu) wynosi ; z porównania tego rezultatu z Równ. 60 otrzymujemy: M  dl:dt Wynik ten dostalismy dla szczególnego przypadku ruchu obrotowego wokół ustalonej osi. Niemniej rezultat ten jest prawdziwy dla dowolnego ruchu obrotowego. Równanie powy_sze wyra_a II zasade dynamiki dla ruchu obrotowego. Mówi ona, _e: Jesli na ciało działa moment siły M to powoduje on zmiane momentu pedu dL/dt=M. Pozostaje ona w pełnej analogii z druga zasada dynamiki dla ruchu postepowego, która mo_emy wyrazic jako: F=dp/dt.

Zasada zachowania momentu pedu (I zasada dynamiki ruchu obrotowego)

Z drugiej zasady dynamiki: M=dL/dt (lub: dL=Mdt) wynika, _e jesli moment siły jest zerowy, to przyrost momentu pedu tak_e jest zerowy. W oparciu o powy_sze formułujemy zasade zachowania momentu pedu: Jesli na ciało nie działa moment siły (M=0), to moment pedu ciała jest stały (L=const). Zasada zachowania momentu pedu jest równowa_na I zasadzie dynamiki ruchu

obrotowego.

III zasada dynamiki ruchu obrotowego Podobnie jak siły, momenty sił równie_ wystepuja parami. Mo_emy zatem sformułowac zasade akcji i reakcji dla momentów sił: Jesli ciało A działa na ciało B momentem siły MAB, to równoczesnie ciało B działa na A

momentem siły MBA, przy czym MAB= - MBA.

Zestawienie wielkości kinetycznych i dynamicznych w ruchu postępowym i obrotowym

Ruch postępowy Ruch obrotowy

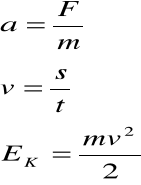
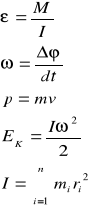
Pole grawitacyjne to pole wytwarzane przez obiekty posiadające masę. Określa wielkość i kierunek siły grawitacyjnej działającej na znajdujące się w nim inne obiekty posiadające masę. Podstawową teorią opisującą pole grawitacyjne i jego związek z cechami przestrzeni jest ogólna teoria względności, stworzona przez Alberta Einsteina.

Pole opisuje się poprzez podanie natężenia pola grawitacyjnego g, czyli siły F działającej na masę jednostkową m , lub potencjału grawitacyjnego. Obrazem pola grawitacyjnego są linie pola lub powierzchnie ekwipotencjalne. Kierunek i zwrot linii pola jest zgodny z kierunkiem i zwrotem sił działających na masę punktową.

Pole grawitacyjne punktu lub jednorodnej kuli jest polem centralnym, ale w odniesieniu do małej przestrzeni w porównaniu do odległości centrum grawitacji to pole może być uznane za jednorodne.

Pole grawitacyjne jest bezpośrednio sprzężone z przestrzenią i wpływa na jej parametry- zakrzywia przestrzeń. Z wielkości zakrzywienia czasoprzestrzeni można wyznaczyć parametry źródła pola grawitacyjnego tj. masa lub gęstość energii, jak i na odwrót.

Blisko powierzchni źródła pola, natężenie pola grawitacyjnego jest równe przyśpieszeniu grawitacyjnemu.

Natężeniem pola grawitacyjnego nazywamy stosunek siły grawitacyjnej działającej na ciało, do masy tego ciała. Natężenie pola grawitacyjnego jest polem wektorowym, które podlega prawu Gaussa:

gdzie: m - masa ciała "próbnego"; F - siła jaka działa na ciało "próbne" .

Natężenie pola grawitacyjnego wytwarzane przez punktową masę w odległości r od masy:

Natężenie pola jest równe przyspieszeniu grawitacyjnemu w tym punkcie (przyspieszenie grawitacyjne dla Ziemi nazywamy przyspieszeniem ziemskim), zatem:

Pole grawitacyjne jest polem potencjalnym. praca wykonywana w tym polu nie zależy od drogi po jakiej przemieszczają się ciała, tylko od różnicy potencjałów w punkcie początkowym i końcowym. Możliwe jest zatem zdefiniowanie funkcji U, która opisuje potencjał pola grawitacyjnego. Spełnia ona następującą zależność:

Korzystając z tego równania można obliczyć energię potencjalną pola grawitacyjnego

Potencjał w fizyce to wielkość fizyczna zwykle o wymiarze energii lub napięcia elektrycznego przypisana punktowi w przestrzeni. Znane są także przykłady pól fizycznych, określanych za pomocą potencjału wektorowego. Dla potencjałów skalarnych różnica potencjałów określa ilość energii koniecznej do przemieszczenia ciała z jednego punktu do drugiego. Potencjał wiąże się bezpośrednio z polem potencjalnym.

Ścisła definicja: potencjał to forma określona na przestrzeni w której opisujemy rozważane zjawiska o wartościach rzeczywistych lub zespolonych, której pochodna zewnętrzna jest równa natężeniu pola fizycznego. Kluczowe znaczenie w teorii potencjału ma twierdzenie Stokesa. Potencjały w ogólnym sensie przynależą nie tylko do teorii pola, ale są również podstawą ogólnego sformułowania termodynamiki fenomenologicznej.

Pole potencjalne to takie, dla którego ilość energii koniecznej do przemieszczenia ciała z jednego punktu do drugiego nie zależy od drogi. Pole potencjalne jest zwykłe opisane poprzez wektor siły określony dla każdego punktu przez funkcję wektorową. Rotacja pola potencjalnego jest równa zero:

Powierzchnia ekwipotencjalna - (powierzchnia równego potencjału) powierzchnia w polu potencjalnym, której wszystkie punkty mają jednakowy potencjał.

Powierzchnie potencjalne określa się dla wszystkich pól potencjalnych np. pola elektrostatycznego, pola grawitacyjnego.

Powierzchnie ekwipotencjalne są w każdym punkcie pola prostopadłe do wektora siły, czyli do linii natężenia pola.

W przypadku pola centralnego, np pole elektryczne ładunku punktowego, pole grawitacyjne masy punktowej są to współśrodkowe sfery. W przypadku pola jednorodnego, np pole elektryczne między okładkami kondensatora,są to równoległe płaszczyzny.

Prawo powszechnego ciążenia Dnia 5 czerwca roku 1686 Izaak Newton wydał dzieło, w którym przedstawił spójną teorię grawitacji opisującą zarówno spadanie obiektów na ziemi, jak i ruch ciał niebieskich. Angielski fizyk oparł się na zaproponowanych przez siebie zasadach dynamiki oraz prawach Keplera dotyczących odległości planety od Słońca.

Dla uproszczenia załóżmy, że dwie planety poruszają się po kołowej orbicie. Prawo Keplera przyjmie dla nich postać:

gdzie: R₁,R₂ - promienie orbit, T₁, T₂ - okresy obiegu planet.

Zgodnie z rachunkiem wektorowym ciało poruszające się po okręgu jest poddane przyspieszeniu:

gdzie: a - przyspieszenie, v - prędkość, R - promień okręgu, co według drugiej zasady dynamiki oznacza, że musi działać na nie siła dośrodkowa:

gdzie m_b to masa bezwładnościowa ciała. Przy ruchu planet ta siła dośrodkowa jest równa sile grawitacyjnej F_g. Prędkość orbitalna może być wyliczona jako:

Jeżeli podstawimy zależność (4) do (3) to otrzymamy:

Stosunek sił grawitacyjnych dla planet można rozpisać jako:

Jeżeli teraz do równania (5) podstawimy (1) to pozbędziemy się okresów obiegu:

Otrzymana zależność oznacza tyle, że stosunek sił grawitacyjnych jest proporcjonalny do odwrotności stosunku kwadratów odległości. Jeżeli planeta jest dwa razy dalej od Słońca, to siła grawitacji jest cztery razy mniejsza. Kiedy ciało ma dwa razy mniejszą masę, wtedy siła jest dwa razy mniejsza.

Newton uznał, że ta sama siła powoduje ruch planet po orbitach oraz spadanie jabłka z drzewa. W ten sposób ten wielki fizyk położył podwaliny pod mechanikę klasyczną. W tym ujęciu grawitacja jest siłą, z jaką oddziałują na siebie wszelkie ciała obdarzone masą.

Prawo powszechnego ciążenia głosi, że: między dowolną parą ciał posiadających masy pojawia się siła przyciągająca, która działa na linii łączącej ich środki, a jej wartość rośnie z iloczynem ich mas i maleje z kwadratem odległości.

Pole grawitacyjne jest polem potencjalnym. praca wykonywana w tym polu nie zależy od drogi po jakiej przemieszczają się ciała, tylko od różnicy potencjałów w punkcie początkowym i końcowym. Możliwe jest zatem zdefiniowanie funkcji U, która opisuje potencjał pola grawitacyjnego. Spełnia ona następującą zależność:

Korzystając z tego równania można obliczyć energię potencjalną pola grawitacyjnego.

Grawitacja na powierzchni Ziemi Kiedy znajdujemy się na powierzchni naszej planety, odległość od środka ciężkości Ziemi jest dużo większa niż wysokość, na której możemy się przemieszczać (bez rakiet). W takiej sytuacji można założyć, że pole grawitacyjne jest jednorodne. Korzystając z zależności na siłę grawitacyjną można obliczyć, że przedmiot o masie m na powierzchni naszej planety działa siła F_g:

gdzie M_z ≈ 5,9736×10²⁴ kg - masa Ziemi, r_z ≈ 6373,14 km , a zgodnie z drugą zasadą dynamiki:

Podstawiając zależność na siłę można obliczyć przyspieszenie ziemskie g:

W praktyce wartość przyspieszenia ziemskiego zależy od wielu czynników. Umowna wartość g (dodaje się indeks "n" w celu zaznaczenia, że jest to przyspieszenie "normalne") to:

Spadający człowiek porusza się z przyspieszeniem ziemskim tylko przez kilka sekund. Potem opór powietrza staje się na tyle znaczący, że równoważy siłę grawitacji. Punkt równowagi odpowiada zwykle 200 km/h. Spadochron zwiększa siłę oporu powietrza i prędkość odpadania stabilizuje się na dużo mniejszej wartości.

Na Księżycu brak atmosfery powoduje, że wszystkie ciała spadają z takim samym przyspieszeniem. Podczas lotów programu Apollo astronauci przeprowadzili pokazy ze zrzucaniem różnych przedmiotów, które transmitowała telewizja. Brak atmosfery hamującej ruch pojazdu powoduje, że lądowanie na Srebrnym Globie wymaga dużych ilości paliwa rakietowego. Spadochrony w próżni nie są skuteczne.

Przyspieszenie ziemskie - przyspieszenie grawitacyjne ciał swobodnie spadających na Ziemię, bez oporów ruchu. Wartość przyspieszenia ziemskiego zależy od szerokości geograficznej oraz wysokości nad poziomem morza. Nie obserwuje się zależności przyspieszenia ziemskiego od długości geograficznej.

Przyspieszenie ziemskie normalne (na szerokości geograficznej 45° i poziomie morza) wynosi

Układ inercjalny - układ odniesienia, względem którego każde ciało niepodlegające zewnętrznemu oddziaływaniu z czymkolwiek porusza się bez przyspieszenia (tzn. ruchem jednostajnym prostoliniowym); zwany również układem "inercyjnym". Istnienie takiego układu jest postulowane przez pierwszą zasadę dynamiki Newtona. Zgodnie z zasadą względności Galileusza wszystkie inercjalne układy odniesienia są równouprawnione i wszystkie prawa mechaniki są w nich identyczne. Identyczne są również wszystkie prawa fizyki w układach inercjalnych. Uogólnienie tej zasady na układy nieinercjalne jest podstawową treścią ogólnej teorii względności.

Ziemię przyjmuje się często za układ inercjalny. W rzeczywistości, układ związany z Ziemią nie jest inercjalny ponieważ w związku z jej ruchem obrotowym, na ciała materialne znajdujące się na jej powierzchni, działają siły bezwładności: siła odśrodkowa oraz siła Coriolisa. Lepszym przybliżeniem układu inercjalnego jest układ związany ze Słońcem.

Nieinercjalny układ odniesienia - układ odniesienia poruszający się ruchem niejednostajnym względem jakiegokolwiek inercjalnego układu odniesienia.

Transformacja równań ruchu z układu inercjalnego do układu nieinercjalnego powoduje, że w równaniu ruchu zapisanym w układzie nieinercjalnym pojawiają się dodatkowe wyrazy, których wartość zależy od ruchu układu nieinercjalnego względem inercjalnego. Wyrazy te mają wymiar siły i dlatego mówimy, że w takim układzie występują pozorne siły. Przykładem takich sił jest siła bezwładności i siła Coriolisa.

Ciężar, siła ciężkości - siła z jaką Ziemia lub inne ciało niebieskie przyciąga dane ciało. Ciężar jest wypadkową sił przyciągania, grawitacyjnego i siły odśrodkowej wynikającej z ruchu obrotowego określonego ciała niebieskiego.

Jakkolwiek teoretycznie pole grawitacyjne każdego ciała niebieskiego rozciąga się na cały Wszechświat, zazwyczaj mówiąc o ciężarze ma się na myśli układ planety i ciała znajdującego się stosunkowo blisko jej powierzchni. W przypadku Ziemi ciężar ciała zależy od położenia ciała względem Ziemi, zależny jest między innymi od szerokości geograficznej, wysokości nad poziomem morza i budowy podłoża.

Jednostką ciężaru w układzie SI jest niuton, jednak nadal dozwolone jest używanie jednostek spoza układu SI - stosuje się jeszcze np. kilogram-siłę - kG (kilogram siła).

Ciężar, jako siła, jest wielkością wektorową - wektor ciężaru skierowany jest w każdym miejscu do środka ciężkości układu planeta-ciało, co w praktyce oznacza środek ciężkości planety.

Jeżeli masa sferycznie symetrycznej planety o promieniu r wynosi M, a masa danego ciała m, to wartość ciężaru ciała na powierzchni planety dana jest wzorem:

gdzie G jest stałą grawitacji:

nazywa się przyspieszeniem grawitacyjnym na powierzchni planety i oznacza przez g, co prowadzi do prostego wzoru łączącego masę ciała z jego ciężarem:

F = m · g. Oznacza to, że przy ustalonym g ciężar jest proporcjonalny do masy ciała.

Dla Ziemi g ≈ 9,81 m/s². W przypadku Księżyca: g_K ≈ 1,62 m/s², co oznacza, że ciężar każdego ciała jest tam około sześciokrotnie mniejszy niż na Ziemi.

W potocznym myśleniu nie rozróżnia się masy i ciężaru, stosując te dwa pojęcia wymiennie (często używa się wtedy też słowa waga).

Tarcie (pojęcie fizyczne) (opory ruchu) to całość zjawisk fizycznych towarzyszących przemieszczaniu się względem siebie dwóch ciał fizycznych (tarcie zewnętrzne) lub elementów tego samego ciała (tarcie wewnętrzne) i powodujących rozpraszanie energii podczas ruchu.

Tarcie zewnętrzne występuje na granicy dwóch ciał stałych. Tarcie wewnętrzne występuje przy przepływie płynów, jak i deformacji ciał stałych, pomiędzy obszarami przemieszczającymi się względem siebie.

Siła występująca w zjawiskach tarcia nazywana jest siłą tarcia.

Podstawowy podział tarcia:^[1] tarcie zewnętrzne tarcie ślizgowe tarcie spoczynkowe (tarcie statyczne) tarcie ruchowe (tarcie kinetyczne) tarcie toczne tarcie wewnętrzne

Podział stosowany w technice, uwzględniający występowanie środków smarnych: tarcie suche tarcie płynne tarcie graniczne tarcie mieszane

W tarciu zewnętrznym suchym, z zazwyczaj siła tarcia spoczynkowego jest większa lub równa sile tarcia ruchowego:
.

Choć zjawiska wywołujące tarcie mają skomplikowana naturę - od czysto mechanicznej po molekularną, matematyczny opis zjawiska jest bardzo prosty.

Jeżeli ciało nie porusza się, to siła tarcia statycznego równoważy siłę wypadkową pozostałych sił działających na ciało, ma jej kierunek, a zwrot przeciwny. Maksymalną wartość siły jaka może wystąpić określa wzór:

Jeżeli ciało porusza się, to siła tarcia dynamicznego ma kierunek ruchu ciała, zwrot przeciwny kierunkowi ruchu, wartość T jest równa:

Gdzie:
- współczynnik tarcia zależny od rodzaju powierzchni stykających się ciał

- siła nacisku N, siła prostopadła do powierzchni styku ciał.

Gdy ciało porusza się, tak że jego elementy stykające się z powierzchnią mają różne kierunki ruchu (np złożenie ruchu postępowego i obrotowego), to siły tarcia pochodzące od poszczególnych punktów styku ciała z podłożem mają różne kierunki.

Siły pozorne, czyli siły bezwładności lub siły bezźródłowe to pseudosiły, których efekty działania można obserwować tylko w obrębie układów nieinercjalnych - to znaczy układów poruszających się ze zmiennym wektorem prędkości. Najbardziej powszechne siły pozorne to: siła bezwładności w hamowaniu lub przyspieszaniu siła odśrodkowa siła Coriolisa

Siła bezwładności w hamowaniu lub przyspieszaniu pojawia się w układzie nieinercjalnym, poruszającym się ze zmienną wartością wektora prędkości. Najlepiej zrozumiemy jej istotę na przykładzie wagonu jadącego po prostych torach.
Obserwator umieszczony w przedziale wagonu, kładzie filiżankę z kawą na stoliku przed sobą. Inny obserwator stoi przy nasypie kolejowym (jest w układzie inercjalnym, bo możemy traktować nasyp jako spoczywający, czyli niezmieniający prędkości).
Na początku pociąg porusza się ruchem jednostajnym po linii prostej. Obserwator przy nasypie widzi filiżankę poruszającą się (wraz z wagonem) ze stałą prędkością. Obserwator w przedziale widzi, że filiżanka spoczywa w jego układzie odniesienia (względem ściany przedziału).

Z powyższego rysunku widzimy, że filiżanka zachowuje stałą odległość od ściany przedziału (spoczywa względem niej), bo porusza się w prawo dokładnie tak samo jak ścianka.
Nagle wagon hamuje, czyli zmienia prędkość. Staje się wtedy układem nieinercjalnym. Obserwator przy nasypie (układ inercjalny) widzi, że układ-wagon zahamował, a filiżanka porusza się nadal z tą samą prędkością, z jaką poruszała się (bezwładność). Obserwator ten nie widzi żadnej zmiany w zachowaniu filiżanki.
Obserwator wewnątrz przedziału (układ nieinercjalny) zobaczy, że w momencie hamowania pociągu filiżanka nagle „zrywa się” ze stolika i zaczyna podążać w kierunku ścianki przedziału, aby się o nią rozbić. Obserwator ten wyciągnie następujący wniosek: na filiżankę musiała zadziałać jakaś tajemnicza siła. Jest to właśnie siła bezwładności w hamowaniu.

Dlaczego jest ona pozorna? Bo tak naprawdę z filiżanką nic nowego się nie dzieje i tak właściwie to nie przyspieszająca filiżanka rozbija się o ściankę, ale hamująca ścianka „nadziewa się” na filiżankę. A dlaczego jest ona bezźródłowa? Bo za ścianką nie ma żadnego źródła siły bezwładności. Jest to pseudosiła, bo prawdziwe siły zawsze mają źródło (np. ładunek, masę).
Innym rodzajem siły pozornej jest siła odśrodkowa. Pojawia się ona we wszystkich układach nieinercjalnych, których tor ruchu ma krzywiznę (kierunek wektora prędkości zmienia się). Dla uproszczenia weźmy samochód poruszający się po okręgu. Będzie on naszym układem nieinercjalnym. Gdy samochód, który najpierw jechał ze stałą prędkością po linii prostej, zaczyna zataczać okrąg, to pasażer siedzący w środku „chce” dalej poruszać się po prostej (bezwładność). Dlatego „wpada” ona na boczne drzwi samochodu. Odczuwa on, że jakaś tajemnicza siła wyrzuca go na bok. Jest to właśnie siła odśrodkowa.
Obserwator obserwujący samochód z zewnątrz powie, że pasażer porusza się tak jak wcześniej i nic się z nim nie dzieje. To po prostu samochód zaczął skręcać i „nadział się” bocznymi drzwiami na pasażera.

Siła Coriolisa działa na każde ciało znajdujące się w obracającym się układzie nieinercjalnym, które wykonuje wewnątrz tego układu ruch. Jest jeszcze jeden warunek: wektor prędkości tego ruchu nie może być równoległy do wektora prędkości kątowej układu.
Wzór na wartość siły Coriolisa: F_c = 2m ωv sinα gdzie: F_c - siła Coriolisa, m - masa ciała, na które działa siła Coriolisa, ω - prędkość kątowa układu, v - prędkość ruchu ciała w obrębie układu, sinα - sinus kąta pomiędzy wektorem ω i wektorem v. Aby doznać działania tej siły na własnej skórze, najlepiej wejść na kręcącą się karuzelę i spróbować poruszać się w kierunku jej środka. Pojawi się siła powodującą skręt w bok podczas ruchu (prostopadła do ruchu). Jest to właśnie siła Coriolisa.

Ruch harmoniczny drgania opisane funkcją harmoniczną (sinusoidalną), jest to najprostszy w opisie matematycznym rodzaj drgań.

Ruch harmoniczny jest często spotykanym rodzajem drgań, wiele rodzajów jest w przybliżeniu harmoniczna. Każde drganie można przedstawić jako sumę drgań harmonicznych. Przekształceniem umożliwiającym rozkład ruchu drgającego na drgania harmoniczne jest transformacja Fouriera.

Ruch harmoniczny prost Każdy ruch powtarzający się w regularnych odstępach czasu nazywany jest ruchem okresowym. Jeżeli ruch ten opisywany jest sinusoidalną funkcją czasu to jest to ruch harmoniczny. Ciało porusza się ruchem harmonicznym prostym, jeżeli znajduje się tylko pod wpływem siły o wartości proporcjonalnej do wychylenia z położenia równowagi i skierowanej w stronę położenia równowagi (Prawo Hooke'a):

gdzie
- siła, k - współczynnik sprężystości,

- wychylenia z położenia równowagi.

Równanie ruchu (skalarne dla kierunku OX) dla takiego ciała można zapisać jako:

(Druga Zasada Dynamiki Newtona), w postaci różniczkowej:

Jest to równanie różniczkowe zwyczajne drugiego rzędu (występuje druga pochodna funkcji położenia x(t)).

Rozwiązania tego równania można równoważnie opisać za pomocą dowolnego z równań:

gdzie:

jest częstością kołową drgań,

stałe zależne od warunków początkowych.

Są to tzw. harmoniki. Rozwiązania są równoznaczne, a korzystając z tożsamości trygonometrycznych można znaleźć zależności pomiędzy powyższymi stałymi i rozwiązanie przedstawiać w dowolnej z postaci 1,2,3.

Częstość kołową ω₀ wiąże z Okresem drgań T związek:

,

częstotliwość drgań ν natomiast wynosi

Ważną własnością ruchu harmonicznego jest to, że inne wielkości (prędkość, przyspieszenie) też są opisane przez równanie harmoniczne. Energia w ruchu harmonicznym prostym

Energia potencjalna dla siły proporcjonalnej do wychylenia.

Z zasady zachowania energii, wynika zależność, z której można wyznaczyć energię kinetyczną:

Z równania powyższego wynika kilka faktów (na podstawie jedynki trygonometrycznej i porównania współczynników we wzorze
z powyższym):

Ciało drgajace ma maksymalną prędkość gdy przechodzi przez położenie równowagi i ma ona wartość: v₀ = x₀ω₀ prędkość chwilowa zmienia się jak

Bezpośrednio z równania ruchu wynika, że przyspieszenie jest opisywane zależnością:

Amplituda - nieujemna wartość określająca wielkość przebiegu funkcji okresowej

Amplituda A w przebiegach sinusoidalnych jest maksymalną wartością tego przebiegu:

(1)

W przypadku funkcji ze składową stałą, amplituda dotyczy tylko części sinusoidalnej:

Amplitudą w tym przypadku NIE JEST A+B, a tylko wartość A.

Uwaga 1: pojęcie amplitudy często jest mylone, jako różnica pomiędzy maksymalną a minimalną wartością przebiegu (czyli wg tego, wynosiłaby 2A)

Uwaga 2: Nieprawdziwe jest również definiowanie amplitudy jako wartość średnia z modułów maksymalnej i minimalnej wartości przebiegu (czyli
); taka definicja jest słuszna jedynie dla przebiegów symetrycznych np. sinusoidalnego z równania (1), gdyż wówczas | y_max | = | y_min | .

Pulsacja (częstość kołowa) - wielkość określająca, jak szybko powtarza się zjawisko okresowe. Pulsacja jest powiązana z częstotliwością (f) i okresem (T) poprzez następującą zależność:

2π - kąt pełny (2π radiana = 360 stopni)

Pulsacja jest stosowana najczęściej w technice do określania przebiegów sinusoidalnych i prędkości obrotowych. Zaletą używania pulsacji zamiast częstotliwości jest uproszczenie zapisu poprzez ukrycie symbolu π. Np. w równaniach drgań harmonicznych zamiast

a = − 4π²f²x mamy: a = − ω²x. W przypadku ruchu pulsacji odpowiada prędkość kątowa.

Częstotliwość określa liczbę cykli zjawiska okresowego występujących w jednostce czasu. W układzie SI jednostką częstotliwości jest herc (Hz). Częstotliwość 1 herca odpowiada występowaniu jednego zdarzenia (cyklu) w ciągu 1 sekundy. Najczęściej rozważa się częstotliwość drgań, częstotliwość napięcia, częstotliwość fali.

W fizyce częstotliwość oznacza się literą f lub grecką literą ν, a z innymi wielkościami wiążą ją następujące zależności:

, gdzie: T- okres, f - częstotliwość,

, gdzie: ω - pulsacja.

Albert Einstein zaproponował teorię fotonową, która wiąże z falą elektromagnetyczną o danej częstotliwości, pewien rodzaj cząstki zwanej fotonem, niosącej najmniejszy, niepodzielny kwant energii fali. Prowadzi to do zależności:

, gdzie: h - stała Plancka, E - energia kwantu, ν - częstotliwość fali.

Wahadło - ciało zawieszone lub zamocowane ponad swoim środkiem ciężkości wykonujące w pionowej płaszczyźnie drgania pod wpływem siły grawitacji. W teorii mechaniki rozróżnia się dwa podstawowe rodzaje wahadeł: matematyczne fizyczne

Wahadło matematyczne Punkt materialny zawieszony na nierozciągliwej i nieważkiej nici. Jest to idealizacja wahadła fizycznego. Ważną cechą wahadła fizycznego i matematycznego jest stałość okresu drgań dla niewielkich wychyleń wahadła. Ogólne równanie ruchu wahadła matematycznego:

Gdzie: l - długość nici, g - przyspieszenie ziemskie, m - masa ciała, θ - kąt wektora wodzącego ciała z pionem A - amplituda siły wymuszającej ω_D - częstość siły wymuszającej γ - współczynink oporu ośrodka

Wahadło fizyczne Bryła sztywna mogąca wykonywać obroty dookoła poziomej osi przechodzącej ponad środkiem ciężkości tej bryły.

Wzór na okres drgań wahadła fizycznego dla małych wychyleń:

Przez analogię do wahadła matematycznego wzór ten zapisuje się jako:

, wprowadzając wielkość długość zredukowana wahadła l₀

gdzie: d - odległość od punktu zawieszenia do środka ciężkości, g - przyspieszenie ziemskie, I - moment bezwładności ciała względem osi obrotu, m - masa ciała

Drgania - procesy, w trakcie których wielkości fizyczne na przemian rosną i maleją w czasie.

W zależności od rodzaju równań drgań wyróżnia się drgania liniowe i drgania nieliniowe.

Jeżeli na drgający układ ma wpływ inny drgający układ (siła wymuszająca) to drgania nazywa się wymuszonymi, gdy siła nie występuje drganiami swobodnymi. Układy autonomiczne (nie wymuszone) dzieli się na: zachowawcze (energia drgań nie zmienia się) tłumione (energia zmniejsza się) samowzbudne (energia drgań rośnie)

Rezonans mechaniczny to zjawisko polegające na przepływie energii pomiędzy kilkoma (najczęściej dwoma) układami drgającymi. Warunkami koniecznymi do zajścia rezonansu mechanicznego są: jednakowa częstotliwość drgań własnych (lub swobodnych) układów

istnienie mechanicznego połączenia między układami Przykładem układu, w którym występuje rezonans mechaniczny są wahadła sprzężone. Zjawisko to zachodzi gdy częstotliwość drgań wymuszających zbliża się do częstości drgań własnych. Gdy siła wymuszająca działa na drgające ciało z odpowiednią częstotliwością to amplituda drgań może osiągnąć bardzo dużą wielkość nawet przy niewielkiej sile wymuszającej.

Ze zjawiskiem rezonansu spotykamy się jadąc np. autobusem. Przy pewnej prędkości obrotów silnika szyby lub niektóre części karoserii zaczynają silnie drgać.

Rezonans ma decydujące znaczenie dla procesu wydobywania dźwięku w instrumentach muzycznych np.: - Wykorzystany jest w akustyce przy stosowaniu pudeł rezonansowych w rozmaitych instrumentach muzycznych. Np. : gitara. Gdy uderzymy strunę gitary do pudła rezonansowego wpada dźwięk uderzonej struny. W tym pudle dźwięk odbija się do jego ścianek wybrzmiewając dźwięk o częstotliwości drgań struny.

Drgania prostopadłe Kiedy drgania punktu materialnego odbywają się równocześnie w dwóch prostopadłych do siebie kierunkach, np. wzdłuż osi x i y prostokątnego układu współrzędnych, to wypadkowy ruch tego punktu na płaszczyźnie można opisać z pomocą równań postaci:

 gdzie j jest różnicą faz obu drgań składowych. Zwróćmy uwagę, że jeśli częstości drgań są jednakowe i różnica faz wynosi zero lub p, to równanie toru punktu będzie odcinkiem prostej o równaniu

lub odpowiednio

Kiedy zaś różnica faz j=± p/2 , to równanie (43) można zapisać jako

 

W tym przypadku, gdy w_x= w _y, układ poruszać się będzie po elipsie, która przejdzie w okrąg kiedy A_x = A_y. Dochodzimy do następującego stwierdzenia.

Jeżeli punkt materialny porusza się ruchem jednostajnym po okręgu w płaszczyźnie (x, y), to ruch jego rzutu na osie układu współrzędnych jest ruchem harmonicznym.

To interesujące stwierdzenie łączy ruch harmoniczny z ruchem jednostajnym po okręgu.

Ruch falowy jest to : ozchodzenie się w przestrzeni różnego rodzaju drgań, czyli zaburzeń stanu ośrodka. W zależności od ośrodków oraz charakteru zaburzeń rozróżnia się fale: mechaniczne (w tym sprężyste), elektromagnetyczne i f. materii (tzw. f. de Broglie'a).
FALE HANICZNE polegają na przekazywaniu od punktu do punktu zmian położenia, prędkości czy ciśnienia konkretnych obiektów materialnych (cząstek) i mogą się rozchodzić wyłącznie w ośrodkach materialnych. F.
ELEKTROMAGNETYCZNE wiążą się ze zmianą natężeń pól elektrycznych i magnetycznych istniejących również w próżni, a więc mogą rozchodzić się także poza ośrodkami materialnymi.
F. MATERII związane są ze zjawiskiem dualizmu falowo-korpuskularnego cząstek materii i mają istotnie odmienny charakter. Cechą ruchu falowego jest przenoszenie energii bez przenoszenia masy (substancji). Energia przenoszona przez f. maleje w miarę ich rozchodzenia się na skutek pochłaniania energii przez ośrodek i zamiany na inne rodzaje energii.

Fale sprężyste natomiast są to mechaniczne zaburzenia (odkształcenia) rozprzestrzeniające się w ośrodku sprężystym. Ciała zewnętrzne powodujące owe zaburzenia ośrodka nazywają się źródłami fal. Rozchodzenie się fal sprężystych polega na wzbudzaniu drgań cząstek ośrodka coraz bardziej odległych od źródła fal. Najważniejszą cechą odróżniającą fale sprężyste od dowolnego innego uporządkowanego ruchu cząstek ośrodka jest to, że w przypadku małych zaburzeń (przybliżenie liniowe) rozchodzenie się fal sprężystych nie jest związane z przenoszeniem substancji. Ze względu na kierunek drgań ośrodka rozróżniamy fale podłużne i poprzeczne.

Zasada Huygensa (czytaj: hojchensa) sformułowana przez Christiaana Huygensa mówiąca, iż każdy punkt ośrodka, do którego dotarło czoło fali można uważać za źródło nowej fali kulistej. Fale te zwane są falami cząstkowymi i interferują ze sobą. Wypadkową powierzchnię falową tworzy powierzchnia styczna do wszystkich powierzchni fal cząstkowych i ją właśnie obserwujemy w ośrodku.

Z zasady Huygensa wynika, iż fale rozchodzą się izotropowo, a więc również wstecznie. W rzeczywistości nie jest to osiągalne, co zostało udowodnione empirycznie. Poprawkę zasady wprowadził Kirchhoff dodając współczynnik kierunkowy, równy:

Interferencja to zjawisko nakładania się fal prowadzące do zwiększania lub zmniejszania amplitudy fali wypadkowej. Interferencja zachodzi dla wszystkich rodzajów fal, we wszystkich ośrodkach, w których mogą rozchodzić się dane fale. W ośrodkach nieliniowych oprócz interferencji zachodzą też inne zjawiska wywołane nakładaniem się fal, w ośrodkach liniowych fale ulegając interferencji spełniają zasadę superpozycji.

eżeli fala rozchodzi się w ośrodku rzadkim i odbije od gęstego, to zmienia fazę na przeciwną (do drogi optycznej dodaje się
). Jeśli natomiast rozchodzi się w gęstym i odbija od rzadkiego, to faza pozostaje bez zmian (nie zmienia się na przeciwną)

Dyfrakcja to zjawisko fizyczne zmiany kierunku rozchodzenia się fali na krawędziach przeszkód oraz w ich pobliżu. Zjawisko zachodzi dla wszystkich wielkości przeszkód, ale wyraźnie jest obserwowane dla przeszkód o rozmiarach porównywalnych z długością fali.

Dyfrakcja używana jest do badania fal, oraz obiektów o niewielkich rozmiarach, w tym i kryształów, ogranicza zdolność rozdzielczą układów optycznych.
Jeżeli wiązka fal przechodzi przez szczelinę lub omija obiekt, to zachodzi zjawisko ugięcia. Zgodnie z zasadą Huygensa fala rozchodzi się w ten sposób, że każdy punkt fali staje się nowym źródłem fali, tak powstałe fale rozchodzą się jako fale kuliste a fala w każdym punkcie jest sumą wszystkich fal (interferencja). Za przeszkodą pojawią się obszary wzmocnienia i osłabienia rozchodzących się fal.

Zjawisko dyfrakcji występuje dla wszystkich rodzajów fal np. fal elektromagnetycznych, fal dźwiękowych oraz fal materii.

Jeden z najprostszych przykładów zjawiska dyfrakcji zachodzi, gdy równoległa wiązka światła (np z lasera) przechodzi przez wąską pojedynczą szczelinę zwaną szczeliną dyfrakcyjną. Zgodnie z zasadą Huygensa każdy punkt szczeliny o szerokości d, jest nowym źródłem fali. Między źródłami zachodzi interferencja, co powoduje wzmacnianie i osłabianie światła rozchodzącego się w różnych kierunkach. Dla pojedynczej szczeliny jasność w funkcji kąta odchylenia od osi przyjmuje postać:

, dzie: - intensywność światła, ₀ - intensywność światła w maksimum czyli dla kąta równego 0, - długość fali, - szerokość szczeliny, unkcja sinc(x) = sin(x)/x.

Fala stojąca — fala, której pozycja w przestrzeni pozostaje niezmienna. Fala stojąca może zostać wytworzona w ośrodku poruszającym się względem obserwatora lub w przypadku interferencji dwóch fal poruszających się w przeciwnych kierunkach.

Fala stojąca to w istocie drgania ośrodka nazywane też drganiami normalnymi. Idealna fala stojąca nie jest więc falą - drgania się nie propagują. Miejsca gdzie amplituda fali osiąga maksima nazywane są strzałkami, zaś te, w których amplituda jest zawsze zerowa węzłami fali stojącej. Rysunek przedstawia idealną (zupełną) falę stojącą. W przypadkach rzeczywistych zwykle porusza się ona tam i z powrotem w ograniczonym obszarze przestrzeni (niezupełna fala stojąca).

Ciecz - stan skupienia materii - pośredni między ciałem stałym a gazem, w którym ciało fizyczne trudno zmienia objętość, a łatwo zmienia kształt. Wskutek tego ciecz przyjmuje kształt naczynia, w którym się znajduje, ale w przeciwieństwie do gazu nie rozszerza się, aby wypełnić je całe. Powierzchnia styku cieczy z gazem lub próżnią nazywa się powierzchnią swobodną cieczy.

Istnienie cieczy ogranicza od strony niskich temperatur temperatura krzepnięcia, a od wysokich temperatura wrzenia. Czysta ciecz może istnieć w temperaturze niższej od temperatury krzepnięcia - nazywana jest wówczas cieczą przechłodzoną. Może ona także istnieć w temperaturze wyższej od temperatury wrzenia - jest wtedy nazywana cieczą przegrzaną. Ciecz przechłodzona lub przegrzana jest w nietrwałym stanie termodynamicznym i pod wpływem zanieczyszczenia lub zaburzenia odpowiednio krzepnie lub wrze. Niektóre substancje ciekłe o dużej lepkości nie krystalizują się, pozostając w stanie amorficznym, które formalnie biorąc jest cieczą przechłodzoną.

Własności cieczy wynikają z zachowania się jej cząsteczek:

podobnie jak w gazie, mają one pełną swobodę przemieszczania się w objętości zajmowanej przez ciecz ystępują między nimi oddziaływania międzycząsteczkowe, które się jednak w obrębie objętości cieczy znoszą nawzajem. ddziaływania międzycząsteczkowe nie znoszą się na granicy cieczy z inną fazą na skutek czego występuje zjawisko zwane napięciem powierzchniowym.

Dyfuzja - proces rozprzestrzeniania się cząsteczek lub energii w danym ośrodku (np. w gazie, cieczy lub ciele stałym), będący konsekwencją chaotycznych zderzeń cząsteczek dyfundującej substancji między sobą i/lub z cząsteczkami otaczającego ją ośrodka. Podstawowym parametrem opisującym dyfuzję jest współczynnik dyfuzji. Dla tej samej substancji, w tych samych warunkach, współczynniki dyfuzji śledzonej i chemicznej są zwykle różne, gdyż drugi z tych współczynników uwzględnia oddziaływania i korelacje pomiędzy trajektoriami poszczególnych dyfundujących cząsteczek.

Napięcie powierzchniowe - zjawisko fizyczne występujące na styku powierzchni cieczy z ciałem stałym, gazowym lub inną cieczą. Polega na powstawaniu dodatkowych sił działających na powierzchnię cieczy w sposób kurczący ją (dla powierzchni wypukłej przyciągający do wnętrza cieczy, dla wklęsłej odwrotnie). Zjawisko to ma swoje źródło w siłach przyciągania pomiędzy molekułami cieczy. Występuje ono zawsze na granicy faz termodynamicznych, dlatego zwane jest też napięciem międzyfazowym .

Efektem napięcia powierzchniowego jest np. utrudnione zanurzanie w cieczy ciał nie podatnych na zwilżanie tą cieczą (znika ono w momencie całkowitego zanurzenia takiego ciała). Innym zjawiskiem związanym z napięciem powierzchniowym jest podnoszenie się (np. woda) lub opadanie (np. rtęć) cieczy w wąskich rurkach, tzw. kapilarach - zjawisko to należy do zjawisk kapilarnych.

Miarą napięcia powierzchniowego jest praca, jaką trzeba wykonać, by utworzyć jednostkową powierzchnię cieczy, co można wyrazić wzorem:

(jednostką w SI J/m²). dzie: (używa się też oznaczenia σ) - napięcie powierzchniowe, - praca potrzebna do utworzenia powierzchni A, - pole powierzchni.

Powyższy wzór jest równoważny:

(jednostką w SI N/m = J/m²). dzie: - siła napięcia powierzchniowego działająca równolegle do powierzchni cieczy, dążąca do zmniejszenia powierzchni cieczy, - długość odcinka na której działa siła. zór ten odpowiada definicji napięcia powierzchniowego: Napięciem powierzchniowym γ nazywa się siłę styczną do powierzchni cieczy, działającą na jednostkę długości obrzeża powierzchni cieczy.

W termodynamice napięcie międzyfazowe definiuje się wzór:

,

gdzie G to Entalpia swobodna zwana energią Gibbsa, a A wielkość powierzchni.

Zjawiska kapilarne Włoskowatość to cały szereg zjawisk związanych z zachowaniem par i cieczy a pojawiających się dla wielu obiektów o małym wymiarze charakterystycznym (np. rurki kapilarne) i silnie zależne od tego wymiaru, przy kącie zwilżania powyżej 90 stopni. W zależności od zwilżania i średnicy rurki zjawisko może się pojawiać lub zanikać - zachodzi ono do momentu, gdy ciężar słupa wody równoważy siły kapilarne.

Wzór na ciężar słupa wody:

- ciężar słupa wody _k - wysokość wzniosu kapilarnego - promień rurki - gęstość wody - przyciągania ziemskie

Wzór na siłę napięcia powierzchniowego

Q_p - siła napięcia powierzchniowego - promień rurki _p - napięcie powierzchniowe o przyrównaniu obu stron równania i podstawieniu danych dla wody i rurek ze szkła kwarcowego, otrzymujemy wysokość podciągania kapilarnego:

Równanie Bernoullego opisuje zachowanie gęstości energii całkowitej na linii prądu. Obowiązuje ono w podstawowej wersji dla płynu doskonałego, w wersji rozszerzonej dla płynu barotropowego. Wynika z zasady zachowania energii

Założenia: ciec jest nieściśliwa iecz nie jest lepkaprzepływ stacjonarny i bezwirowy

gdzie: _m - energia jednostki masy płynuρ - gęstość cieczyv - prędkość cieczy w rozpatrywanym miejscuh - wysokość w układzie odniesienia, w którym liczona jest energia potencjalna g- przyspieszenie grawitacyjne p- ciśnienie cieczy w rozpatrywanym miejscu

Poszczególne człony to: energia kinetyczna, energia potencjalna przyciągania ziemskiego, energia ciśnienia.

Równaniem Bernoullego opisuje wiele na co dzień obserwowanych zjawisk, zależności, a także zasad działania licznych urządzeń technicznych:

paradoks hydrodynamicznyzjawisko zrywania dachów, gdy wieje silny wiatrzasada działania sondy Pitotazasada działania Rurki Prandtlazasada działania zwężki Venturiegozasada działania palnika Bunsenapośrednio zasady powstawania siły nośnej w skrzydle samolotupośrednio w powstawaniu efektu Magnusa rzyczyna osiadania statków w ruchu na płytkim akwenie.

Równanie ciągłości strugi - jeżeli założymy, że dla płynu nieściśliwego temperatura jest stała i jednakowa dla każdego przekroju rurociągu to objętość płynu wpływającego i odpływającego w ciągu jednej sekundy z dowolnego przekroju przewodu jest stała.

V = F1xc1 = F2xc2 = F3xc3 = const

Ciecz nazywamy idealną, jeśli jest całkowicie nieściśliwa i pozbawiona lepkości. W rzeczywistości takiej cieczy nie ma.

Lepkość. Podczas przepływu cieczy rzeczywistych obserwuje się zjawisko tarcia wewnętrznego pomiędzy warstwami poruszającego się płynu. Tarcie to zwane lepkością pojawia się na skutek działania sił spójności pomiędzy cząsteczkami płynu. Skutkiem lepkości jest gradient prędkości warstw cieczy płynącej w przewodzie. Warstwa przylegająca do ścianek przewodu jest nieruchoma, a prędkość warstw rośnie w miarę zbliżania się do przodu. Taki warstwowy ruch cieczy nazywany jest laminarnym.

Równanie Newtona Zjawisko lepkości opisuje ilościowo prawo Newtona, które mówi, że aby zapewnić stałą różnicę prędkości Δv między warstwami o powierzchni S odległymi o Δx musi działać siła
Siła ta jest równa lecz przeciwnie skierowana do siły lepkości F= -F_L

Pole elektryczne - pole fizyczne, stan przestrzeni w której na ładunek elektryczny działa siła. Pole to opisuje się przez natężenie pola elektrycznego lub potencjał elektryczny.

Natężenie pola elektrycznego jest wektorową wielkością fizyczną opisującą pole elektryczne, równą stosunkowi wektora siły oddziaływania elektrostatycznego (F) działającej na umieszczony w danym punkcie pola ładunek próbny (Q) do wartości tego ładunku. Wzór na natężenie pola:

Ładunek próbny musi być na tyle mały by nie wpływał na rozkład ładunków w badanym obszarze. Zgodnie z definicją, jednostką natężenia pola elektrycznego niuton na culomb
co jest równoważne wolt na metr
.

Natężenie pola elektrycznego obrazuje się stosując techniki używane do obrazowania pól wektorowych, rysując linie pola (linie styczne do wektora pola), linie / powierzchnie ekwipotencjalne (prostopadłe do linii pola).

Prawo Coulomba głosi, że siła wzajemnego oddziaływania dwóch punktowych ładunków elektrycznych jest wprost proporcjonalna do iloczynu tych ładunków i odwrotnie proporcjonalna do kwadratu odległości między ich środkami. Jest to podstawowe prawo elektrostatyki. Prawo to można przedstawić za pomocą wzoru:

, w którym: F - siła wzajemnego oddziaływania dwóch punktowych ładunków elektrycznych, q₁ , q₂ - punktowe ładunki elektryczne, r - odległość między ładunkami, k - współczynnik proporcjonalności:

Z prawa tego wynika między innymi, że:

Im większy ładunek będą posiadały przedmioty, tym między nimi będzie większa siła; także im większa odległość będzie między przedmiotami, tym mniejsza siła będzie między nimi.

Strumień pola jest wielkością skalarną opisującą pole wektorowe oraz jego źródłowość. Definicja formalna strumienia pola opisywanego wektorem
przechodzącego przez daną powierzchnię S to:

Definicja ta jest zgodna z intuicyjnym pojęciem strumienia, np. jeżeli jako pole wektorowe weźmiemy iloczyn gęstości wody i jej prędkości w danym punkcie (pole prędkości) to strumień takiego pola będzie opisywał ilość(masę) wody przechodzącą przez zadaną powierzchnię w jednostce czasu, czyli to co intuicyjnie rozumiemy jako strumień. Szczególnie ważnym pojęciem jest strumień przechodzący przez powierzchnię zamkniętą:

Jeżeli wartość tego strumienia jest większa od zera oznacza to, że pole jest źródłowe i posiada wewnątrz tej powierzchni "źródło" (np. dla pola elektrycznego ładunek dodatni, dla analogii z wodą rurę wpływową), jeżeli wartość ta jest ujemna pole posiada "odpływ" (ładunek ujemny, rurę odpływową).

Praca prądu elektrycznego jest sumą prac sił opisujących oddziaływanie poruszających się ładunków elektrycznych z siecią krystaliczną przewodnika (grzałki, żarówki, itp.) lub z innymi poruszającymi się ładunkami wytwarzającymi pole magnetyczne (silniki prądu stałego).

Praca prądu elektrycznego w obwodzie prądu stałego jest równa iloczynowi napięcia źródła energii elektrycznej, natężenia prądu przepływającego przez odbiornik oraz czasu przepływu prądu. W przypadku zmian natężenia prądu lub napięcia praca jest sumą prac elementarnych podobnie jak w przypadku zmian siły.

Jednostką pracy w tym przypadku jest dżul (J) określany jako wolt·amper·sekunda

W skali makroskopowej, przy przepływie prądu elektrycznego przez rezystor, praca prądu zamieniana jest na ciepło. Przy przepływie prądu przez silnik elektryczny praca prądu zamieniana jest na pracę mechaniczną.

Energia potencjalna w polu elektrostatycznym Wyliczając energię potencjalną ładunku próbnego w danym punkcie pola skorzystamy z takiej własności, że różnica energii potencjalnych w dwóch punktach jest równa pracy wykonanej przy przemieszczaniu tego ładunku próbnego z jednego punktu do drugiego (tak samo robiliśmy wliczając energię potencjalną w polu grawitacyjnym). Aby wyliczyć energię potencjalną w danym punkcie należy przemieścić ten ładunek próbny do tego punktu z miejsca gdzie energia potencjalna równa jest zero. Takie miejsce jest w punkcie nieskończenie oddalonym od źródła. Zatem:

Znak dodatni, czy ujemny energii potencjalnej wybieramy w zależności czy ładunek ze źródłem się odpychają, czy przyciągają.

Kondensator to element elektryczny (elektroniczny) zbudowany z dwóch przewodników (okładzin) rozdzielonych dielektrykiem. Doprowadzenie napięcia do okładzin kondensatora powoduje zgromadzenie się na nich ładunku elektrycznego. Jeżeli kondensator jako całość nie jest naelektryzowany, to cały ładunek zgromadzony na jego okładkach jest jednakowy, ale przeciwnego znaku. Kondensator charakteryzuje pojemność określająca zdolność kondensatora do gromadzenia ładunku:

gdzie: C - pojemność, w faradach Q - ładunek zgromadzony na jednej okładce, w kulombach U - napięcie elektryczne między okładkami, w woltach.

Pojemność wyrażana jest w faradach. Jeden farad to bardzo duża jednostka, dlatego w praktyce spotyka się kondensatory o pojemnościach piko-, nano-, mikro- i milifaradów.

Pojemnością elektryczną kondensatora nazywamy stosunek ładunku zgromadzonego na jego okładce do różnicy potencjałów między okładkami:

C = Q/ΔV

Prawo Gaussa dla elektryczności w fizyce zwane również twierdzeniem Gaussa to prawo wiążące pole elektryczne z jego źródłem czyli ładunkiem elektrycznym.

Pole elektryczne jest polem wektorowym, dlatego też zgodnie z twierdzeniem Gaussa-Ostrogradskiego można zdefiniować wielkość zwaną strumieniem natężenia pola: strumień natężenia pola elektrycznego przenikający przez dowolną powierzchnię zamkniętą w jednorodnym środowisku o bezwzględnej przenikalności dielektrycznej ε, jest równy stosunkowi całkowitego ładunku znajdującego się wewnątrz tej powierzchni do wartości tejże przenikalności.

Prąd stały - w odróżnieniu od prądu zmiennego i przemiennego prąd stały charakteryzuje się stałą wartością natężenia oraz kierunkiem przepływu.

Dla urządzeń, które używane są w pobliżu sieciowej energii elektrycznej stosuje się zasilanie prądem stałym wytwarzanym przez zasilacze sieciowe. W zasilaczu sieciowe napięcie przemienne jest najpierw transformowane na odpowiedni poziom napięcia, prostowane za pomocą mostka Graetza oraz filtrowane, tak aby jego ostateczny przebieg był jak najbardziej zbliżony do wartości stałej.

Moc dowolnego odbiornika w układzie prądu stałego jest obliczana jako:

gdzie: P - moc, U - stałe napięcie elektryczne, I - stały prąd elektryczny.

Natężeniem prądu i nazywamy stosunek ładunku Δq przepływającego przez przekrój poprzeczny przewodnika do czasu &#t, w kórym ładunek ten przepływa:

i = Δq/Δt Jeżeli wartość natężenia prądu i jego zwrot nie zmieniają się w czasie, to nazywa się on prądem stałym. Natężenie prądu można wtedy zapisać jako: i=q/t

Jednostką natężenie jest amper (A). Jest to natężenie prądu stałego, przy którym w czasie 1s przepływa łądunek 1 C. Ta definicja ampera nie służy do pomiaru wzorca jednostki natężenia, ponieważ występują trudności praktyczne z precyzyjnym pomiarem ładunku przepływającym w określonym czasie przez przewodnik. Dlatego w układzie SI amper jest zdefiniowany za pomocą sił oddziaływania magnetycznego przewodników z prądem. Tę definicję można znaleść w dziele magnetyzm

Napięcie elektryczne - różnica potencjałów elektrycznych między dwoma punktami obwodu elektrycznego lub pola elektrycznego. Napięcie elektryczne to stosunek pracy wykonanej podczas przenoszenia ładunku między punktami, dla których określa się napięcie do wartości tego ładunku.

Przy założeniu, że przenoszony ładunek jest na tyle mały, że nie wpływa na otoczenie. W przypadku źródła napięcia (prądu) elektrycznego jest jego najważniejszym parametrem i określa zdolności źródła energii elektrycznej do wykonania pracy. Napięcie na źródle napięcia jest mniejsze od siły elektromotorycznej źródła o spadek napięcia na oporze istniejącym wewnątrz źródła (opór wewnętrzny). Jednostką napięcia jest wolt (V), a symbolem napięcia we wzorach fizycznych jest U.

Siła elektromotoryczna (SEM) - czynnik powodujący przepływ prądu w obwodzie elektrycznym ^[1] równy energii elektrycznej uzyskanej przez jednostkowy ładunek przemieszczany w urządzeniu (źródle) prądu elektrycznego w przeciwnym kierunku do sił pola elektrycznego oddziałującego na ten ładunek. Źródło siły elektromotorycznej przenosi ładunek elektryczny wbrew siłom pola elektrycznego. Siły przenoszące ładunek są nazywane siłami postronnymi. Siły postronne przenosząc ładunek wykonują pracę nad ładunkiem. Siła elektromotoryczna źródła jest zdefiniowana jako iloraz pracy wykonanej przez źródło do wartości przenoszonego ładunku. ^[4]

gdzie:
- siła elektromotoryczna, W - praca, q - przepływajacy ładunek. Jednostką siły elektromotorycznej jest dżul na kulomb równy voltowi.

Prawo Ohma mówi, że natężenie prądu stałego I jest proporcjonalne do całkowitej siły elektromotorycznej w obwodzie zamkniętym lub do różnicy potencjałów (napięcia elektrycznego) między końcami części obwodu nie zawierającej źródeł siły elektromotorycznej. Prawidłowość tę odkrył w 1827 roku niemiecki fizyk, profesor politechniki w Norymberdze i uniwersytetu w Monachium Georg Simon Ohm. Można ją opisać jako:

Współczynnik proporcjonalności w tej relacji nazywany jest konduktancją, oznaczaną przez G.

lub w ujęciu tradycyjnym:

Odwrotność konduktancji nazywa się oporem elektrycznym przewodnika:

Prawo Ohma określa opór elektryczny przewodnika:

Prawo to jest prawem doświadczalnym i jest dość dokładnie spełnione dla ustalonych warunków przepływu prądu, szczególnie temperatury przewodnika. Materiały, które się do niego stosują, nazywamy przewodnikami omowymi lub "przewodnikami liniowymi" - w odróżnieniu od przewodników nieliniowych, w których opór jest funkcją natężenia płynącego przez nie prądu. Prawo to także nie jest spełnione gdy zmieniają się parametry przewodnika, szczególnie temperatura. Ze wszystkich materiałów przewodzących prawo Ohma najdokładniej jest spełnione w przypadku metali.

Prawa Kirchhoffa - dwa prawa dotyczące obliczania natężeń i napięć stałego prądu elektrycznego w obwodach elektrycznych, sformułowane przez niemieckiego fizyka Gustava Kirchhoffa,

Pierwsze prawo Kirchhoffa: Suma algebraiczna natężeń prądów dopływających(+) i odpływających(-) z danego węzła jest równa 0. lub Suma natężeń prądów dopływających do węzła jest równa sumie natężeń prądów wypływających z tego węzła. W zależności od użytego aparatu matematycznego prawo to jest w różny sposób przedstawiane w postaci wzorów.

Dla każdego węzła obwodu elektrycznego suma algebraiczna wartości chwilowych prądów jest równa zeru.

Przyjmuje się konwencję, że prądy zwrócone do węzła mają znak (+), zaś prądy ze zwrotem od węzła mają znak (-), np.:

Drugie prawo Kirchhoffa - zwane również Prawem napięciowym, dotyczy bilansu napięć w zamkniętym obwodzie elektrycznym.

Treść prawa: Suma wartości chwilowych sił elektromotorycznych występujących w obwodzie zamkniętym równa jest sumie wartości chwilowych napięć elektrycznych na elementach pasywnych tego obwodu:

Gdzie
to wartość chwilowa sem k-tego źródł;
- napięcie na l-tym elemencie oczka. Prawo to występuje również w prostszej wersji:

Suma napięć źródłowych w dowolnym obwodzie zamkniętym prądu stałego równa jest sumie napięć na odbiornikach.

Drugie Prawo Kirchhoffa nie jest słuszne, gdy przez obwód zamknięty przepływa zmienny w czasie strumień magnetyczny

Pole magnetyczne jest stanem (własnością) przestrzeni, w której siły działają na poruszające się ładunki elektryczne, a także na ciała mające moment magnetyczny niezależnie od ich ruchu. Pole magnetyczne jest obok pola elektrycznego przejawem pola elektromagnetycznego. W zależności od opisu (obserwatora), to samo zjawisko może być opisywane jako objaw pola elektrycznego, magnetycznego lub obu.

Pole magnetyczne jest polem wektorowym, wielkości fizyczne używane do opisu pola magnetycznego to indukcja magnetyczna B oraz natężenie pola magnetycznego H (te dwie wielkości są powiązane ze sobą poprzez przenikalność magnetyczną).

Obrazowo pole magnetyczne przedstawia się jako linie pola magnetycznego. Kierunek pola określa ustawienie igły magnetycznej lub obwodu, w którym płynie prąd elektryczny.

Indukcja magnetyczna w fizyce wielkość wektorowa opisująca pole magnetyczne. Wektor ten określa siłę Lorentza, z jaką pole magnetyczne działa na poruszający się w nim ładunek elektryczny :

gdzie
jest siłą działającą na ładunek q, poruszający się z prędkością
w polu o indukcji magnetycznej
.

Jednostką indukcji magnetycznej jest jedna Tesla 1T

Skalarnie wzór ten można zapisać:

gdzie α - kąt pomiędzy wektorem prędkości a wektorem indukcji.

Wartość indukcji magnetycznej jest równa sile działającej na ładunek 1 Coulomba poruszający się w polu magnetycznym z prędkością 1 metra na sekundę, prostopadle do jego linii sił:

Powyższy wzór można przekształcić do postaci:

Wtedy wartość indukcji magnetycznej wyrażać się będzie przez siłę działającą na przewodnik, przez który płynie prąd I, na którego na długości s działa jednorodne pole magnetyczne.

Prawo Biota-Savarta Wzór Biota - Savarta umożliwia obliczenie indukcji magnetycznej gdy znane jest natężenie prądu, który jest źródłem pola magnetycznego (punkty tego pola są scharakteryzowane przez wektor indukcji, a wartość tego wektora określa wzór Biota - Savarta). Wszystkie przyczynki do wektora indukcji pochodzące od elementów przewodnika mają w danym punkcie taki sam kierunek, który jest prostopadły do płaszczyzny w której leży przewodnik i analizowany punkt. Dlatego pole magnetyczne ma kształt okręgów leżących w płaszczyźnie prostopadłej do przewodnika, środkami których jest przewodnik, a indukcję magnetyczna określa wzór:

gdzie: I - natężenie prądu r - odległość od przewodnika.

Indukcja elektromagnetyczna - zjawisko powstawania siły elektromotorycznej w przewodniku pod wpływem zmiennego pola magnetycznego lub ruchu przewodnika w polu magnetycznym, odkryte w 1831 roku przez angielskiego fizyka Michaela Faradaya. Zjawisko indukcji opisuje prawo indukcji elektromagnetycznej Faradaya:

, gdzie:
to indukowana siła elektromotoryczna w woltach

Φ_B to strumień indukcji magnetycznej przebiegający przez powierzchnię objętą przewodnikiem,

Prawo indukcji elektromagnetycznej Faradaya to prawo oparte na doświadczeniach Faradaya z 1831 roku. Wyraża relację pomiędzy zmianą wartości strumienia magnetycznego przechodzącego przez obszar objęty przez zamkniętą pętlę i pola elektrycznego wyindukowanego na tej pętli:

Może też być wyrażone w postaci:

gdzie: V - siła elektromotoryczna powstająca w pętli, E - natężene wyindukowanego pola elektrycznego, l - pętla, dl - nieskończenie mały odcinek pętli, Φ_B - strumień indukcji magnetycznej, dt - nieskończenie mały odcinek czasu, s - powierzchnia zamknięta pętlą l, B - indukcja magnetyczna.

PRĄD PRZEMIENNY Nazywamy taki prąd, którego wartość natężenia i kierunek przepływu zmieniają się okresowo. Najczęściej spotykanym prądem przemiennym jest prąd sinusoidalny.
NATĘŻENIE SKUTECZNE Nazywamy natężenie prądu stałego, którego moc jest równa mocy rozważanego prądu przemiennego ( prąd stały w danej jednostce czasu wykona taką samą pracę jaką wykonałby prąd przemienny
NAPIĘCIE SKUTECZNE Nazywamy napięcie prądu stałego, którego moc jest równa mocy rozważanego prądu przemiennego
MOC PRĄDU PRZEMIENNEGO Jest równa iloczynowi napięcia skutecznego, natężenia skutecznego i cosinusa kąta alfa przesunięcia fazowego

Ciepło w termodynamice to jedna z form, obok pracy, przekazywania energii termicznej. Jest funkcją procesu.

Ciepło przepływa między ciałami, które znajdują się w stosunku do siebie w nierównowadze termicznej, tzn. gdy posiadają one różne temperatury. W niektórych, szczególnych przypadkach może ono jednak także przepływać między ciałami, których temperatury są jednakowe.

Ciepło właściwe - energia termiczna potrzebna do podniesienia temperatury jednej jednostki masy ciała o jedną jednostkę temperatury. W układzie SI ciepło właściwe podaje się w dżulach na kilogram razy kelwin (J/(kg*K)). Ciepło właściwe jest to wielkość, która charakteryzuje każdą substancję pod względem energetycznym. Ciepło właściwe (oznaczane małą literą c) wprowadza się jako współczynnik proporcjonalności w prawie fizycznym mówiącym, że:

Zmiana energii wewnętrznej (ΔE) ciała jest proporcjonalna do masy ciała (m) i zmiany temperatury (Δt).

Prawo to jest prawem doświadczalnym i spełnione jest z pewnym przybliżeniem oraz pod warunkiem, że ciało nie zmienia stanu skupienia lub fazy.

Formalnie ciepło właściwe określa wzór:

gdzie: c - ciepło właściwe, (J/kg K), m - masa substancji, Q - ciepło dostarczane do układu, T - temperatura.

Ciepło właściwe ciał stałych i cieczy jest niezmienną cechą zależną tylko od struktury chemicznej tych ciał i nie zależy od ich kształtu i rozmiarów. Ciepło właściwe większości substancji zmienia się jednak nieznacznie ze zmianami temperatury nawet w obrębie jednego stanu skupienia.

Ciepło topnienia jest to ilość energii potrzebnej do stopienia jednostki masy danej substancji. W układzie SI jednostką ciepła topnienia jest J/kg (dżul na kilogram).

gdzie: Q-Ilość energii m-masa ciała q-ciepło topnienia

Bilans cieplny - w termodynamice to równanie opisujące sumę procesów cieplnych określonego układu termodynamicznego. W pewnym sensie kompletny zapis bilansu cieplnego jest równoważny sformułowaniu I zasady termodynamiki dla szczególnego przypadku analizowanego układu. Bilans cieplny uwzględnia: sumę ciepła dostarczanego do układu z otoczenia sumę ciepła, którą układ wydziela na zewnątrz efekt cieplny procesów zachodzących wewnątrz układu Zgodnie z I zasadą termodynamiki, różnica wartości energii termicznej dostarczanego i wydzielanego przez układ musi równać się zmianie energii wewnętrznej układu. Gdy w układzie nie zachodzą procesy zmieniające jego energię wewnętrzną, lub suma tych procesów jest równa 0, ciepło dostarczane do układu musi być równe ciepłu wydzielanemu. Prowadzi to do dość oczywistego wniosku, który jest niczym innym jak sformułowaniem I zasady termodynamiki, że w układzie zamkniętym, suma procesów cieplnych jaka w nim zachodzi nie może zmienić jego ogólnej energii wewnętrznej. Każdy bilans ciepła można zapisać z "punktu widzenia" układu lub otoczenia.

Przewodność cieplna, inaczej współczynnik przewodnictwa ciepła, określa zdolność substancji do przewodzenia ciepła. W tych samych warunkach więcej ciepła przepłynie przez substancję o większym współczynniku przewodności cieplnej.

Definicja: Dla ciała o kształcie prostopadłościanu (pręta) przewodzącego ciepło w warunkach w warunkach stanu stabilnego ilość przekazanego ciepła jest zależna od substancji, proporcjonalna do przekroju ciała, różnicy temperatur oraz czasu przepływu ciepła:

Z powyższego wynika:

Gdzie: k - współczynnik przewodnictwa cieplnego, ΔQ - ilość ciepła przepływającego przez ciało, Δt - czas przepływu, L - długości (ciała) pręta, S - przekrój poprzeczny pręta, ΔT - różnica temperatur w kierunku przewodzenia ciepła.

Jednostką współczynnika przewodzenia ciepła w układzie SI - J/(m s K) = W m^-1 K^-1 (wat na metr kelwin).

Konwekcja - proces przenoszenia ciepła wynikający z ruchu materii w objętości dowolnej substancji, np. powietrza, wody, piasku itp. Czasami przez konwekcję rozumie się również sam ruch materii związany z różnicami temperatur, który prowadzi do przenoszenia ciepła. Ruch ten precyzyjniej nazywa się prądem konwekcyjnym.

Promieniowanie - strumień cząstek lub fal wysyłanych przez ciało.

Wytwarzanie promieniowania jest nazywane emisją.

Pierwotnie pojęcie promieniowanie używano do tych rodzajów wysyłanych cząsteczek i fal (bez wnikania w ich naturę), którego wąski strumień (promień patrz światło) rozchodząc się w przestrzeni może być traktowany jak linia w geometrii (nie rozdziela się).

Prawo Fouriera mówi, że gęstość przewodzonego strumienia ciepła jest wprost proporcjonalna do gradientu temperatury , [Wymiana ciepła, S. Wiśniewski, T.S. Wiśniewski, WNT'88]

Prawo Stefana-Boltzmanna opisuje całkowitą moc wypromieniowywaną przez ciało doskonale czarne w danej temperaturze:

gdzie Φ - strumień energii wypromieniowywany w kierunku prostopadłym do powierzchni ciała [W / m²] σ - stała Stefana-Boltzmanna T - temperatura w skali Kelvina

Prawo Wiena - prawo opisujące promieniowanie elektromagnetyczne emitowane przez ciało doskonale czarne. Ze wzrostem temperatury widmo promieniowania ciała doskonale czarnego przesuwa się w stronę fal krótszych, zgodnie ze wzorem:

gdzie:
- długość fali o maksymalnej mocy promieniowania mierzona w metrach

T- temperatura ciała doskonale czarnego mierzona w kelwinach,

- stała Wiena Prawo Wiena jest wnioskiem z rozkładu Plancka promieniowania ciała doskonale czarnego. Prawo Wiena zostało nazwane na cześć odkrywcy Wilhelma Wiena, który sformułował je na podstawie danych doświadczalnych w 1893 roku. Prawo Plancka zostało sformułowane w 1900 roku. Znajduje ono zastosowanie przy badaniu temperatur gwiazd, przy przyliżeniu, że promieniują one jak ciało doskonale czarne (co jest bliskie prawdy).

---