Metoda równań Kirfhhoffa: g- liczba gałęzi, n- liczba węzłów, n-1 równań z prawa prądowego kirchhoffa, g-(n-1) równań z prawa nap. Kirch. Dla dowolnych oczek niezależnych. Stosuje się ją do obwodów o małej il. Elementów, ze względu na to, że jest g równań i g niewiadomych i przy dużych obwodach jest złożone obliczeniowo.

Twierdzenie Thevenina: Dowolny obwód liniowy można zastąpić od strony zacisków AB uproszczonym obwodem równoważnym składającym się z szeregowego połączonych :idealnego źródła napięcia i impedancji zastępczej obwodu. Wartość źródła napięcia to napięcie na zaciskach AB po odłączeniu gałęzi, a impedancja jest widziana z zacisków AB, po wyłączeniu gałęzi AB i zwarci wszystkich źródeł napięcia i rozwarciu źródeł prądowych. Stosuje się, gdy mamy policzyć prąd w 1 wybranej gałęzi.

Twierdzenie Notona: Dowolny aktywny obwód liniowy można zastąpić obwodem złożonym z idealnego źródła prądowego i impedancji widzianej z zacisków AB. Wartość źródła prądowego to prąd zwarciowy gałęzi AB, a impedancja jest widziana z zacisków AB, po wyłączeniu gałęzi AB i zwarci wszystkich źródeł napięcia i rozwarciu źródeł prądowych. Stosuje się, gdy mamy policzyć prąd w 1 wybranej gałęzi.

Metoda potencjałów węzłowych: Liczba równań w tej metodzie jest równa liczbie węzłów niezależnych. Jeden wybrany przez nas węzeł odniesienia uziemiamy (jego pot.=0), a dla reszty zapisujemy równanie węzłowe. Stos. Gdy met. Kirchhoffa jest dużo równań.

Metoda prądów oczkowych: Jako zmienne wprowadza się prądy przypisane oczkom niezależnym.

Zasada superpozycji: Stosujemy ją, gdy w obwodzie jest wiele źródeł o różnych częstotliw. „Odpowiedź czasowa obwodu elektrycznego liniowego przy warunkach początkowych zerowych jest równa sumie odpowiedzi czasowych na każde wymuszenie z osobna.” Rzeczywiste źródła napięcia zwieramy, a przy rzeczywistych źródłach prądu robimy przerwę.

Sprzężenia: Jeśli 2 cewki znajdują się odpowiednio blisko siebie ich strumienie magn. przenikają się. Dla cewek sprzężonych magnetycznie definiuje się współczynnik sprzężenia: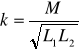
Przy idealnym sprzężeniu cewek k=1, przy braku sprężenia k=0. Sprzężenie powoduje indukowanie się w cewce napięcia w wyniku zmian prądu płynącego przez tą Ewkę oraz przez cewkę sprzężoną.
, Sprzężenie dodatnie i ujemne (rysunki).

Przy istnieniu sprzężenia magn. w cewce generowane jest napięcie nawet przy prądzie własnym =0. oznacza to, że przenoszona jest energia z jednego obwodu do 2 drogą magnetyczną.

Rezonans: Rezonansem nazywamy zgodność w fazie prądu i napięcia. Oznacza to, że argument urojony admitancji lub impedancji =0. Obwód nie pobiera mocy biernej (nastepuje jej kompensacja). Rezonans w którym występują RLC połączone szeregowo (głównie chodzi o L i C, bo to one są źródłem rezonansu) to rezonans szeregowy, w którym są połączone równolegle - jest równoległy.

Rezonans szeregowy: Załóżmy, że w obwodzie elementy RLC są połączone szeregowo i przyłożone jest do nich napięcie o pulsacji ω=2πf , rysunek i wyprowadzenie omegi rezonansowej oraz f - rezonansowej.

Parametry rezonansu: *częstotliwość rezonansowa, *dobroć Q stosunek napięcia skutecznego na el. reaktancyjnym (kondensator lub cewka) do nap. Skutecznego na el. rezystancyjnym, *impedancja w stanie rezonansu Zr=Re{Z}=R, *pasmo przenoszenia:<w1;w2>, dla którego p>=1/2 Pmax

Rezonans równoległy: Występuje przy równoległym połączeniu elementów RLC (a właściwie L i C), wtedy gdy urojona część admitancji =0.

Układy trójfazowe:

Metoda składowych symetrycznych (metoda obliczania awarii) - polega ona na tym, że stosując odpowiednie przekształcenia liniowe zastępuje się układ trzech wektorów niesymetrycznych przez równoważne 3 wektory symetryczne.

Takiemu układowi można przyporządkować równoważny układ 3 źródeł trójfazowych, reprezentujące:

- składową zerową (brak przesunięcia między napięciami fazowymi)

- składową zgodną (B opóźnia się wzgl. A, C wyprzedza A)

- składową przeciwną (B wyprzedza A, C opóźnia się wzgl. A)

---