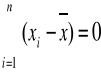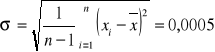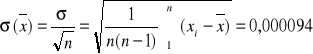Ćw. 6 (AiR): OCENA BŁĘDÓW PRZYPADKOWYCH

Celem ćwiczenia jest poznanie podstawowych pojęć z zakresu statystyki i rachunku prawdopodobieństwa, stosowanych w ocenie dokładności pomiarów z błędami przypadkowymi. Ćwiczenie przedstawia sposób postępowania dla dużej serii pojedynczych odczytów, tj. o liczności większej od 30.

1. BŁĘDY SYSTEMATYCZNE I PRZYPADKOWE

Podstawowy podział błędów wyróżnia błędy systematyczne i przypadkowe. Kryterium tej klasyfikacji zakłada ich odmienny wpływ na wyniki kolejnych pomiarów tej samej wielkości, a wykonanych w niezmiennych warunkach. Jeżeli uzyskane wtedy wyniki są jednakowe, to pomiary obarczone są stałym błędem systematycznym.¹ Gdy natomiast kolejne wyniki zmieniają się w sposób nieprzewidywalny (przypadkowy), to w takich pomiarach występują błędy przypadkowe.

Jest charakterystyczne, że dla błędów systematycznych możemy określić źródła ich pochodzenia i wyznaczyć ich wartości - dzięki temu uzyskujemy możliwość ograniczenie ich wpływu na wynik pomiaru, co prowadzi do polepszenia dokładność pomiaru. Wykonuje się to na wiele sposobów, np. obliczając błąd metody i wprowadzając go do wyniku pomiaru w postaci poprawki, można też wykonać pomiar dokładniejszą metoda pomiarową lub wykorzystać do pomiaru dokładniejszy przyrząd pomiarowy.

Dla błędów przypadkowych ściśle nie znamy źródeł ich powstawania, ani ich wartości. Jedynie można je ograniczyć przez wytworzenie na tyle niezmiennych warunków pomiarów, aby uzyskany rozrzut (rozproszenie) wyników serii był jak najmniejszy.

Do określenia wpływu błędów przypadkowych na dokładność pomiarów stosuje się metody wykorzystywane w opisie zjawisk przypadkowych, a wynikające ze statystyki matematycznej i rachunku prawdopodobieństwa.

Błędy przypadkowe wywołują rozrzut wyników serii pomiarów o charakterystycznych właściwościach. Jeżeli seria odczytów ma znaczną liczność powtórzeń, to można zauważyć:

• występowanie środka rozproszenia wartości, teoretycznie przyjmowany za wartość rzeczywistą (prawdziwą) wielkości mierzonej;

• podobną liczbę pomiarów z wartościami mniejszymi i większymi względem wartości środka rozproszenia, oraz zachodzącą między nimi symetrię;

• dużo większą częstość występowania wyników z wartościami niewiele różniącymi się od wartości środka rozproszenia niż wyników o większej różnicy; wyników różniących się znacznie praktycznie nie ma;

2. POJĘCIA STATYSTYKI i OCENA BŁĘDÓW PRZYPADKOWYCH

Zdarzenie losowe - pojęcie nie definiowane ściśle; służy do opisu zjawisk przypadkowych, czyli takich, w których zajście konkretnego zdarzenia leży całkowicie lub częściowo poza zasięgiem kontroli ludzkiej. Zdarzenie losowe ma właściwość występowania lub nie występowania. Rachunek prawdopodobieństwa i statystyka matematyczna, badając modele matematyczne zjawisk przypadkowych, przypisuje zdarzeniu losowemu prawdopodobieństwo, tj. liczbę wyrażającą możliwość jego zajścia.

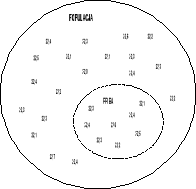
Populacja - są to wszystkie elementy zbioru (zdarzenia losowe); np. zbiór wartości rezystancji serii oporników o  jednakowych wartościach nominalnych (populacją skończona), zbiór wartości napięcia sieci (teoretycznie - populacja nieskończona).

Rys.1. Populacja i próba

Próba - wybrane do badań elementy populacji; od liczności i wyboru próby zależy jej reprezentatywność dla całej populacji.

Zmienna losowa - jeżeli każdemu ze zdarzeń losowych (populacji bądź próby) przyporządkuje się pewną liczbę rzeczywistą x, to zbiór tych liczb stanowi funkcję rzeczywistą zwaną zmienną losową. Zmienna losowa może być funkcją ciągłą lub dyskretną.

Histogram - wykres słupkowy obrazujący częstość występowania wartości zmiennej losowej w badanej próbie. Na podstawie empirycznie uzyskanego histogramu wnioskuje się o rozkładzie zmiennej losowej badanej próby.

Rozkład zmiennej losowej - obrazuje współzależność między wartościami x zmiennej losowej a prawdopodobieństwami ich wystąpienia p(x).

W przyrodzie i technice szczególne znaczenie odgrywa rozkład normalny. Służy do opisu takich zjawisk przypadkowych, w których występuje znaczna liczba zdarzeń losowych, na które wpływa w znikomym stopniu wiele niezależnie działających czynników. Przyjmuje się, że takie warunki występują też w pomiarach, czyli wielokrotne pomiary tej samej wielkości realizowane w niezmiennych warunkach daje przypadkowy rozrzut wyników o rozkładzie normalnym. Rozkład normalny opisany jest funkcją gęstości prawdopodobieństwa o postaci

.

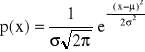
Parametrami rozkładu są: μ - wartość oczekiwana (wartość prawdziwa), σ - odchylenie standardowe losowej x (też nazywane odchyleniem średniokwadratowym) zmiennej.

Obraz funkcji gęstości prawdopodobieństwa rozkładu normalnego przedstawia rys. 2.

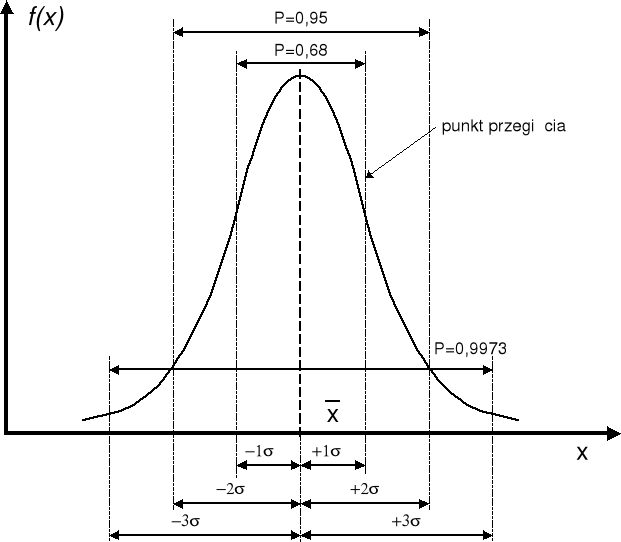
Rys. 2. Rozkład normalny

Z rozkładu normalnego wynika, że w przedziale ±σ znajduje się 68% wyników, a w przedziale ±2σ znajduje się 95% wyników, a w przedziale ±3σ znajduje się 99,73% wyników, czyli praktycznie wszystkie.

Ze względu na bardzo duże prawdopodobieństwo (graniczące z pewnością) wystąpienia pojedynczego wyniku pomiaru w przedziale ±3σ, to przedział ten wyznacz tzw. graniczną niepewność pojedynczego pomiaru, a zapis jego wyniku należy przedstawić następująco:

X = x_i ± 3σ , p=0,9973

gdzie p nazywane jest poziomem ufności.

Odchylenie standardowe obliczamy z zależności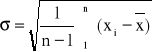
,

w której:
- średnia arytmetyczna z serii n pomiarów.

Dowodzi się, że w n pomiarach tej samej wielkości, wykonanych z jednakową starannością i tym samym przyrządem pomiarowym, przy spełnieniu też warunku pomijalnie małych błędów systematycznych, najbardziej prawdziwą (wiarygodną) wartością jest wartość średnia

, gdzie x_i jest wynikiem pojedynczego pomiaru.

Wartość średnia jest też zmienną losową o rozkładzie normalnym, dla której odchylenie standardowe jest
razy mniejsze niż odchylenie standardowe pojedynczego wyniku, czyli

.

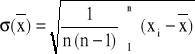
W związku z tym zapis wyniku pomiaru, przedstawiony wartością średnią i jej niepewnością pomiaru:
, należy przedstawić w jednej z poniższych postaci:

gdzie p - poziom ufności (prawdopodobieństwo wystąpienia wartości średniej w podanym przedziale niepewności).

Przedział niepewności
określa niepewność graniczną wartości średniej, podobnie jak dla przypadku niepewności pojedynczego wyniku serii.

Surowe wyniki pomiarów są obarczone tak błędami systematycznymi i jak też przypadkowymi. Zwykle w pomiarach o przeciętnych dokładnościach błędy przypadkowe są pomijalnie małe, a dla nie wyeliminowanych błędów systematycznych szacuje się ich granicę i uwzględnia się w ocenie dokładności pomiarów.

Błędy przypadkowe ujawniają się zwłaszcza w pomiarach dokładnych, w których są stosowane przyrządy pomiarowe o dużej dokładności i dużej rozdzielczości. Tutaj często eliminuje się błędy systematyczne, a wpływ błędów przypadkowych na wynik pomiaru szacuje się na podstawie serii pomiarów, oczywiście zapewniając w czasie ich trwania niezmienność warunków pomiarowych.

Jeżeli jednak w pomiarach dokładnych wystąpią też błędy systematyczne, których nie można wyeliminować, a mające wartości porównywalne z błędami przypadkowymi, to należy oszacować ich łączny wpływ na wynik pomiaru. Można np. sumować ich graniczne wartości, co przedstawia zamieszczony dalej przykład. W takich pomiarach należy postępować bardzo rozważnie, gdyż może się zdarzyć, że błędy systematyczne mogą zmienić rozkład błędów przypadkowych, a stąd dać wynik pomiarów mało wiarygodny.

3. PROGRAM ĆWICZENIA

1. Wykonać serię pomiarów wielkości wskazanej przez prowadzącego o liczności próby większej od 30. Z wyników serii odczytów obliczyć:

1. wartość średnią,

2. odchylenie standardowe,

3. odchylenie standardowe średniej,

4. dopuszczalny błąd graniczy przyrządu pomiarowego,

5. błąd graniczny pomiaru (względny i bezwzględny)

6. poprawnie opracować wynik pomiaru.

Tab.2.Wyniki pomiarów i obliczeń dla serii odczytów ....................................

i	xi
1
....
n
Wartość średnia
Odchylenie standardowe
Odchylenie standardowe średniej

2. Wykonać wykres x_i = f(i). Na wykresie przedstawić liniami wartości:
   ;
   ;
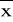
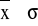
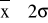
   oraz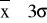
   . Oblicz liczbę wyników pomiarów w poszczególnych przedziałach: ±σ, ±2σ, ±3σ. Oblicz ich wartość względną (względem liczby wszystkich pomiarów) i porównaj z wartościami dla rozkładu normalnego: 0,65 ; 0,95 ; 0,997.

3. Sporządzić histogram - czyli wykres słupkowy częstości występowania x_i. W tym celu należy podzielić zakres zmierzonych wartości na nieparzystą liczbę równych podzakresy (7 lub 9), a następnie określić liczbę wartości występujących w poszczególnych podzakresach. Na wykresie przedstawić liniami wartości: średnią
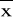
   oraz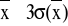
   .

4. Ocenić uzyskany histogram pod względem jego podobieństwa do rozkładu normalnego; sprawdzić też, czy wartość średnia należy do przedziału charakteryzującego się największą częstością występowania pomiaru.

4. PRZYKŁAD RACHUNKOWY

Przykładową ocenę rozrzutu serii odczytów wraz z opracowaniem wyniku pomiaru zamieszczono poniżej.

Tab. Wyniki pomiarów napięcia sieciowego 3.02.2005, godz. 15:10-15:15

data	3.02.2005		godz.15:10-15:15
typ przyrządu	HP 34402	numer fabryczny	US46017958
Niedokładność woltomierza	0,02%Ux+0,005%UZ		Uz =750V
numer pomiaru	wartość mierzonego napięcia sieciowego	błąd graniczny woltomierza	Odchylenie pojedynczego pomiaru od średniej
i	Ui	ΔgU
-	V	V	V
1	221,05	0,0815	0,16
2	220,90			0,01
3	221,32			0,43
4	220,80			-0,09
5	220,56			-0,33
6	220,62			-0,27
7	221,44			0,55
8	221,00			0,11
9	221,27			0,38
10	221,37			0,48
11	220,87			-0,02
12	220,81			-0,08
13	220,43			-0,46
14	221,21			0,32
15	220,96			0,07
16	220,16			-0,73
17	221,07			0,18
18	221,33			0,44
19	221,39			0,50
20	220,55			-0,34
21	220,80			-0,09
22	220,90			0,01
23	220,48			-0,41
24	220,68			-0,21
25	220,63			-0,26
26	220,43			-0,46
27	221,18			0,29
28	220,83			-0,06
29	220,48			-0,41
30	221,13			0,24
wartość średnia	=220,89V
odchylenie standardowe			σ = 0,3343V
odchylenie standardowe średniej			=0,0621V

Wartość średnia:

Odchylenie standardowe: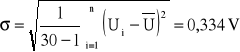

Odchylenie standardowe średniej:

Obliczanie dokładności pomiaru

Z wykonanych obliczeń wynika, że błędy systematyczne i przypadkowe mają porównywalne wartości, czyli błąd graniczny pomiaru wynika z zależność

,

w której: Δ_g(U) - błąd graniczny woltomierza;
- odchylenie standardowe średniej.

W pomiarach stosowano woltomierza HP 34402, którego błąd graniczny określa zależność: 0,02%U_x+0,005%U_z, więc

Ostatecznie

Wynik pomiaru U= (220,89 ± 0,27)V , p=0,997

Błąd względny pomiaru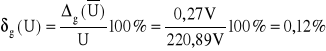

Histogram: Wynik pojedynczego pomiaru napięcia U_i jest realizacją zmiennej losowej (inaczej: zdarzeniem losowym). Zbiór wyników pomiarów tworzy próbę. Po wykonaniu wszystkich pomiarów należy ustalić realizację zmiennej losowej U_i w kolejności rosnącej. Ujawnia się wówczas zakres zmienności zmiennej losowej U
. W rozpatrywanym przykładzie jest <220,16V, 221,44V>. Dla wykonania histogramu, czyli wykresu częstości występowania wyników, zakres ten należy podzielić na nieparzystą liczbę przedziałów (podzakresów) o równej szerokości:

Przedział środkowy przyjąć za obustronnie domknięty.

Tab. 2. Podział zakresu wartości wyników pomiarów na podzakresy

	A	B	C
	Podzakresy	CZĘSTOŚCI WYSTĘPOWANIA	PRAWDOPODOBIEŃSTWO
Numer podzakresu	...,<Uimin+1, Uimin+2),...	Częstość występowania Ui w próbie, dla posortowanych przedziałów	Prawdopodobieństwo występowania Ui w poszczególnych przedziałach
1	<220,16... 220,30)	1	1/30
2	<220,30... 220,44)	2	2/30
3	<220,44... 220,59)	4	4/30
4	<220,59... 220,73)	3	3/30
5	<220,73... 220,87>	5	5/30
6	(220,87... 221,01>	4	4/30
7	(221,01... 221,16>	3	3/30
8	(221,16... 221,30>	3	3/30
9	(221,30... 221,44>	5	5/30
	suma	30	1