Dominika Kobiałka

C3 2004-03-09

L5

Pomiar momentu bezwładności wahadła Maxwella

Bryłę sztywną - ciało można podzielić na tak bardzo małe elementy że można je w przybliżeniu uważać za punkty materialne. Wzajemna odległość promienia dowolnych dwóch punktów A i B jest stała w czasie. W mechanice klasycznej ważną role odgrywa zasada zachowania energii mechanicznej. Jeżeli układ potraktujemy jako układ zamknięty ( odosobniony ) to w miarę ruchu elementów tego układu może nastąpić przemiana energii potencjalnej ciężkości na energię kinetyczną ruchu postępowego i obrotowego lub odwrotnie. Jako przykład zamiany tych energii między sobą może posłużyć Wahadło Maxwella które składa się z krążka osadzonego na osi która jest zawieszona poziomo na dwóch niciach. Nawijając nić na oś podnosimy krążek na wysokość „h” a tym samym gromadzimy w nim energię potencjalną „mgh”. Gdy puścimy krążek wówczas zostaje on wprowadzony w ruch postępowy i obrotowy rośnie a potencjalna energia maleje. Po osiągnięciu najniższego położenia znacznie on podnosić się w górę i wówczas energia kinetyczna przekształca się w energią potencjalną. Proces ten będzie się wielokrotnie powtarzał, jednak w wyniku działania czynników hamujących ruch głównie sił tarcia - wahadło po pewnym czasie zatrzymuje się. Energia krążka składa się z dwóch członów:

-
- energii kinetycznej ruchu postępowego,

-
- energii kinetycznej ruchu obrotowego.

Zasada zachowania energii, przy zaniedbaniu oporów ruchu, wyraża się więc równaniem mgh =
+
gdzie: v - prędkość przesuwania się środka masy układu,

r - promień krążka,

- prędkość kątowa w ruchu obrotowym wokół osi krążka,

I - moment bezwładności krążka względem osi obrotu przechodzącej przez środek masy.

Jeżeli założymy, że ruch środka masy krążka jest ruchem jednostajnie przyspieszonym, bez prędkości początkowej, to z równań:

V = at i h =

otrzymujemy związek:

v =

Po przekształceniu równania:

mgh =
+

względem I i podstawieniu do niego z przytoczonych zależności v i ω wyliczamy moment bezwładności wahadła Maxwella:

I = mr² [
- 1 ]

Wykonanie cwiczczenia

1. Włączyć przyrząd do sieci.

2. Na krążek wahadła nakładam wybrany pierścień i dociskam go do oporu

3. Nawijam na wahadło sznurek a tym samym „wahadło unosi się do góry” i unieruchamiam go przy pomocy elektromagnesu

4. Sprawdzam czy dolna część pierścienia nałożonego na krążek pokrywa się z zerem na skali naniesionej na kolumnę.

5. Naciskam przełącznik w celu wyzerowania przyrządu a następnie wciskam przełącznik W₂ w tym momencie wahadło opuszcza zaciski elektromagnesu i zaczyna się kręcić i przemieszcza się do dołu.

6. gdy osiąga najniższą wartość zostaje pierścień złapany przez fotokomórkę która liczy czas jaki potrzebuje na opadnięcie. Odczytuję wartość zmierzoną spadania wahadła

7. Pomiar powtarzam dziesięć razy, w celu wyznaczenia wartości średniej.

8. po wykonaniu pomiarów biorę kolejny pierścień i tak samo z nim postępuję czyli wyznaczam jego spadek z wysokości h

Moment bezwładności można wyznaczyć w taki sposób traktując wahadło jako współrzędne walca i krążka. Poszczególne momenty bezwładności są średnim momentem bezwładności tego ciała.

Obliczenia

I = I₀ + I_k + I_p

I_o =
m₀r₀²

I_k =
m_k( r_k² + r₀² )

I_p =
m_p( r_p² + r_k² )

Gdzie: r₀ - promień osi wahadła,

r_k - promień zewnętrzny krążka,

r_p - promień zewnętrzny pierścienia.

m0	mk	mp	r	H	t	Idoś	Iteor	Δ
[ g ]	[ g ]	[ g ]	[ cm ]	[ cm ]	[ s ]	[ kg m^2]	[ kg m^2]	%
32.5	124	389,1	5,25	37,4	2,153	0,025		74,92
32.5	124	389,1	5,25	37,4	2,155	0,025		59,85
32.5	124	389,1	5,25	37,4	2,139	0,025		48,75
32.5	124	389,1	5,25	37,4	2,163	0,025	0,0012	60,25
32.5	124	389,1	5,25	37,4	2,142	0,025		59,56
32.5	124	389,1	5,25	37,4	2,139	0,025		59,53
32.5	124	389,1	5,25	37,4	2,120	0,025		58,67
32.5	124	389,1	5,25	37,4	2,130	0,025		57,26
32.5	124	389,1	5,25	37,4	2,112	0,025		58,28
32.5	124	389,1	5,25	37,4	2,136	0,025		58,57
32.5	124	517.0	5,25	37,4	2,213	0,01090		66,74
32.5	124	517.0	5,25	37,4	2,181	0,01059		64,57
32.5	124	517.0	5,25	37,4	2,214	0,01091		66,86
32.5	124	517.0	5,25	37,4	2,192	0,01069	0,001420	65,24
32.5	124	517.0	5,25	37,4	2,194	0,01071		65,43
32.5	124	517.0	5,25	37,4	2,249	0,01126		69,27
32.5	124	517.0	5,25	37,4	2,277	0,01799		11,66
32.5	124	517.0	5,25	37,4	2,239	0,01115		68,54
32.5	124	517.0	5,25	37,4	2,217	0,01094		67,45
32.5	124	517.0	5,25	37,4	2,288	0,01165		72,67

mo + mk+ mp = 54,56

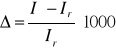
Wnioski :

Na podstawie analizy wyników możemy stwierdzić że ćwiczenie nie zostało wykonane prawidłowo. Za tak wielki błąd pomiarowy , oprócz czynników takich jak niedokładności związane z pomiarem czasu oraz wymiarów poszczególnych części najprawdopodobniej odpowiada uszkodzony elektromagnes

---