Politechnika Śląska w Gliwicach
Wydz. Mechaniczny-Technologiczny
Kierunek :Mechanika i budowa maszyn
SPRAWOZDANIE
Temat: Pomiar prędkości dźwięku w powietrzu .
Solich Jacek
Siwiec Jakub
Pańczak Mariusz
Grupa II
Sekcja III
WPROWADZENIE
Drgające ciało umieszczone w ośrodku sprężystym jest źródłem zaburzenia. Zaburzenie to rozprzestrzenia się w tym ośrodku dzięki sprężystości tego ośrodka .Temu zjawisku towarzyszy przenoszenie energii i pędu przez cząsteczki bez przemieszczania ich średnich położeń . Zjawisko to nazywamy falą .Fala mechaniczna o częstotliwości drgań w zakresie 16Hz - 20kHz ( zakres słyszalności ucha ludzkiego ) nazywa się falą akustyczną .
Prędkość rozchodzenia się fal może zależeć od :
miejsca oraz kierunku rozchodzenia się fali , jeżeli ośrodek jest niejednorodny
(anizotropowy) ; w ośrodku izotropowym prędkość rozchodzenia się fal nie zależy od
miejsca ani kierunku rozchodzenia się fali ,
2) rodzaju fali , tj. od tego czy fala jest podłużna czy poprzeczna ,
3) kierunku drgań w przypadku fal poprzecznych
częstotliwości drgań ; zjawisko zależności prędkości od częstotliwości nazywamy
dyspersją .
Fale sprężyste mogą się rozchodzić jedynie w ośrodkach sprężystych . O tym czy fala sprężysta jest podłużna , czy poprzeczna decydują własności sprężyste ośrodka .
Prędkość rozchodzenia się fali sprężystej jest określona wzorem Newtona
.
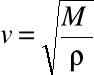
gdzie ,
M - jest odpowiednim modułem sprężystości , - gęstością ośrodka .
Źródło dźwięku wykonując drgania pobudza do drgań cząsteczki otaczającego go powietrza , dając w ten sposób początek fali .
METODA REZONANSOWA.
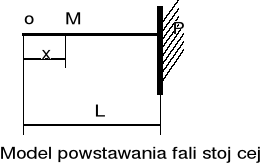
Niech źródło drgań emituje falę płaską harmoniczną w kierunku osi x .
Przeszkoda znajduje się w odległości l . W punkcie M zachodzi superpozycja dwóch fal : bieżącej
![]()
i powracającej po odbiciu od przeszkody. Ta druga fala opóźniona jest w fazie o wielkość
![]()
![]()
, gdzie jest dodatkowym opóźnieniem , które może powstać podczas odbicia od przeszkody .
Równanie tej fali ma więc postać :
![]()
Amplituda otrzymanej fali stojącej
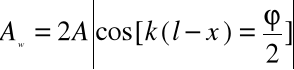
jest okresową funkcją odległości punktu od przeszkody x i nie zależy od czasu .Maksimum fali występuje w punktach o współrzędnej spełniającej warunek :
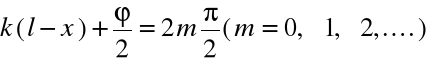
a punkty te nazywamy strzałkami . Dla węzłów , czyli punktów ,w których zanikają drgania , warunek jest następujący :
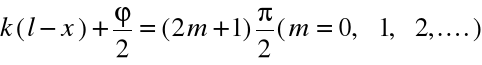
Odległość między sąsiednimi węzłami ( lub strzałkami ) jest równa połówce długości fali 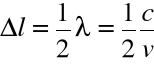
METODA OSCYLOGRAFICZNA
Wewnątrz rury znajdują się głośnik i mikrofon . Głośnik zasilany jest z generatora , natomiast mikrofon jest włączony do wzmacniacza odchylania Y oscylografu . Zmieniając częstotliwość generatora należy doprowadzić do powstania w rurze fali stojącej , co jest realizowane przy spełnieniu warunku
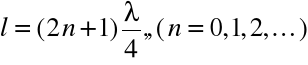
Nie zmieniając położenia mikrofonu należy znaleźć inną ( najbliższą ) częstotliwość , przy której znowu wytworzymy w rurze falę stojącą , a sygnał odbierany przez mikrofon osiągnie maksimum .
Częstotliwość spełnia warunek :
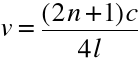
Odejmując stronami dwukrotną realizację powyższego wzoru otrzymamy :
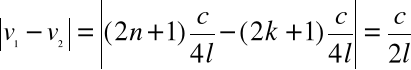
ponieważ k i n różnią się o 1 .
PRZEBIEG ĆWICZENIA
Łączymy obwód wg. schematu :
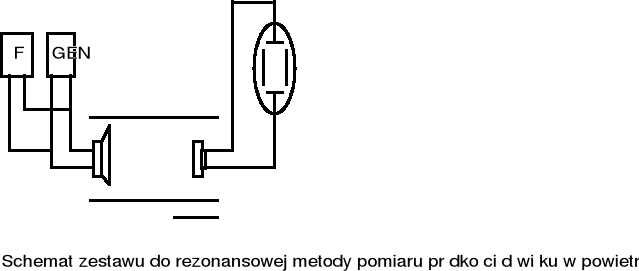
2.Ustalamy częstotliwość i przesuwając mikrofon szukamy położenia odpowiadającego maksymalnemu sygnałowi obserwowanemu na ekranie oscyloskopu .
3.Nie zmieniając położenia mikrofonu szukamy dwóch najbliższych wartości częstotliwości odpowiadających rezonansowi akustycznemu .
4. Pomiary wykonujemy przy trzech różnych położeniach mikrofonu notując każdorazowo 3 częstotliwości rezonansowe.
5. Obliczamy wartości prędkości dźwięku stosując wzór :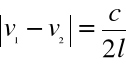
,
gdzie ![]()
![]()
i otrzymane wartości uśredniamy.
6. Przeprowadzamy dyskusję błędów.
METODA PRZESUNIĘCIA FAZOWEGO
Przesunięcie fazowe w punkcie odległym od źródła o x wynosi :
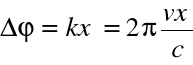
Łączymy obwód wg schematu :
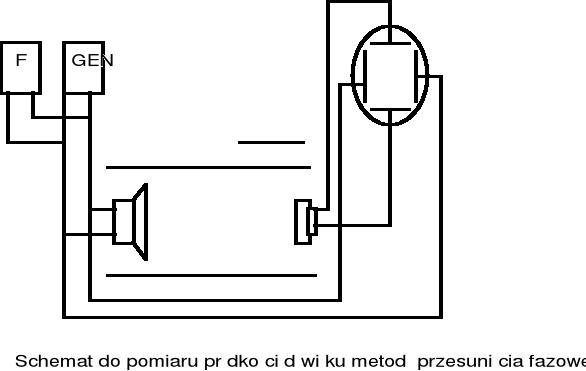
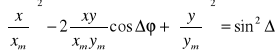
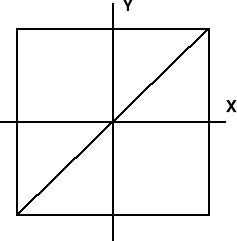
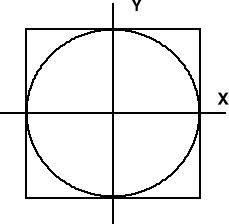
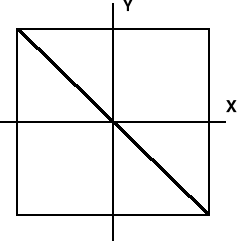
Realizując składanie drgań w płaszczyznach wzajemnie prostopadłych otrzymujemy na ekranie oscyloskopu elipsę , której kształt i nachylenie osi zależy od stosunku amplitud i przesunięcia fazowego :
W poniższej tablicy pokazano przykłady kształtu elips dla kilku wartości przesunięć fazowych .
KSZTAŁT ELIPS W FUNKCJI PRZESUNIĘCIA FAZOWEGO
|
0 |
/4 |
/2 |
3/4 |
|
|
|
|
|
|
|
Nas interesują przypadki najprostsze odpowiadające liniom prostym . Zasada pomiaru polega na znalezieniu takich kolejnych położeń mikrofonu , którym odpowiadają linie proste ( =π ) . Wówczas prędkość dźwięku wyraża wzór :
![]()
gdzie
v - częstotliwość napięcia z generatora .
PRZEBIEG ĆWICZENIA.
1.Przy ustalonej częstotliwości szukamy takich położeń mikrofonu , kiedy na ekranie elipsa przejdzie w prostą skośną .Notujemy takie położenia .
2. Pomiary powtarzamy dla innych częstotliwości .
3.Obliczamy prędkość dźwięku wg. wzoru :
![]()
4. Obliczamy wykładnik adiabaty
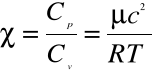
gdzie R = 8.31 J/mol*K - uniwersalna stała gazowa ,
= 28.87*10^-3 kg/mol - masa molowa powietrza ,
T - temperatura powietrza .
5. Przeprowadzamy rachunek błędów .
1
2
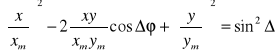
Wyszukiwarka
Podobne podstrony:
Pomiar prędkości dźwięku w powietrzu. Metody rezonansowa i przesunięcia fazowego
Pomiar kata przesuniecia fazowego, fff, dużo
Współczynnika Kappa dla powietrza 2, fff, dużo
Pomiar predkosci dziwieku w powietrzu
Mostek liniowy-Pomiar oporu mostkiem Wheastone, fff, dużo
Wyznaczanie wspolczynnika zalamania swiatla w powietrzu, fff, dużo
Pomiar prędkości dźwięku w powietrzu metodami rezonansową, Quinckego i przesunięcia?zowego
Współczynnika Kappa dla powietrza, fff, dużo
pomiar predkości przepływu powietrza, NAUKA, Politechnika Slaska w Rybniku kierunek Górnictwo i Geo
Pomiar prędkości dźwięku w powietrzu
Karta pom Pomiar predkosci dzwieku w powietrzu jako funkcji temp
Wyznaczanie predkosci dzwieku w powietrzu metoda rezonanso, fff, dużo
pierwsza strona sprawozdania, fff, dużo
FIZYKA 47, fff, dużo
Pomiar wilgotności względnej powietrza przechowalnictwo lab 15
POMIARY PRĘDKOŚCI
Precyzyjne pomiary prędkości radialnych gwiazd
Pomiar prędkości statków log
więcej podobnych podstron