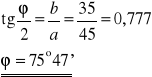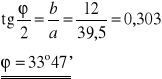Politechnika Śląska w Gliwicach
Wydz. Mechaniczny-Technologiczny
Kierunek :Mechanika i budowa maszyn
SPRAWOZDANIE
Temat: Pomiar kąta przesunięcia fazowego.
Obserwacja krzywych Lissajous.
Solich Jacek
Siwiec Jakub
Pańczak Mariusz
Grupa II
Sekcja III
WPROWADZENIE.
Oscyloskop jest najbardziej uniwersalny przyrządem pomiarowym i kontrolnym. Można wykonać różnorodne pomiary, np. napięcia, natężenia prądu, częstości, fazy itp. Można bezpośrednio obserwować zjawiska elektryczne w funkcji czasu, a także wiele innych zjawisk fizycznych i biologicznych za pomocą odpowiednich przetworników.
Zasadniczą częścią oscyloskopu jest lampa oscyloskopowa. Strumień elektronów wylatujących z działa elektronowego po przejściu przez szereg anod przechodzi przez dwie pary płytek odchylających i uderzając w luminofor ekranu wywołuje na ekranie plamkę świetlną. Poprzez zmianę napięcia na elektrodzie działa uzyskuje się zmienne ostrości plamki, natomiast jaskrawość plamki od potencjału siatki sterującej. Sygnał wejściowy podawany jest do płytek pionowego poprzez tłumnik i wzmacniacz.
Najważniejszymi parametrami oscyloskopu są:
pasmo wzmocnienia - zakres częstości, przy których sygnał wzmacnia się w nim o 3 dB,
czułość - wartość napięcia odpowiadająca wysokości impulsu na ekranie równej 1 cm,
impedancja wejściowa.
Typowa lampa oscyloskopowa składa się ze szklanej , wydłużonej bańki, wewnątrz której znajduje się : działo elektronowe, układ odchylający i ekran. W bańce wytwarza się stosunkowo wysoką próżnię. Uproszczony schemat działa dwuanodowego lampy jednostrumieniowej przedstawiono na rysunku 1.
Rys. 1
![]()
![]()
Prędkość elektronów obliczamy z zasady zachowania energii:
![]()
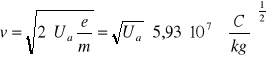
stąd
Dla napięć anodowych większych od 15 kV należy stosować wzory relatywistyczne, uwzględniając zmianę masy elektronu przy zmianie prędkości.
Odchylenie plamki na ekranie lampy jest proporcjonalne do napięcia Uy przyłożonego do płytek odchylenia (w naszym przypadku - pionowego).
W celu obserwacji przebiegów napięcia zmiennego, do płytek odchylenia poziomego doprowadza się napięcie piłokształtnego wytwarzane przez generator podstawy czasu. Liniowe narastanie napięcia podstawy czasu przesuwa plamkę w prawo. Powrót plamki następuje bardzo szybko, ponieważ nachylenie części opadającej jest bardzo duże. Podczas obserwacji przebiegów zmiennych należy zwrócić uwagę na sposób synchronizacji przebiegów przyłożonych do obu par płytek i wyzwolenia podstawy czasu.
POMIAR KĄTA PRZESUNIĘCIA FAZOWEGO.
![]()
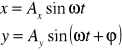
Weźmy dwa drgania harmoniczne o tej samej amplitudzie , lecz różnych fazach i zachodzące w płaszczyznach do siebie prostopadłych:
![]()
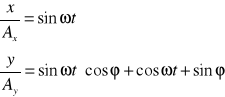
W celu znalezienia równania toru, po którym będzie się przesuwał punkt w wyniku dodania drgań należy z powyższych równań wyeliminować czas. Zapiszemy powyższe równania w postaci:
Pomnóżmy równanie (3) przez cosϕ i odejmijmy od równania (4),a otrzymaną różnicę podnieśmy do kwadratu:
![]()
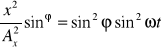
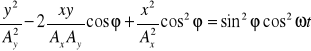
![]()
Pomnóżmy równanie (5) przez sinϕ i podnieśmy do kwadratu:
![]()
Po dodaniu stronami dwóch ostatnich równań i skorzystaniu z „jedynki trygonometrycznej” otrzymamy ostatecznie:
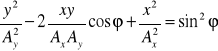
Otrzymaliśmy równanie elipsy o środku w punkcie [0,0]. Orientacja półosi zależy od kąta przesunięcia fazowego.
![]()
Kąt przesunięcia fazowego można wyznaczyć, jeśli znamy współrzędne przecięcia elipsy z osiami układu współrzędnych. Jeśli w równaniu (9) wstawimy x=0, to:
![]()
![]()
gdzie ym=Ay - amplituda drgań w płaszczyźnie OY. A y) -rzędna dla x=0.
![]()
Podobnie dla y=0 otrzymamy:
![]()
![]()
Jeśli ustalimy równość amplitud obydwu drgań, to równanie (9) może przyjąć postać kanoniczną:
gdzie a i b są długościami półosi elipsy.
PRZEBIEG ĆWICZENIA
Łączymy obwód wg schematu podanego na rysunku nr 2.
Rys.2
Realizujemy kolejno układy przesuwników fazowych zmieniając kondensatory i rezystory.
Ustalamy wielkości elipsy mieszczącej się w kwadracie o boku 8 cm.
Obraz elipsy przenosimy na folię.
Pomiary powtarzamy dla wszystkich kombinacji połączeń R i C.
Obliczamy wartości kąta przesunięcia fazowego metodami:
analityczną,
półosi elipsy,
rzędnych lub odciętych.
Przeprowadzamy rachunek błędów.
OBSERWACJA KRZYWYCH LISSAJOUS.
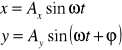
Krzywe Lissajous pochodzą ze złożenia wzajemnie prostopadłych drgań harmonicznych o jednakowych amplitudach lecz różnych częstotliwościach i różnych wartościach różnicy faz ϕ pomiędzy nimi.
Stosunkowo prosto znajduje się te krzywe w przypadku, gdy stosunek częstości składanych drgań jest stosunkiem małych liczb naturalnych
Stosując konstrukcję geometryczną można znaleźć kształt takiej krzywej. Kształt krzywej zależy od stosunku częstości i przesunięcia fazowego składanych drgań.
PRZEBIEG ĆWICZENIA.
Łączymy obwód wg schematu pokazanego na rysunku nr 3.
Rys.3
ustalamy wzmocnienie Y-Y oraz napięcie wyjściowe generatora tak, aby na ekranie oscyloskopu otrzymać obraz odpowiedniej wielkości.
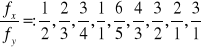
Obserwujemy kształt figur dla stosunku częstości:
Po ustaleniu optymalnie stabilnego obrazu przenosimy go na folię.
Mierzymy częstotliwość sieciową fy.
Metodą przecięć obliczamy częstotliwość napięcia na wyjściu generatora fx.
Rysujemy krzywą skalowania generatora fxs = f(fx), gdzie fxs jest częstotliwością odczytaną ze skali generatora.
Obserwacja krzywych Lissajous - opracowanie wyników pomiarów.
Obserwacja krzywych Lissajous
fy = 50Hz
L.p. |
Fxs [Hz] |
Fs [Hz] |
1 |
52 |
|
2 |
27 |
|
3 |
100 |
|
4 |
19 |
|
5 |
76 |
|
6 |
150 |
|
![]()
Pomiar I.
![]()
![]()
![]()
Pomiar II.
![]()
Pomiar III.
![]()
![]()
Pomiar IV.
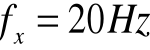
Pomiar V.
![]()
![]()
![]()
Pomiar VI.
![]()
L.p. |
Fxs [Hz] |
Fs [Hz] |
1 |
52 |
50 |
2 |
27 |
25 |
3 |
100 |
100 |
4 |
19 |
20 |
5 |
76 |
75 |
6 |
150 |
350 |
Pomiar VI odrzucamy ze względu na duży błąd pomiaru.
POMIAR KĄTA PRZESUNIĘCIA FAZOWEGO - OPRACOWANIE WYNIKÓW POMIATÓW.
Pomiar kąta przesunięcia.
L.p. |
R [kΩ] |
C [μF] |
Typ* |
Półosie [mm] |
|
Współrzędne [mm] |
|
|
|
|
|
|
|
a |
b |
x0 |
xm |
y0 |
ym |
1 |
15 |
1 |
a |
|
|
|
|
|
|
2 |
15 |
47 |
a |
|
|
|
|
|
|
3 |
47 |
1 |
a |
|
|
|
|
|
|
4 |
47 |
47 |
a |
|
|
|
|
|
|
* - podaj typ przesuwnika fazowego (a - całkujący, b - różniczkujący)
POMIAR I.
L.p. |
R [kΩ] |
C [μF] |
Typ* |
Półosie [mm] |
|
Współrzędne [mm] |
|
|
|
|
|
|
|
a |
b |
x0 |
xm |
y0 |
ym |
|
15 |
1 |
a |
45 |
35 |
40 |
40 |
36,5 |
37 |
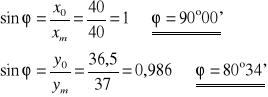
Obliczamy średnią arytmetyczną wartość ϕ :
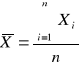
- wartość poprawna
ϕ = 82°6'
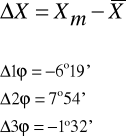
Obliczamy błąd bezwzględny:
Obliczamy błąd średni kwadratowy:
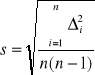
![]()
A więc można zapisać:
![]()
POMIAR II.
L.p. |
R [kΩ] |
C [μF] |
Typ* |
Półosie [mm] |
|
Współrzędne [mm] |
|
|
|
|
|
|
|
a |
b |
x0 |
xm |
y0 |
ym |
|
15 |
1 |
a |
39,5 |
12 |
13,5 |
14 |
34 |
39,5 |
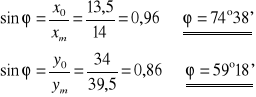
Obliczamy średnią arytmetyczną wartość ϕ :
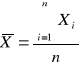
- wartość poprawna
ϕ = 55°54'
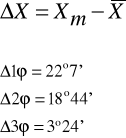
Obliczamy błąd bezwzględny:
Obliczamy błąd średni kwadratowy:
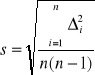
![]()
A więc można zapisać:
![]()
POMIAR III.
L.p. |
R [kΩ] |
C [μF] |
Typ* |
Półosie [mm] |
|
Współrzędne [mm] |
|
|
|
|
|
|
|
a |
b |
x0 |
xm |
y0 |
ym |
3 |
15 |
1 |
a |
37,5 |
8 |
8 |
10 |
28,5 |
35 |
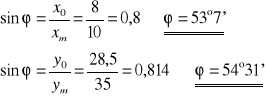
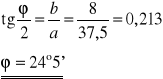
Obliczamy średnią arytmetyczną wartość ϕ :
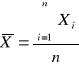
- wartość poprawna
ϕ = 37°32'
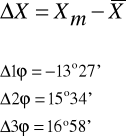
Obliczamy błąd bezwzględny:
Obliczamy błąd średni kwadratowy:
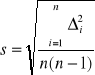
![]()
A więc można zapisać:
![]()
POMIAR IV.
L.p. |
R [kΩ] |
C [μF] |
Typ* |
Półosie [mm] |
|
Współrzędne [mm] |
|
|
|
|
|
|
|
a |
b |
x0 |
xm |
y0 |
ym |
4 |
15 |
1 |
a |
52 |
17 |
22,5 |
39 |
24 |
40 |
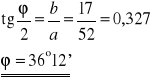
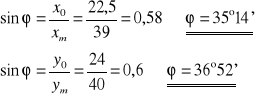
Obliczamy średnią arytmetyczną wartość ϕ :
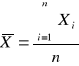
- wartość poprawna
ϕ = 36°6'
Obliczamy błąd bezwzględny:
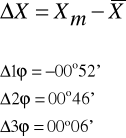
Obliczamy błąd średni kwadratowy:
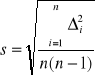
![]()
A więc można zapisać:
![]()
ZESTAWIENIE WYNIKÓW
L.p. |
R [kΩ] |
C [μF] |
Typ* |
Półosie [mm] |
Współrzędne [mm] |
ϕ |
||||
|
|
|
|
a |
b |
x0 |
xm |
y0 |
ym |
|
1 |
15 |
1 |
a |
45 |
35 |
40 |
40 |
36,5 |
37 |
82o06' ± 04o10' |
2 |
15 |
47 |
a |
39,5 |
12 |
13,5 |
14 |
34 |
39,5 |
55o54' ± 11o54' |
3 |
47 |
1 |
a |
37,5 |
8 |
8 |
10 |
28,5 |
35 |
37o32' ± 10o53' |
4 |
47 |
47 |
a |
52 |
17 |
22,5 |
39 |
24 |
40 |
36o06' ± 00o13' |
14
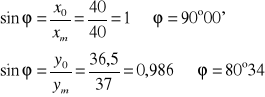
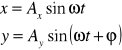
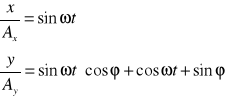
![]()
![]()
![]()
![]()
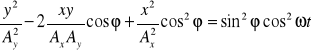
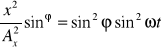
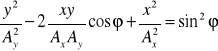
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
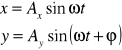
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
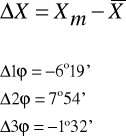
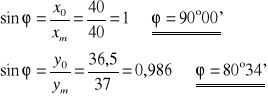
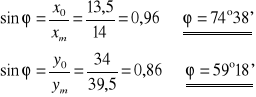
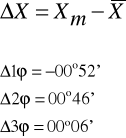
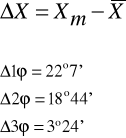
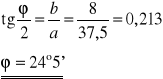
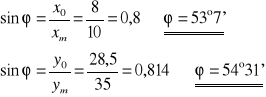
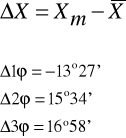
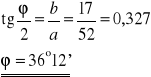
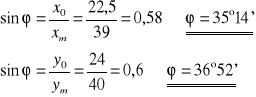
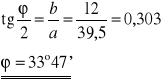
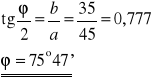
Wyszukiwarka
Podobne podstrony:
Pomiar predkosci dzieku w powietrzu, fff, dużo
Miernictwo - Pomiar częstotliwości i przesunięcia fazowego, Sprawolki
Pomiar czestotliwosci i przesuniecia fazowego sygnalow okresowych
Sprawozdania przerobione, Pomiary częstotliwości i przesunięcia fazowego sygnałów okresowych 1, Wska
wyklad 07 cd z tej-strony-co-podala-frania, POMIARY CZĘSTOTLIWOŚCI I PRZESUNIĘCIA FAZOWEGO SYGNAŁÓW
Pomiar Częstotliwości i przesunięcia fazowego, Szkoła, penek, Przedmioty, Fizyka, Laborki
Mostek liniowy-Pomiar oporu mostkiem Wheastone, fff, dużo
Pomiar częstotliwości i przesunięcia fazowegio, Fizyka sprawka
ćw 7 Pomiary Czestotliwości i Przesunięcia Fazowego
Pomiar częstotliwości i przesunięcia fazowego 2003 10 19
Pomiar przesunięcia fazowego w obwodzie prądu przemiennego, FIZA 205
pomiar czŕstotliwoťci i przesuniŕcia fazowego
Pomiar prędkości dźwięku w powietrzu. Metody rezonansowa i przesunięcia fazowego
Pomiar przesunięcia fazowego w obwodzie prądu przemiennego, FIZA20~1, Nr.205
Pomiary przesunięcia fazowego
01 Pomiar przesuniecia fazowegoid (2)
Pomiar przesunięcia fazowego w obwodzie prądu przemiennego, 205, Nr.205
więcej podobnych podstron