POLITECHNIKA ŚLĄSKA

w GLIWICACH

wydz. Elektryczny

studia dla pracujących

1997/98

sem.4

Temat: POMIAR CZĘSTOTLIWOŚCI I PRZESUNIĘCIA FAZOWEGO

Wprowadzenie.

Pojęcie częstotliwości związane jest z sygnałem okresowym. Najmniejszy przedział czasu, po którym obserwowany sygnał powtarza się nazywamy okresem i oznaczamy symbolem T.

Warunek okresowości możemy więc zapisać:

f (t) = f ( t + T )

Częstotliwością nazywamy odwrotność okresu i oznaczamy symbolem f = 1/T. Wyraża ona liczbę cykli sygnału okresowego zachodzących w jednostce czasu (s). Jednostką częstotliwości jest 1 Hz.

Sinusoidalny sygnał okresowy można przedstawić jako rzut wektora wirującego na płaszczyźnie zespolonej na oś liczb urojonych.

Kąt  zawarty między osią liczb rzeczywistych a wirującym wektorem w chwili t nazywamy fazą sygnału. Wektor wirujący można opisać zależnością trygonometryczną:

W(t) = A (cost + j sint)

gdzie: A-długość wektora ( amplituda sygnału )

 = 2 / T - pulsacja sygnału

Rzut wektora na oś liczb urojonych jest sygnałem sinusoidalnym:

s(t) = Im {W(t)} = A sint

Różnicę faz dwóch sygnałów sinusoidalnych nazywamy przesunięciem fazowym.

Aby przesunięcie fazowe było stałe w czasie prędkości kątowe wektorów, a więc i częstotliwości sygnałów muszą być jednakowe. Jeżeli częstotliwości sygnałów są różne, przesunięcie fazowe zmienia się liniowo w czasie i wynik pomiaru zależy od chwili jego wykonania.

Przesunięcie fazowe można wyznaczyć znając prędkość kątową wektorów  oraz czas t­₀ jaki upływa między przejściem pierwszego i drugiego wektora przez oś liczb rzeczywistych, korzystając z zależności:

 = t₀ = 2f t₀

Powyższa zależność traci ważność dla sygnałów odkształconych, dla których należy mierzyć przesunięcia fazowe pomiędzy poszczególnymi harmonicznymi ( z wykorzystaniem specjalnych filtrów ).

Metody pomiaru częstotliwości.

Metoda oscyloskopowa.

Pomiar częstotliwości za pomocą oscyloskopu polega na porównaniu napięcia o badanej częstotliwości f_x z napięciem o częstotliwości wzorcowej f_w. Pomiar polega na doprowadzeniu do jednej pary płytek odchylających oscyloskopu, napięcia o nie znanej częstotliwości f_x, napięcie o częstotliwości wzorcowej f_w z przestrajanego generatora wzorcowego doprowadzamy do drugiej pary płytek odchylających. Kształt krzywej na ekranie (tzw. figury Lissajous) zależy od kształtu doprowadzonych napięć (najczęściej sinusoidalne), od stosunku częstotliwości f_x/f_w napięcia mierzonego do wzorcowego oraz ich wzajemnego przesunięcia fazowego .

W przypadku gdy stosunek częstotliwości f_x/f_y jest równy stosunkowi liczb całkowitych, obraz na ekranie pozostaje nieruchomy. Częstotliwość f_x najłatwiej wyznaczyć metodą siecznych, prowadząc dwie prostopadłe sieczne, jedną równoległą do osi X-prosta a, drugą równoległą do osi Y-prosta b. Jeżeli k_y będzie liczbą przecięć nieruchomej figury Lissajous przez sieczną b, a k_x liczbą przecięć przez sieczną a, to wtedy zachodzi:

gdzie: f_x i f_y - częstotliwości napięć przyłożonych do płytek X i Y oscyloskopu.

Aby uzyskać prawidłowy wynik pomiaru otrzymana figura powinna być nieruchoma, w tym przypadku dokładność pomiaru może być równa dokładności użytego generatora wzorcowego.

Metoda cyfrowa.

Cyfrowy pomiar częstotliwości polega na zliczaniu liczby cykli przebiegu okresowego w określonym czasie. Uzyskanie dostatecznej dokładności pomiaru małych częstotliwości wymaga zwiększenia czasu zliczania (np. 100 lub 1000 s.) a tym samym czasu pomiaru.

W takim przypadku dokonujemy pomiaru okresu, skąd pośrednio można wyznaczyć częstotliwość. Mierniki do pomiaru okresu posiadają takie same bloki funkcjonalne jak mierniki do pomiaru częstotliwości, dlatego najczęściej produkowane są mierniki do pomiaru obu tych wielkości ( częstościomierze - okresomierze ).

Przy pomiarze częstotliwości przełączniki a i b znajdują się w pozycji „1”. Napięcie okresowe o mierzonej częstotliwości f_x przetwarzane jest w układzie formującym na przebieg prostokątny, który doprowadzany jest do wejścia bramki. Napięcie z generatora wzorcowego o okresie T_x przekształcane jest przez przerzutnik (wyzwalany narastającymi zboczami sygnału wzorcowego) w sterujący impuls prostokątny „st” o czasie trwania T­_w, otwierający bramkę. W czasie otwarcia bramki zliczane są narastające (lub opadające) zbocza przebiegu prostokątnego doprowadzonego z układu formującego. Po zamknięciu bramki liczba N zliczona przez licznik jest równa iloczynowi częstotliwości f_x i czasu otwarcia bramki T_w:

N = f_x T_w

stąd:

Przy pomiarze okresu T_x przełączniki a i b znajdują się w pozycji „2” (na rys. oznaczenia w nawiasach). Napięcie okresowe o mierzonym okresie T_x przetwarzane jest w układzie formującym na przebieg prostokątny, który przerzutnik formujący zmienia na prostokątny impuls sterujący „st”. Otwiera on bramkę na czas T_x. Do wejścia bramki doprowadzony jest przebieg prostokątny z generatora wzorcowego o częstotliwości f_w. W czasie otwarcia bramki zliczane są narastające zbocza prostokątnego przebiegu doprowadzanego z generatora wzorcowego. Po zamknięciu bramki liczba N zliczona przez licznik równa iloczynowi częstotliwości f_w i czasu otwarcia bramki T_x:

N = T_x f_w

stąd:

Błąd cyfrowego pomiaru okresu lub częstotliwości składa się z trzech elementarnych błędów:

δ = δ_w + δ _b + δ_N

gdzie: δ_w - błąd względny wzorca, wynikający z różnicy między nominalną i rzeczywistą

wartością częstotliwością wartością częstotliwości wzorcowej f_w (lub okresu T_w).

δ_b - błąd względny bramkowania, wynikający z różnicy opóźnień czasu otwarcia i

zamknięcia bramki. Błąd ten przyjmuje wartość zerową jeżeli czas opóźnienia otwarcia i zamknięcia bramki jest taki sam.

δ_N - błąd dyskretyzacji (kwantowania), wynika z przekształcenia wartości ciągłej w

dyskretną. Maksymalna wartość bezwzględna tego błędu jest równa jedności na

najmniej znaczącej pozycji wskazywanej liczby i wynika ona z pominięcia cyfr na

dalszych nie wskazywanych pozycjach. Względny błąd dyskretyzacji dla

wskazywanej liczby N jest równy jej odwrotności.

Błędy wzorca i bramkowania sprowadza się konstrukcyjnie do takiej wartości, aby ich suma była mniejsza od błędu dyskretyzacji, wtedy niepewność względna pomiaru wyraża się wzorem:

Metody pomiaru przesunięcia fazowego.

Metoda sumowania napięć.

Geometryczna suma lub różnica dwóch napięć sinusoidalnych jest zależna od przesunięcia fazowego między nimi.

Dla geometrycznej różnicy wektorów napięcia otrzymujemy

równanie:

U_r² = U₁² + U₂² - 2U₁U₂cos

stąd:

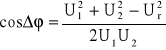
jeżeli moduły napięć są sobie równe to:

ponieważ :

1-cos = 2 sin²(/2)

więc:

sin(/2) = U_r/(2U)

Dla sumy geometrycznej otrzymujemy następujące zależności:

cos = (U_s²/2U²) - 1

lub:

cos(/2) = U_s/2U

Metodą sumowania napięć możemy wyznaczyć przesunięcie fazowe w zakresie 0  180. Jednak błąd wyznaczenia  w zakresie 0  90 jest mniejszy przy pomiarze różnicy napięć, a dla a dla kątów większych - sumy napięć. Metoda ta określa tylko moduł przesunięcia fazowego. Jeżeli nie znamy znaku przesunięcia fazowego, należy do jednego z napięć wprowadzić przesunięcie fazowe o znanym znaku i stąd wnioskować o znaku mierzonego przesunięcia fazowego.

Metoda oscyloskopowa.

Oscyloskopowy pomiar przesunięcia fazowego wykorzystuje właściwości krzywych Lissajous powstających na ekranie oscyloskopu, gdy do torów odchylania X i Y doprowadzane są napięcia sinusoidalne o tej samej częstotliwości. Lecz przesunięte w fazie. Odchylanie w osi poziomej jest równe:

x = S_x u_x = S_x A sint

natomiast w osi pionowej:

y =S_y u_y = S_y B sint

gdzie : S_x, S_y - czułości torów odchylania X, Y.

Po przekształceniu powyższych zależności otrzymujemy:

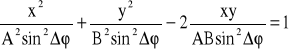
podstawiając do powyższej zależności wartość x=0 lub y=0 i przekształcając otrzymujemy:

sint = x₀/A = y₀/B

Zależność tą stosuje się do wyznaczania przesunięcia fazowego dla <60. Dla kątów zawartych w zakresie 6090 większą dokładność uzyskuje się przesunięcie fazowe metodą tangensa: tg(/2) = b/a

gdzie: a - dłuższa, b - krótsza oś elipsy

Wyznaczenie wartości przesunięcia fazowego  sprowadza się do pomiarów geometrycznych obrazu na ekranie lampy oscyloskopowej

Metoda oscyloskopowa również określa tylko moduł przesunięcia fazowego.

Metoda cyfrowa.

Metoda ta polega na cyfrowym pomiarze przesunięcia czasowego t₀ i obliczeniu przesunięcia fazowego wprost z definicji:

 = t₀ = 2f t₀

Pomiar taki może być wykonany za pomocą częstościomierza - czasomierza cyfrowego.

Rys. schemat blokowy układu do pomiaru przesunięcia fazowego metodą cyfrową.

Sygnały napięciowe u₁(t) oraz u₂(t) doprowadzane są na wejścia układów formujących. Efektem formowania jest napięcie o przebiegu prostokątnym, przyjmującym wartości dodatnie dla sygnałów większych od zera i ujemne dla sygnałów mniejszych od zera. Uformowane napięcia doprowadzane są do układu sterowania bramką, który otwiera bramkę narastającym zboczem uformowanego sygnału U₁, a następnie zamyka narastającym zboczem uformowanego sygnału U₂. W czasie otwarcia bramki licznik zlicza impulsy z pomocniczego generatora wzorcowego. Liczba N zliczonych impulsów jest miarą przesunięcia czasowego t₀, a więc:

t₀ = N/f_w = N T_w

gdzie: f_w - częstotliwość wzorcowa, T_w = 1/f_w

Następnie należy dokonać pomiaru częstotliwości f lub okresu T i wyznaczamy przesunięcie fazowe:

 = 360f t₀ = 360(t_0­/T)

Mierząc przesunięcie czasowe t₀ i okres przy tej samej częstotliwości generatora wzorcowego, możemy wyznaczyć przesunięcie fazowe ze stosunku zliczonych impulsów:

 = 360(N t_w/N_T t_w) = 360(N_­/N_T)

gdzie: N_T - liczba impulsów zliczona przy pomiarze okresu.

Dokładność pomiaru przesunięcia fazowego metodą cyfrową zależy od błędu pomiaru przesunięcia czasowego t_0­­, jak i okresu T. Błąd pomiaru okresu wyznacza się tak jak przy pomiarze okresu metodą cyfrową.

Na całkowity błąd pomiaru przesunięcia czasowego t₀ nakładają się trzy składniki:

• Błąd formowania - wynikający z niestałości poziomu zerowego układów formujących. Zbocza uformowanego sygnału prostokątnego nie pojawiają się w chwili, gdy sygnał wejściowy ma wartość zero, ale po osiągnięciu pewnej wartości u. Przesunięcie poziomu u może mieć wartość dodatnią lub ujemną. Zatem zbocze formowanego sygnału prostokątnego może pojawić się przed, jak i po przejściu sygnału wejściowego przez zero. Powoduje to zmianę czasu otwarcia bramki przez jeden układ formujący, jak i jej zamknięcia przez drugi.

• Błąd dyskretyzacji - równy odwrotności zliczonych impulsów N. Błąd ten rośnie z częstotliwością, ponieważ przy tej samej wartości przesunięcia fazowego  maleje t₀, a tym samym liczba impulsów N. Przy cyfrowym pomiarze przesunięcia fazowego wartość tego błędu ogranicza górny zakres częstotliwości do kilkudziesięciu kHz.

• Błąd wzorca czasu t_w - z powodu znikomej wartości (rząd 10^-9) można go pominąć.

Metodą cyfrową możemy mierzyć przesunięcia fazowe pomiędzy podstawowymi składowymi przebiegów odkształconych, jeżeli ich rozkłady na szeregi Fouriera mają postać:

lub

a ich przebiegi czasowe nie posiadają więcej niż dwóch przejść przez zero w czasie okresu T.

Wyniki pomiarów i obliczenia.

1. Pomiar częstotliwości.

Lp.	f [Hz]	tp=0,1s fx [*10^3Hz]	tp=1s fx [Hz]	tp=10s fx [Hz]	δfx = (1/N)*100[%]
										tp=0,1s	tp=1s	tp=10s
1	1		2	2,0		50	5
2	10	0,02	11	11,0	50	9,09	0,91
3	100	0,11	101	101,0	9,09	1	0,1
4	1000	1,00	1001	1000,2	1	0,1	0,01
5	10000	10,00	9995	9994,0	0,1	0,01	0,001
6	100000	99,24	99236	99238,0	0,01	0,001	0,0001

2. Pomiar okresu.

Lp.	f [Hz]	Tx [ms]			10* Tx [ms]
				fw=100kHz	fw=1MHz	fw=10MHz	fw=100kHz	fw=1MHz	fw=10MHz
1	1	980,80	998,336	998,5980	9985,60	9985,580	9931,1500
2	10	100,30	100,288	100,3114	1003,02	1003,048	1003,0436
3	100	9,12	9,121	9,1204	91,22	91,211	91,2203
4	1000	0,99	0,992	0,9915	9,92	9,915	9,9155
5	10000	0,10	0,100	0,1001	1,00	1,000	1,0005
6	100000	0,01	0,011	0,0101	0,10	0,101	0,1008

Uwaga: w trakcie pomiarów dla niskich częstotliwości ( 1 - 10 Hz) uzyskaliśmy zaniżone

wartości T_x. Może to być spowodowane układem wyzwalającym otwierającym

bramkę na czas T_x/2 (układ mierzy w tym przypadku połowę okresu). W tabeli powyżej wartości te są pomnożone dwukrotnie.

Niepewność wyznaczania okresu.

Lp.	δTx [%]
		tp=Tx			tp=10Tx
1	0,001	0,0001	0,00001	0,00001	0,000001	0,0000001
2	0,01	0,001	0,0001	0,0001	0,00001	0,000001
3	0,11	0,011	0,0011	0,0011	0,00011	0,000011
4	1,012	0,101	0,0101	0,0101	0,00101	0,000101
5	10	1	0,0999	0,1	0,01	0,001
6	100	9,1	0,9901	1	0,09901	0,01

δ_Tx = (1/N)*100

wartości δ_Tx dla t_p=10T_x są niepewnościami pomiaru jednego okresu:

δ_Tx = (1/N)*10

Pomiar częstotliwości metodą oscyloskopową.

Dla częstotliwości wzorcowej f_w=10 [Hz] doprowadzonej do poziomego toru odchylania oscyloskopu.

a)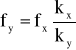

k_x = 2

k_y = 2

f_y = f_x = 10 [Hz]

b)

k_x = 2

k_y = 4

f_y = ½ f_x = 5 [Hz]

Wnioski.

W przypadku pomiaru częstotliwości metodą cyfrową niepewność względna pomiaru maleje dekadowo wraz ze wzrostem częstotliwości badanego sygnału oraz czasu trwania pomiaru. Częstotliwościomierze cyfrowe należy stosować więc do pomiaru częstotliwości f_x>>1/T_w , (1/T_w - częstotliwość sygnału sterującego otwarciem bramki).

Dla pomiaru okresu metodą cyfrową obserwujemy sytuację odwrotną, niepewność pomiaru rośnie wraz ze spadkiem czasu trwania okresu badanego sygnału (a więc wraz ze wzrostem jego częstotliwości ). Okres badanego sygnału powinien być więc co najmniej dwa rzędy wielkości większy od okresu przebiegu wzorcowego.

Ponieważ błąd dyskretyzacji ma decydujący wpływ na niepewność pomiaru zarówno częstotliwości jak i okresu, należy go minimalizować. W tym celu możemy dla pomiaru częstotliwości zwiększać czas trwania pomiaru, przy pomiarze okresu zwiększać: liczbę mierzonych okresów lub częstotliwość generatora wzorcowego.

Przy pomiarach częstotliwości metodą oscyloskopową durzy wpływ na uzyskanie stabilnego obrazu na ekranie oscyloskopu ma wartość częstotliwości wzorcowej oraz stosunek do niej badanej częstotliwości. Największą stabilność obrazu uzyskać można dla niskich częstotliwości oraz przy stosunku f_x/f_y = 1.



W

Im

Re

T

A

S

t

-A

T/2

Im

Re

S₁,S₂



t

t₀

T



Generator

wzorcowy

f_x

a

b

X

X

Y

Y

1

Układ

formujący

Generator

wzorcowy

Przerzutnik

Bramka

Licznik

Blok

wyświetlaczy

f_x (T_x)

1

1

2

2

a

b

3

4

2

f_x (f_w)

T_w (T_x)

st

1

2

3

4

T_w , (T_x)

N

t

t

t

t

U₁

U₂

U_r

U_s



a

b

A

X₀

B

Y₀

X

Y

Układ

formujący

Układ

formujący

Układ

sterowania

bramką

Bramka

Generator

wzorcowy

Licznik

Wyświetlacz

U₁(t)

U₂(t)

U₁

U₂

---