Przykładowy zestaw na zaliczenie II części ćwiczeń i wykładu z algebry

Część A.

1. Jeżeli
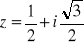
   , to

a)
, b)
, c)
.

2. Macierz
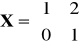
   spełnia równanie
   a)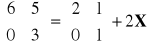
   , b)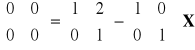
   , c)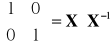
   .

3. Proste
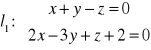
   oraz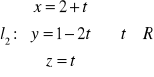
   
   a) są równoległe, b) przecinają się, c) są skośne.

4. Dane są wektory
   ,
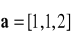
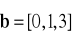
   oraz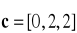
   . Wtedy iloczyn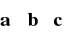
   wynosi
   a)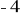
   , b)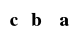
   , c)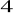
   .

5. Płaszczyzna o równaniu
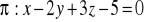
   jest
   a) równoległa do prostej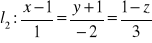
   ,
   b) prostopadła do prostej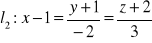
   ,
   c) równoległa do prostej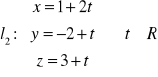
   .

6. Przekształceniem liniowym jest przekształcenie dane wzorem
   a)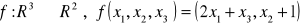
   ,
   b)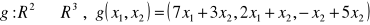
   ,
   c)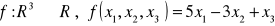
   .

7. Prawdziwe jest zdanie:
   a) Jeżeli wektory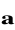
   ,
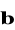
   oraz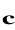
   są wektorami własnymi pewnej macierzy, to są liniowo zależne,
   b) Każda macierz kwadratowa spełnia swoje równanie charakterystyczne.
   c) Każdą macierz kwadratową można diagonalizować.

Część B.

1. Punkty
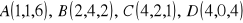
   są wierzchołkami czworościanu.
   a) oblicz objętość czworościanu,
   b) oblicz kosinus kąta pomiędzy wektorami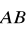
   i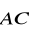
   ; czy ten kąt jest prosty?.

2. Przekształcenie
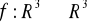
   przestrzeni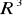
   w siebie dane jest wzorem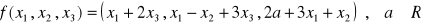
   
   a) dla jakiej wartości parametru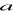
   jest to przekształcenie liniowe?
   b) dla wyznaczonej w punkcie a) wartości parametru napisz macierz przekształcenia liniowego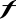
   ,
   c) napisz macierz charakterystyczną, równanie charakterystyczne i wyznacz wartości własne tego przekształcenia,
   d) określ krotność znalezionych wartości własnych i wyznacz odpowiadające im wektory własne.

Uwaga!

W części B mogą być rownież zadania dotyczące układów rownań.

---