Cel ćwiczenia:

Celem ćwiczenia jest wyznaczenie prędkości pocisku za pomocą wahadła balistycznego skrętnego.

Wstęp teoretyczny.

Wahadło balistyczne skrętne stanowi masywne ciało o znacznym i regulowanym momencie bezwładności. Przytwierdzone jest do sprężystego drutu.

Pocisk wystrzelony z odpowiedniego urządzenia trafia w miseczkę A wbijając się w nią. Powoduje to odchylenie wahadła od położenia równowagi. Energia kinetyczna wahadła stopniowo przechodzi w energię potencjalną sprężyście skręconego drutu. Gdy energia potencjalna związana z siłami sprężystości osiągnie maksimum, zaczyna się proces odwrotny: energia potencjalna przechodzi w energię kinetyczną. W sposób ten wahadło zaczyna wykonywać drgania wokół osi przechodzącej przez skręcany drut. Pomiar odpowiednich parametrów tego drgania pozwala na określenie prędkości pocisku.

Korzystając z tego, iż zderzenie wahadła z pociskiem jest całkowicie niesprężyste, można napisać równanie zachowania momentu pędu:

gdzie:

m - masa pocisku

v - prędkość pocisku,

r - odległość wbitego pocisku od osi obrotu,

ω - prędkość kątowa wahadła,

I - moment bezwładności wahadła.

Odkształcenie jakiemu podlega drut wahadła ma charakter sprężysty, zatem zgodnie z prawem Hooke`a moment sił sprężystych M jest proporcjonalny do kąta skręcenia wahadła:

M = -kϕ

Gdzie:

k - sztywność skrętna drutu:

l - długość drutu,

d - średnica drutu,

G - moduł sprężystości

Maksymalna energia skręcanego drutu jest równa:

Szukaną prędkość pocisku obliczymy korzystając z zależności:

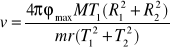
gdzie:

v - szukana prędkość pocisku,

ϕ_max - maksymalny kąt wychylenia wahadła po zderzeniu z pociskiem,

M - masa ciężarka,

m - masa pocisku,

r - odległość osi obrotu wahadła od środka pocisku wbitego w plastelinę,

R₁ - odległość osi obrotu od środka ciężarka, gdy jest on najbliżej miseczek z plasteliną

R₂ - odległość osi obrotu od środka ciężarka, gdy jest on najbliżej osi obrotu,

T₁ - okres drgań dla R₁,

T₂ - okres drgań dla R₂,

Obliczenia.

Wyznaczamy prędkość pocisku v ze wzoru:

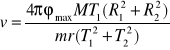
Dane:

M=200 [g] =0,2 [kg]

m = 25 [g] = 0,0025 [kg]

r = 0,12 [m]

R₁ = 0,09 [m]

R₂ = 0,02 [m]

ϕ_max = 25 [°] = 0,436 [rad]

T₁ = 2,29 [s]

T₂=1,35 [s]

Otrzymujemy prędkość pocisku równą:

V = 22,64 [m/s]

Prędkość średnia ruchu pocisku w plastelinie wynosi:

Vśr = ½ V = 11,32 [m/s]

Czas trwania:

t = 1,77*10^-3 [s] = 1,77 [ms]