STATYSTYKA MATEMATYCZNA II ROK WGGIOŚ (2005/2006)

Termin Ia: 31.01.2006 8.30-10.00

Zad. 1 (2pkt)

W wielu sytuacjach można przyjąć, że czas X bezawaryjnej pracy urządzenia jest zmienną losową o gęstości:

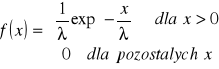
Niech λ=10. a) Obliczyć prawdopodobieństwo Pr(5 ≤ X ≤ 10)

b) Wyznaczyć dystrybuantę zmiennej losowej X

Zad. 2 (2pkt.)

Dla 121 próbek dolomitowych pochodzących z pewnego rejonu wykonano pomiary przewodności elektrycznej. Uzyskano średnią przewodność równą 5400Ωm, a wariancję z próby równą 6.25×10⁶(Ωm)². Wyznaczyć 99% przedział ufności dla wartości oczekiwanej przewodności elektrycznej z tego rejonu.

Zad. 3 (2pkt.)

Dane obserwacje dwóch zmiennych losowych o rozkładach normalnych

x: 2.61 2.30 1.47 3.78 4.29 2.17 5.81 0.49

y: 5.23 3.64 5.04 4.51 5.71 4.03 4.65

Zweryfikować hipotezę o równości wartości oczekiwanych zmiennych X i Y na poziomie istotności 5% i 1%.

Zad. 4 (1.5pkt)

Zdefiniować kowariancję oraz podać twierdzenie o kowariancji i odwrotne twierdzenia o kowariancji. Do czego się te twierdzenia wykorzystuje? (odpowiedź na pytanie w 1 zdaniu!)

Zad. 5 (1.5pkt.)

Dana 10-cio elementowa próba

x: 0.34 0.90 3.48 2.30 3.35 3.11 0.05 3.39 1.81 4.2

pochodząca z populacji o rozkładzie gamma z dystrybuantą

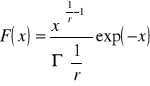
Estymować parametr r metodą momentów jeśli wiadomo, że dla tego rozkładu var(x)=1/r.

Zad. 6 (1pkt)

Dla próby: 2 5 3 2 -1 2 4 3 0 -1

Wyznaczyć medianę i naszkicować histogram skumulowany.

STATYSTYKA EGZAMIN

Termin Ib, 7.02.2006 GRUPA A

1. Do egzaminu z przedmiotu Statystyka ma przystąpić 120 studentów roku II WGGiOŚ. W terminie Ia do egzaminu przystąpiło 24 studentów. Z grupy tej zdało 20 studentów.

1. Przyjmując, że grupa studentów przystępujących do egzaminu w terminie Ia jest reprezentatywną prostą próba losową wszystkich egzaminowanych 120 studentów (w rzeczywistości tak nie jest) wyznaczyć 95% przedział ufności dla proporcji zdanych egzaminów.

2. Uzasadnić w 2-3 zdaniach dlaczego grupa studentów przystępujących do egzaminu w terminie Ia nie jest reprezentatywną prostą próba losową.

(2 pkt)

2. W celu zbadania zróżnicowania poziomu hałasu w różnych miastach Polski wykonano po 4 pomiary poziomu hałasu na rynku w Myślenicach, Krakowie, Warszawie i Tarnowie. Następnie do rozwiązaniu problemu zastosowano analizę wariancji.

1. Jaka hipoteza zerowa była weryfikowana?

2. Sprawozdanie z przeprowadzonych analiz wpadło do wody, wskutek czego jego istotna część - tabela analizy wariancji, uległa zatarciu. Uzupełnij zaznaczone pytajnikami, zatarte miejsca w tabeli.

Rodzaj wariancji	Suma kwadratów	Liczba stopni swobody	Średni kwadrat	Stosunek F
Pomiędzy klasami EFF	13.76	?	?	?
Wewnątrz klas ERR	?	?	?
Całkowita TOT	27.02	?

3. Zweryfikuj hipotezę zerową na poziomie istotności 0.05 i 0.01. Podaj słowną interpretację (w 1 zdaniu!) wyniku interpretacji na każdym poziomie.

(2.5 pkt)

3. Zmienna losowa X ma wartość oczekiwaną E[X]=2 i standardowe odchylenie σ(x)=2.

1. Wyznaczyć wartość oczekiwaną i wariancję zmiennej losowej U = -3X + 1

2. Wyznaczyć kowariancję cov(X,U)

3. Czy zmienne X , U są zależne?

(2 pkt)

4. Zdefiniuj dystrybuantę dwuwymiarowej ciągłej zmiennej losowej
oraz funkcję gęstości rozkładu brzegowego ze względu na zmienną Y

(1 pkt)

5. Wykonano obserwację pewnej zmiennej losowej otrzymując próbę:

1. ; 1.15 ; 0.22 ; 1.74 ; 0.06 ; 0.41 ; 0.96 ; 1.14

Dystrybuanta tej zmiennej ma postać:

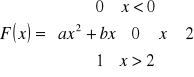
Estymować parametry a i b.

(2.5 pkt)STATYSTYKA EGZAMIN

Termin Ib, 7.02.2006 GRUPA B

1. W pewnych pomiarach uzyskano następujące wyniki par zmiennych X , Y

X	2.9	1.1	0.7	3.7	3.8	0.7	3.1	4.2	3.2
Y	4.5	21.3	11.8	8.6	5.3	13.5	0.8	6.7	12.9

1. Czy z prawdopodobieństwem 95% można stwierdzić, że X , Y są statystycznie zależne? Podać jednozdaniową słowną interpretację analizy.

2. Jaki byłby wniosek na poziomie istotności 0.01 ? Podać jednozdaniową słowną interpretację analizy.

3. Jakie założenia muszą spełniać zmienne X , Y by można było rozwiązać poprawnie a) i b)?

(2.5 pkt)

2. W wyniku pewnego eksperymentu otrzymano średnią arytmetyczną pomiarów
i standardowe odchylenie z próby s_x=1.12. Jak liczna minimalnie musiała by być próba by wynik ten świadczył z prawdopodobieństwem 99% iż wartość oczekiwana mierzonej wielkości jest mniejsza od 3.5 ?

Uwaga: Rozważyć przypadek dużej próby.

(2.5 pkt)

3. Dystrybuanta rozkładu prawdopodobieństwa zmiennej losowej X jest:

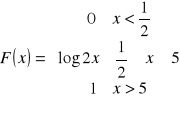
Znaleźć funkcję gęstości prawdopodobieństwa i wartość oczekiwaną zmiennej losowej X.

(2pkt)

4. Zdefiniuj funkcję gęstości dwuwymiarowej ciągłej zmiennej losowej
oraz funkcję gęstości rozkładu warunkowego dla warunku X=x₀.

(1 pkt)

5. Która z funkcji

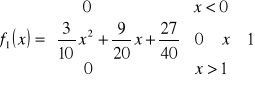
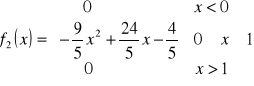
jest, a która nie jest funkcją gęstości prawdopodobieństwa? Odpowiedź uzasadnić.

(2 pkt)

STATYSTYKA EGZAMIN

Termin II, 2.03.2006 GRUPA A

1. Mając funkcję gęstości prawdopodobieństwa zmiennej losowej X:

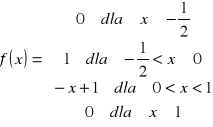
wyznacz dystrybuantę zmiennej X, oblicz E[X] i var(X).

(2.5 pkt)

2. Badając skażenie środowiska wodnego w województwie małopolskim, w dziewięciu losowo wybranych miejscach pobrano próby wody gruntowej i zmierzono w nich między innymi zawartość amoniaku. Na podstawie wyników pomiarów obliczono średnią zawartość amoniaku - 0.383 mg/l oraz odchylenie standardowe - 0.128 mg/l. Zakładając, że badana cecha ma rozkład normalny, na poziomie ufności 99% oszacować przeciętną zawartość amoniaku w wodach województwa małopolskiego.

(2 pkt)

3. Tabela zawiera dane dotyczące opadów (mm) i temperatury (°C) w Krakowie w lipcu w latach 1998-2002:

Opady	68	26	65	136	154
Temperatura	19	19.6	20.6	17.4	19.4

Zakładając, że zmienne mają rozkłady normalne, sprawdzić czy z prawdopodobieństwem 90% można stwierdzić, że istnieje zależność między ilością opadów a temperaturą.

(2.5 pkt)

4. Dana 10-cio elementowa próba

x: 0.34 0.90 3.48 2.30 3.35 3.11 0.05 3.39 1.81 4.2

pochodząca z populacji o rozkładzie gamma z dystrybuantą

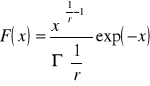
Estymować parametr r metodą momentów jeśli wiadomo, że dla tego rozkładu var(x)=1/r.

(1 pkt)

5. Do podanych poniżej problemów należy dobrać właściwe metody rozwiązywania

Problem 1. Przepisy kraju Bunga-Wonga nakazują by gwarancja na dzidy bojowe pokrywała, na 99%, okres średniego czasu użytkowania dzid. Dla ustalenia długości okresu gwarancyjnego rozdano partię 100 nowych dzid wojownikom plemienia Wa-hima, a następnie rejestrowano czas ich użytkowania do zniszczenia. Jaką metodą statystyczną wyznaczysz długość okresu gwarancyjnego?

Problem 2. Podjęta zostanie próba odpowiedzi na pytania czy aktywność słoneczna ma wpływ na występowanie katastrofalnych zjawisk atmosferycznych. Jako dane pomiarowe zostaną wykorzystane, pochodzące z ostatnich 20 lat: wartości średniej rocznej liczby plam na słońcu oraz łączna liczba huraganów, tornado, tajfunów itp. dla każdego roku. Jaką metodę użyjesz do rozwiązania postawionego problemu?

Problem 3. Planuje się przeprowadzenie badań mających rozstrzygnąć, czy palenie papierosów wpływa na ciśnienie krwi u ludzi młodych. Badania, które przeprowadzone zostaną próbie złożonej z wszystkich studentów płci męskiej WGGiOŚ AGH, polegać będą na pomiarze ciśnienia u studentów palących oraz u studentów niepalących. Jaką metodę użyjesz do analizy zebranych danych dla rozwiązania postawionego problemu?

METODY: A. Testowanie hipotezy o wartości oczekiwanej.

B. Testowanie hipotezy porównawczej dla dwóch wartości oczekiwanych i pomiarów zależnych.

C. Analiza wariancji.

D. Wyznaczanie przedziału ufności dla wartości oczekiwanej.

E. Analiza korelacji

F. Testowanie hipotezy porównawczej dla dwóch wartości oczekiwanych i pomiarów niezależnych.

UWAGA: Wypisać tylko nr problemu - litera metody! Bez żadnej poezji opisowej.

(2 pkt)STATYSTYKA EGZAMIN

Termin II, 2.03.2006 GRUPA B

1. Dla rozkładu o dystrybuancie:

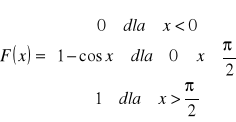
wyznaczyć gęstość prawdopodobieństwa, wartość oczekiwaną i medianę.

(2.5 pkt)

2. Dostawca drewnianych belek twierdzi, że ich średnia wytrzymałość jest równa μ=40kg/cm². Wiadomo z doświadczenia, że wytrzymałość może być uznana za zmienną losową o rozkładzie normalnym. Wybrano losowo 25 belek i zmierzono ich wytrzymałości. Otrzymano średnią wytrzymałość w próbie 39 kg/cm², a odchylenie standardowe 2 kg/cm². Proszę sprawdzić, czy na poziomie istotności 0.1 wynik ten nie przeczy twierdzeniu dostawcy.

(2 pkt)

3. W poniższej tabeli są podane roczne zarobki brutto w regionie środkowoatlantyckim USA, dla następujących grup zawodowych: matematycy i informatycy; biolodzy i pokrewne; fizycy i pokrewne; socjolodzy i pokrewne; inżynierowie. Dane pochodzą z jednego roku i zostały zebrane przez NSF.

	mat.-inf.	fiz.	soc.	biol.	inż.
Region ś-a Zarobki	74, 63, 55	71, 63, 60	60, 55, 55	67, 58, 53	72, 68, 65
Średnie zarobków	64	64.7	56.7	59.3	68.3
SSi	182	64.7	16.7	100.7	24.7

Odpowiedzieć na pytanie, czy z prawdopodobieństwem popełnienia błędu 1% można stwierdzić, że zarobki w wymienionych grupach są różne?

Uwaga: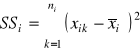

(2.5pkt)

4. Zdefiniować kowariancję oraz podać twierdzenie o kowariancji i odwrotne twierdzenia o kowariancji. Do czego się te twierdzenia wykorzystuje? (odpowiedź na pytanie w 1 zdaniu!)

(1 pkt)

5. Do podanych poniżej problemów należy dobrać właściwe metody rozwiązywania

Problem 1. W problemie tym próbujemy rozstrzygnąć, czy spożyty alkohol wpływa niekorzystnie na czas reakcji kierowcy. Eksperyment przeprowadzono w pewnej grupie kierowców. Najpierw zmierzono ich czasy reakcji na bodziec. Następnie podano im po 100 g wódki. Po 15 minutach od konsumpcji (bez zakąski) zmierzono ich czasy reakcji na ten sam bodziec. Jaką metodą statystyczną użyjesz do opracowania wyników dla rozwiązania problemu?

Problem 2. Polski Związek Narciarski zdecydował się wysłać na olimpiadę w Turynie Kamila Stocha gdyż na podstawie jego skoków treningowych wykonanych w okresie 20.01-5.02 stwierdzono, że przeciętna długość jego skoku na Wielkiej Krokwi w Zakopanem była nie mniejsza niż 120m. Jaką metodą analizy danych posłużył się PZN dla otrzymania tego wyniku?

Problem 3. Postanowiono zbadać, czy przeciętny czas życia świnki morskiej jest zależny od wieku jej właściciela. Wybrano losowo 250 świnek i ich właścicieli. Właścicieli pogrupowano w przedziałach wieku: poniżej 7 lat, 7-10, 11-14, 15-20, powyżej 20 lat. Następnie rejestrowano czas jaki świnkom udało się przeżyć. Jaką metodę użyto do analizy zebranych danych dla rozwiązania postawionego problemu?

METODY: A. Testowanie hipotezy o wartości oczekiwanej.

B. Testowanie hipotezy porównawczej dla dwóch wartości oczekiwanych i pomiarów zależnych.

C. Analiza wariancji.

D. Wyznaczanie przedziału ufności dla wartości oczekiwanej.

E. Analiza korelacji

F. Testowanie hipotezy porównawczej dla dwóch wartości oczekiwanych i pomiarów niezależnych.

UWAGA: Wypisać tylko nr problemu - litera metody! Bez żadnej poezji opisowej.

(2 pkt)

---