Kogut Andrzej Rzeszów, 25-V-1996

Grupa L - 11

Sprawozdanie z laboratorium z fizyki

Ćwiczenie nr 27

1.Prąd sinusoidalnie zmienny, wielkości charakterystyczne, wielkości charakteryzujące wartość średnią, skuteczną, szczytową. Prąd elektryczny jest to zjawisko fizyczne wywołane uporządkowanym ruchem ładunków poprzez badany przekrój poprzeczny danego ośrodka. Prąd zmienny - w funkcji czasu ulega zmianie natężenie lub zwrot płynącego prądu. Prąd przemienny - zmiany te zachodzą okresowo. Prąd sinusoidalnie przemienny - prąd, którego przebieg jest sinusoidalną funkcją czasu.

i(t) = Im sin(t +)

i(t) - wartość chwilowa natężenia prądu

Im - wartość szczytowa natężenia prądu

- pulsacja (częstotliwość kołowa)

- faza początkowa

Wartość skuteczna natężenia prądu przemiennego jest to wartość

liczbowo równa takiej wielkości prądu stałego , który w tym samym

czasie i na tym samym oporze wydzieli taką samą ilość ciepła.

Wartość średnia półokresowa prądu przemiennego jest równa liczbowo takiej wartości prądu stałego , który w tym samym czasie (połowie okresu) przeniesie taki sam ładunek co dany prąd przemienny . Wartość średnia całookresowa prądu przemiennego jest równa zero , dlatego podaje się wartość średnią półokresową, liczy się ją ze wzoru.

2.

A. Indukcyjność w obwodzie prądu zmiennego .

Jeżeli do źródła prądu stałego o napięciu U przyłączymy cewkę o wielu zwojach (idealną R 0 ) to przez taką zwojnicę mógłby płynąć prąd ( teoretycznie ) o bardzo dużym natężeniu ograniczonym tylko opornością wewnętrzną źródła .Jeżeli tę samą cewkę ( pozbawioną oporności czynnej ) przyłączymy do źródła prądu zmiennego to natężenie prądu będzie ograniczone poprzez siłę elektromotoryczną indukcji własnej

eL = - L (di/dt) lub eL = -z (d/dt)

L- współczynnik indukcyjności własnej

- szybkość zmian strumienia

Gdy L > 0 , R=0 , C=0

i = Imsin(t)

spadek napięcia uL= -eL

Jak widać natężenie prądu jest opóźnione o kąt 900 w stosunku do napięcia .

B. Kondensator w obwodzie prądu zmiennego.

Napięcie doprowadzone ze źródła prądu zmiennego do okładzin kondensatora zmienia się sinusoidalnie :

u = Umsin(t)

jak i prąd w kondensatorze

i = dq/dt

dq = Cdu= CUm cos(t)dt

i = CUmcos(t)

cos = sin (+/2)

i = CUmsin (t+/2)

Przepływający przez kondensator prąd zmienny ma natężenie o prze-

biegu sinusoidalnym , które wyprzedza napięcie o kąt 900 .

Szczytowa wartość natężenia prądu wynosi : Im = CUm

C. Rezystor w obwodzie prądu zmiennego.

R > 0, L = 0, C = 0

Wartość natężenia prądu przepływającego przez opornik wyraża się równaniem i =Imsin(t)

Spadek napięcia na oporności czynnej R przy jej niezmiennej

wartości jest wprost proporcjonalny do natężenia przepływającego prądu. Chwilowe napięcie jest największe ( Um ) gdy wartość chwilowa przepływającego prądu jest największa . Napięcie i prąd są zgodne w fazie. Związek między napięciem i prądem chwilowym U = RImsin(t) .

D. Obwód szeregowy RLC

Obwód szeregowy RLC składa się z połączonych ze sobą szeregowo rezystancji, indukcyjności i pojemności. Napięcie chwilowe u = uR +uL + uC.

Wartość skuteczna napięcia doprowadzonego do zacisków układu jest sumą geometryczną uR , u L ,u C .UL i uC są przesunięte w fazie względem uR o +90 i -90 .

Z - impedancja (oporność pozorna )

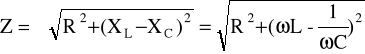
Obwody zasilane prądem zmiennym, zawierające elementy bierne i czynne powodują przesunięcie fazowe pomiędzy prądem a napięciem. Kąt przesunięcia fazowego jest określony poprzez

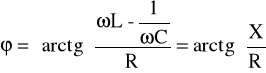
3.

Wykonanie ćwiczenia:

1. Połączenie obwodu wg. schematu:

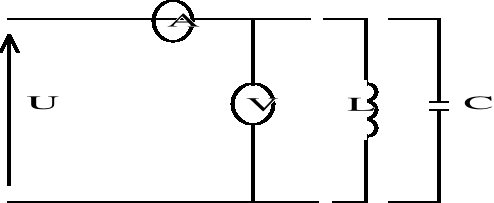
1.a) Przyrządy do wykonania ćwiczenia:

Amperomierz i voltomierz na prąd stały i przemienny, kondensator, cewka.

2. Wyznaczam opór czynny z prawa Ohma (dla prądu stałego)

Tabela pomiarowa dla wyznaczenia oporu czynnego z prawa Ohma (dla prądu stałego)

Lp	U [V]	I [A]	R []
1	2,5	0,13	19,23
2	5	0,26	19,23
3	7,5	0,395	18,98
4	10	0,53	18,86
5	11	0,58	18,95
6	12,5	0,66	19,69

R i R wyznaczone graficznie na załączonym wykresie

R = ctg ; R=20

R = 1.4

3. Wyznaczam oporność pozorną cewki (prąd zmienny)

Tabela pomiarowa dla wyznaczenia oporności pozornej cewki:

Lp	U [V]	I [A]	Z []
1	10	0,23	43,47
2	15	0,34	44,11
3	20	0,47	42,55
4	25	0,57	43,85
5	30	0,7	42,85
6	35	0,79	44,30

Z oraz Z również wyznaczone graficznie na załączonym wykresie

Z = ctg ; Z = 22.7

Z = 0.3

4. Obliczam indukcyjność cewki:

f = 50 Hz.

L = 3067.8H

L obliczam z różniczki zupełnej:

L = 0,2376 H

=0.2376

5. Wymieniam cewkę na kondensator i wyznaczam oporność bierną kondensatora przy zasilaaniu prądem zmiennym:

Tabela pomiarowa:

Lp	U [V]	I [A]	XC[]
1	34	0,1	340
2	48	0,15	320
3	63	0,2	315
4	78	0,25	312
5	84	0,27	311,11
6	94	0,3	313,33

XC oraz XC wyliczam korzystając z metody najmniejszych kwadratów.

XC = 318

6. Oblczam wartość pojemności z zależności:

C = 0,00001 F

Błąd C oblczam z różniczki zupełnej.

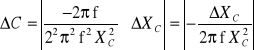
Wnioski:

Na podstawie przeprowadzonych pomiarów i obliczeń wnioskuję, że doświadczenie przebiegło pomyślnie. Zaistniałe błędy mogły wyniknąć "z przyczyn niezależnych" tzn. niestabilne napięcie zasilające, niestała częstotliwość prądu w sieci elektrycznej a także niedokładność pomiarów na miernikach. Na błędy pomiarowe złożyły się następujące czynniki: nieprecyzyjny odczyt ze skali wskazówkowej, błędy sprzętowe, niestabilność układu zasilającego. Pomimo zaistniałych błędów wyniki uzyskane przy pomiarach jak i w późniejszych obliczeniach uważam za zadowalające.

Kogut Andrzej Rzeszów 25-05-96

C 06 - L 11

Laboratorium fizyki

Ćwiczenie nr.51

1. Zasada działania mikroskopu:

Mikroskop składa się z dwóch soczewek skupiających ustawionych w odległości większej niż suma ogniskowych zastosowanych soczewek. Mikroskop posiada bardzo małe pole widzenia .

Pierwsza soczewka (obiektyw) daje obraz rzeczywisty odwrócony i powiększony. Druga soczewka (okular) działa jak lupa i daje obraz urojony , powiększony i prosty.

2. Powietrzny klin interferencyjny.

Jeżeli światło monochromatyczne oświetla nam powierzchnię rozgraniczającą dwa ośrodki to część światła odbija się a część przejdzie dalej . Jeżeli dwie powierzchnie ustawimy w kształt klina to światło padające na nie :

Przy zgodnej fazie dochodzące do płytki to tworzy się jasny prążek

Przy przeciwnej wtedy tworzy się prążek ciemny

tak że widać prążki na przemian ciemne i jasne.

Podobnie dzieje się z soczewkami . Soczewka jako powierzchnia p1 natomiast szkło jako powierzchnia p2 z tą tylko różnicą że prążki będą kuliste i ich gęstość będzie wzrastała w takt krzywizny powierzchni soczewki.

3. Układ pomiarowy :

Jest to mikroskop , na którego stoliku umieszczamy płaską płytkę P ; mierzoną soczewkę L₀

Są one oświetlone poprzez obiektyw mikroskopu równoległą wiązką światła monochromatycznego , za pomocą soczewki i półprzepuszczalnego zwierciadła Z umieszczonego nad obiektywem mikroskopu . Okular ma podziałkę za pomocą pomocą której ustawia się wybrany obraz prążka . Ustawienie i pomiar u_możliwia przesuwany stolik mikroskopu , którego przesuw jest mierzony za pomocą czujnika zegarowego . Mała wskazówka czujnika wskazuje milimetry a duża setne części milimetra.

4. pomiar krzywizny soczewki:

a) Powierzchnię soczewki i płytki płaskiej przemyć spirytusem i przetrzeć do sucha czystą flanelą .

b) Położyć badaną soczewkę płasko-wypukłą na płytkę szklaną i umieścić na stoliku mikroskopu . Stolik powinien być ustawiony w położeniu środkowym . Należy ustawić soczewkę tak aby środkowy (zerowy ) prążek wypadł na działkę oznaczoną cyfrą 5 podziałki okularu mikroskopu .

c) Dokonać pomiarów średnicy wybranych ciemnych prążków o możliwie dużych średnicach;

-podziałkę oznaczoną cyfrą 5 przyjmujemy jako pkt. 0 .

-następnie przesuwając stolik na k-ty prążek odczytujemy wskazanie.

-podobnie postępujemy tylko stolik przesuwamy w przeciwną stronę.

Kogut Andrzej Rzeszów 16-05-96

C 06 L11

Laboratorium fizyki

Ćwiczenie nr 10

1. Zagadnienia do samodzielnego opracowania:

a) Fale mechaniczne

Z ruchem falowym spotykamy się niemal we wszystkich działach fizyki. Mamy fale mechaniczne , fale elektromagnetyczne , a nawet fale materii. Fale mechaniczne czyli zjawiska ruchu falowego w ośrodkach sprężystych są najłatwiej dostrzegalne . Wytrącanie zespołu cząsteczek takiego ośrodka z położenia równowagi powoduje ich drganie wokół tego położenia, przy czym dzięki dzięki właściwościom sprężystym ośrodka, zaburzenie przenosi się z jednej jego warstwy na następną , wprawiając ją w ruch drgający o określonej częstotliwości . przykładem fali mechanicznej jest fala rozchodząca się kołowo na powierzchni wody po wrzuceniu kamienia.

b) Rodzaje fal:

W zależności od kierunku drgań cząsteczek ośrodka w stosunku do kierunku rozchodzenia się fali rozróżnia się fale podłużne i poprzeczne. Fala poprzeczna występuje wtedy gdy cząsteczki ośrodka sprężystego drgają prostopadle do kierunku rozchodzenia się fali. Natomiast fala podłużna występuje wtedy gdy cząsteczki ośrodka drgają wzdłuż kierunku rozchodzenia się fali. Odległość między dwiema najbliższymi cząsteczkami ośrodka drgającego mającymi jednakowe fazy nazywamy długością fali l .

Falę określamy następującymi równaniami:

c) Superpozycja fal:

Jeżeli przez ośrodek sprężysty przechodzi równocześnie kilka fal rozchodzących się z różnych źródeł drgań, to każda cząsteczka ośrodka uczestniczy w kilku nakładających się wzajemnie ruchach drgających. Zasada superpozycji mówi nam , że wychylenie jakiego doznaje każda cząsteczka ośrodka jest sumą wektorową wychyleń , jakich doznałaby przy rozchodzeniu się każdej fali z osobna .

Drgania cząsteczki mogą się osłabiać lub wzmacniać , w zależności od tego czy są wynikiem nakładania się fal o fazach zgodnych , czy też przeciwnych. Zjawisko to nosi nazwę interferencji fal.

d) Fale stojące:

Szczególnym przypadkiem interferencji jest powstawanie fali stojącej będącej wynikiem nakładania się dwóch fal o jednakowych amplitudach , częstotliwościach i prędkościach rozchodzących ie ośrodku srężystym w przeciwnych kierunkach.

2. Dwa ciągi fal o równych amplitudach lecz nieco różnych częstotliwościach rozchodzące się w tym saym ośrodku dając dudnienia. Wyraźne zaburzenie powodowane przez jedną falę w dowolnym punkcie ośrodka opisuje równanie:

y1=y0cos(w1t-kx+f1)

y2=y0cos(w2t-kx+f2)

3. Przebieg ćwiczenia :

a) ustawić widełki stroikowe w ten sposób , by pudła rezonansowe były skierowane otworami ku sobie .

b) nałożyć pierścień i ustawić go w położeniu wskazanym przez prowadzącego zajęcia . Częstotliwość drgań widełek z pierścieniem przyjąć f1 Uderzając młoteczkiem w obie pary widełek wywołać dudnienie.

c) zmierzyć czas t1 dziesięciu kolejnych wzmocnień dźwięku Pomiary powtórzyć kilka razy . Obliczyć czas dudnienia Td2 .

d) Obliczyć częstotliwość drgań widełek stroikowych z pierścieniem .

Tabela pomiarowa:

Lp.	f1	y	T1	T2	Td1	Td2	fd	fa * Df2
1	435	góra	3,67	4,48	0,27	0,21
2			3,23	3,81	0,31	0,26
3			3,24	4,42	0,31	0,23
4			3,27	3,84	0,31	0,26
5		3/4 wys.	3,09	3,87	0,32	0,26
6			7,51	7,14	0,13	0,14
7			7,84	7,41	0,12	0,13
8			8	7,11	0,12	0,14
9			7,72	7,39	0,12	0,13
10			7,84	7,06	0,12	0,14

Kogut Andrzej Rzeszów dn.25-05-96

C 06 - L11

Laboratorium fizyki

Ćwiczenie nr. 45

1. Zagadnienia do samodzielnego opracowania:

- ruch falowy, rodzaje fal.

Fala jest to przemieszczające się odchylenie ze stanu równowagi punktu (atomu, cząsteczki ) który następnie pociąga za sobą odchylenie dalszych punktów.

Rozróżniamy następujące rodzaje fal:

ze względu na kształt czoła :sferyczna płaska.

ze względu na sposób przemieszczania : podłużna , poprzeczna.

- Polaryzacja fali

Polaryzacja jest to uporządkowany ruch ośrodka fali w stosunku do kierunku rozchodzenia się fali.

Rozróżniamy polaryzację liniową , równoległą , poprzeczną.

- polaryzacja światła przy odbiciu i załamaniu .

Światło padające na przezroczystą płytkę szklaną , częściowo zostaje odbite , właśnie ta odbita wiązka jest spolaryzowana częściowo (liniowo) . Taką polaryzację nazywamy polaryzacją przez odbicie .

Polaryzacja światła przy załamaniu :

Są kryształy podwójnie łamiące w których światło przechodzące przez nie zostaje rozbite na dwie wiązki :

promień zwyczajny oraz promień nadzwyczajny . Oba te promienie są spolaryzowane w płaszczyznach do siebie prostopadłych.

-wielkości fotometryczne:

Spektralna gęstość promieniowania Bl W/m2

Gęstość promieniowania B= Bldl W/m2

Natężenie źrudła światła I= BdS W/sr

Moc promieniowania f= Ido W

Oświetlenie E=f/s W/m2

2. Wykonanie ćwiczenia.

Badanie stanu spolaryzowania wiązki światła odbywać się może za pomocą układu składającego się z dwóch ośrodków polaryzujących zwanych polaryzatorami i analizatorem. Po przejściu przez polaryzator światło jest liniowo spolaryzowane . Kolejno , światło przechodzące przez analizator jest ponownie polaryzowane liniowo. Konsekwencją takiego stanu rzeczy , spolaryzowanej wiązki świetlnej jest zmiana jego natężenia po przejściu przez układ polaryzator - analizator. Zależność tą opisuje prawo Malusa.

I = I0 cos2 a

lp.	aI	I	Da	DI
-	[]	[lx] 0.1	[]	[lx]
1	90	8
2	40	38
3	60	22
4	0	53
5	30	44
6	120	27
7	150	47
8	100	11
9	180	52
10	200	48
11	220	37
12	45	53	0.5	1.5
13	270	7
14	330	46
15	350	52
16	360	52
17	20	47
18	75	10
19	170	51
20	250	12
21	300	25
22	345	51
23	130	34
24	10	50

Wnioski:_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Kogut Andrzej Rzeszów 25-05-96

C 06 - L 11

Laboratorium fizyki

Ćwiczenie nr 46

1. Zagadnienia do samodzielnego opracowania :

- ruch falowy , rodzaje fal

- Ruch falowy powstaje poprzez wychylenie ze stanu równowagi cząsteczki , która następnie powoduje drgania cząsteczek w jej sąsiedztwie.

Rozróżniamy fale o przebiegu sinusoidalnym , prostokątnym itd. Najbardziej rozpowszechnioną jest falą jest fala o przebiegu sinusoidalnym .

Fale dzielimy również ze względu na sposób rozchodzenia , dzielimy je na:

podłużną poprzeczną

Jak również na kształt czoła fali:

płaską , sferyczną.

-Dyfrakcja , interferencja , siatki dyfrakcyjne .

Dyfrakcją nazywamy ugięcie się fali na krawędziach , szczelinach .

Interferencją nazywamy nakładanie się fal , w której występuje :

nakładanie fal o zgodnych fazach tym samym następuje wzmocnienie dodawanie faz (wzmocnienie)

nakładanie fal o przeciwnych fazach co powoduje nakładanie faz różnych a tym samym zanik fazy.

Siatką dyfrakcyjną nazywamy dużą liczbę płasko-równoległych szczelin oddzielonych równymi nieprzezroczystymi przerwami.

Siatkę dyfrakcyjną uzyskuje się np. przez zarysowanie równoległymi rowkami płasko-równoległej płytki szklanej .

Powierzchnie nie zarysowane tworzą szczeliny , matowe zaś rowki nie przepuszczają światła , odległość d równa jest sumie szerokości szczeliny i nieprzezroczystej przerwy.

-wielkości fotometryczne:

Spektralna gęstość promieniowania Bl W/m2

Gęstość promieniowania B= Bldl W/m2

Natężenie źródła światła I= BdS W/sr

Moc promieniowania f= Ido W

Oświetlenie E=f/s W/m2

2. Cel ćwiczenia .

Celem niniejszego ćwiczenia jest wyznaczenie stałej siatki dyfrakcyjnej. Zakładamy że na siatkę dyfrakcyjną pada fala płaska światła monochromatycznego , która po przejście przez siatkę ulega ugięciu . Ugięte fale przechodzące z sąsiednich szczelin nakładają się dając na ekranie maxima w przypadku d=Kl

lp.	l	x	Dx	y	Dy	sinf	d+_Dd
-	nm	cm	cm	cm	cm		nm
1	632,8	2,2	0,05	19	0,9	0,127	5547,96
2		1,9		17		0,121	5739,7
3		1,3		10		0,129	4937,26
4		1,7		15		0,117	5657,91
5		0,9		7		0,108	4986,89
6		1,4		12		0,099	5493,78
7		1,7		14		0,113	5285,87
8		1,1		9		0,113	5243,73
9		1,3		11		0,111	5422,91
10		1,8		16		0,115	5700,95
11		1,6		14		0,115	5609,77

D=dsinf

l=d
*d

sinf=

5054,96

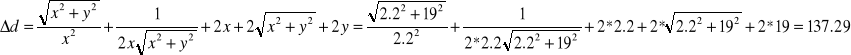
(d+Dd)śr=5420,61

Wnioski:

Przy długości fali świetlnej l=632nm stała siatki dyfrakcyjnej wynosi d=5054.96

Błędy wynikające z pomiarów spowodowane są dużą niedokładnością przyrządu

Kogut Andrzej Rzeszów 22.04.1996

I ED - L 11

Laboratorium fizyki

Ćwiczenie nr 24

Wyznaczanie ładunku właściwego e/m elektronów .

1. Zachowanie się ładunków elektrycznych w polu elektrycznym i magnetycznym .

2. Lampa Browna .

Ad. 1

Na wiązkę elektronów przechodzących przez obszar , w którym istnieje pole magnetyczne o indukcji B działa siła :

I . Ruch naładowanej cząstki odbywa się wzdłuż linii indukcji pola magnetycznego , przy takim ruchu cząstki kąt zawarty między wektorem jej prędkości i wektorem indukcji B równa się 0 lub , w wyniku czego siła Lorentza jest równa 0 ( na cząstkę nie działa pole magn . ) .

II . Cząstka porusza się prostopadle do linii indukcji magn . :
, siła Lorentza FL = q * v * B , oraz skierowana jest prostopadle do wektorów v i B .

Cząstka porusza się w płaszczyźnie do wektora B , a FL pełni rolę siły dośrodkowej :

III. Ruch cząstki w polu magn . gdy jej wektor prędkości v skierowany jest pod dowolnym kątem do wektora indukcji pola B .

Rozkładamy wektor v na dwie składowe :

-
- składowa równoległa do B

-
- składowa prostopadła do B

Prędkość
nie ulega zmianie w polu magn .Cząstka posiada niezerową składową w wyniku czego powinna ona obiegać po okręgu , którego płaszczyzna jest prostopadła do B , a promień

Cząstka uczestniczy w dwóch ruchach jednocześnie w wyniku czego cząstka porusza się po linii śrubowej , której oś pokrywa się z linią indukcji pola magn. , a skok wynosi

Ad .2

Przyrządem służącym do wyznaczanie ładunku właściwego elektronów jest lampa Browna . Elektrony wybiegające na skutek termoemisji z katody lampy są poddawane działaniy pola elektrycznego pomiędzy katodą a anodą lampy .

Skutkiem działania pola elektrycznego jest wzrost prędkości elektronów od wart .

v=0 (przy katodzie) do v = v (tuż przy anodzie) , czyli en . kinetyczna e po dojściu do anody wynosi :

zgodnie ze wzorem
:

Elektron biegnący z taką prędkością lub wiązka uderza w ekran lampy powodując pojawienie się plamki świetlnej . Plamka zostanie przesunięta o wart. y , gdy wiązka elektronów przed uderzeniem w ekran przejdzie przez jednorodne pole magn .

Natężenie pola magn . wewnątrz cewek jest równe :

R - promień cewki

i - nat. prądu płynącego przez cewki

n - ilość zwojów w cewce

Znając wart. sił działających na wiązkę elektronów przechodzącą przez pole magn.

otrzymamy :

Wiedząc , że dla próżni B = 0 H , 0 = oraz wstawiając wart. v możemy napisać :

stąd :

promień krzywizny ruchu elektronów wiąże się z wielkością odchylenia plamki y na ekranie lampy oraz z odl . l cewek odchylających od ekranu zależnością :

ostatecznie otrzymamy :

po podstawieniu za R i n wart. mamy :

III . Wykonanie ćwiczenia .

Przyrządy : lampa oscylograficzna z układem cewek , miliamperomierz , zasilacz regulowany .

1. Po włączeniu i pojawieniu się plamki na ekranie lampy ustawić plamkę w położeniu zerowym na skali oraz pokrętłami ustawić punktowy rozmiar plamki i jasność (ostry , wyraźny punkt ) .

2. Połączyć obwód wg schematu .

3. Odczytywać wychylenie plamki na skali y przy kolejnych nat . prądu płynącego przez cewki : 10 , 20 , 30 , 40 mA .

4. Zmienić kierunek prądu w cewkach na przeciwny i ponownie odczytać wychylenia przy tych samych nat. prądu .

5. Tabelka pomiarów .

Lp.	U [V]	l [m]	i1 [mA]	y1 [cm]	i2 [mA]	y2 [cm]	e/m (1)	e/m (2)	e/msr+e/m
1.	1500	0.3
2.	1500	0.3
3.	1500	0.3
4.	1500	0.3
5.	1500	0.3
6.	1500	0.3
7.	1500	0.3
8.	1500	0.3
9.	1500	0.3
10.	1500	0.3
11.	1500	0.3
12.	1500	0.3
13.	1500	0.3
14.	1500	0.3
15.	1500	0.3

Kogut Andrzej Rzeszów 18.05.96

grupa 11

Laboratorium fizyki

ĆWICZENIE 9

Sprawdzanie równania ruchu obrotowego brył

1.Wielkości charakteryzujące ruch obrotowy można przedstawić w analogiczny sposób jak wielkości charakterystyczne dla ruchu postępowego i tak :

chwilowa prędkość liniowa chwilowa prędkość kątowa

przyśpieszenie chwilowe dla obu ruchów ma postać :

Droga w ruchu postępowym i obrotowym :

znak + dla ruchu przyśpieszonego,

- dla ruchu opóźnionego.

Zasady dynamiki dla ruchu:

a) postępowego

Jeżeli ciało o masie m porusza się z przyśpieszeniem
, to na ciało działa siła

b) obrotowego

Moment bezwładności I ciała względem osi O określamy następująco

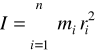
Jeżeli ciało o momencie bezwładności I porusza się z przyśpieszeniem kątowym
, to na ciało działa moment siły

Część teoretyczna ćwiczenia.

Równanie ruchu obrotowego bryły ma postać
(1)

gdzie:
- moment siły,

I - moment bezwładności,

- przyśpieszenie kątowe.

Równanie dynamiki dla ciała o masie m przedstawia zależność

(2a)

gdzie:
- przyśpieszenie z jakim porusza się ciężarek o masie m,

- przyśpieszenie ziemskie

- siła naciągu nici.

W omawianym przypadku moment siły wyraża się wzorem:

(2b)

gdzie: r - ramię siły, czyli promień tej części walca na której nawija się nić.

Obliczamy
z równania (2a) i podstawiamy do równania (2b), co daje

(3)

Moment bezwładności układu I równy jest sumie momentów stałej części
i walców
.

Moment bezwładności walców I , zgodnie z prawem Steinera wynosi:

gdzie: I - moment bezwładności walca W względem osi przechodzącej przez środek ciężkości i równoległej do osi obrotu przyrządu,

M - masa walca W,

R - odległość środka ciężkości walca od osi obrotu.

Ze względów praktycznych odległość R zastępujemy odległością przeciwległych walców d (d = 2R).

Zatem całkowity moment bezwładności wyraża się wzorem:

(3a)

Pierwsze dwa wyrazy po prawej stronie tego wyrażenia są wielkościami stałymi. Wprowadzamy więc oznaczenie:
i otrzymujemy:

(3b)

Łącząc równanie (1), (3), (3b) otrzymujemy

(4)

Ze względu na to, że wektory
i
są prostopadle do osi obrotu, a wektor
jest do niej równoległy, w równaniu (4), możemy zaniedbać znaki wektorów.

Pamiętając że,
oraz
,

gdzie:
- wysokość spadania ciężarka o masie m,

t - czas spadania

i wykonując ponadto przekształcenia algebraiczne otrzymujemy:

(5)

W układzie współrzędnych, w którym na osi y odkładamy
, a na osi x,
, równanie (5) jest równaniem prostej typu:

(6)

(7)

daje wartość rzędnej w punkcie, w którym prosta przecina oś rzędnych. Stromość otrzymanej prostej wyraża się poprzez:

(8)

Prostoliniowy przebieg zależności
jest dowodem słuszności równania ruchu obrotowego bryły. Zależność tę należy wyznaczyć doświadczalnie.

Wykonanie ćwiczenia.

W niniejszym ćwiczeniu posługujemy się wahadłem Oberbecka. Walec metalowy może obracać się wokół osi prostopadłej do osi przyrządu. Z walcem tym połączone są cztery pręty stalowe na których nasadzone są walce. Położenie tych walców na prętach można dowolnie zmieniać. Na walcu osadzone są szpulki na które nawija się nić. Na końcu nici przerzuconej przez bloczek zawiesza się ciężarki.

Tabela pomiarowa:

Ponieważ :

z wykresu możemy odczytać te wartości, a mając dane A i B możemy wyznaczyć M i Ic.

A =42,1 [s2/m2]

B =1.1 [s2]

Wyniki :

Ic = 4,54752 [gm2]

I = Ic + Md2

I

Wnioski :

Masa M która została wyznaczona z wykresu tylko nieznacznie odbiega od masy wyznaczonej doświadczalnie (tzn. masy wybitej na ciężarku). Różnica ta wynikła zapewne dla tego gdyż przy wykonywaniu ćwiczenia popełnione zostały błędy związane z pomiarem czasu i długości.

Poprzez oszacowanie nachylenia prostej można wyznaczyć wartość współczynnika kierunkowego tej prostej. Mając tą wartość można wyznaczyć masę M walca. Prostoliniowy przebieg zależności t2=f(d2) świadczy o słuszności równania ruchu obrotowego.

M	m	r	d	d2	t	t2	I	Ic
193	215	4,5	48	2304	7,174	51,4662
					6,925	47,9556
					6,589	43,4149
					6,535	42,7062
			32	1024	6,247	39,025
					4,645	21,576
					4,378	19,1668
					4,201	17,6484
					4,5	20,25
			18	324	4,518	20,4123
					3,112	9,6845
					3,27	10,6929
					3,231	10,4393
					3,22	10,3684
					3,245	10,53

Kogut Andrzej Rzeszów 16-05-96

C 06 L11

Laboratorium fizyki

Ćwiczenie nr 10

1. Zagadnienia do samodzielnego opracowania:

a) Fale mechaniczne

Z ruchem falowym spotykamy się niemal we wszystkich działach fizyki. Mamy fale mechaniczne , fale elektromagnetyczne , a nawet fale materii. Fale mechaniczne czyli zjawiska ruchu falowego w ośrodkach sprężystych są najłatwiej dostrzegalne . Wytrącanie zespołu cząsteczek takiego ośrodka z położenia równowagi powoduje ich drganie wokół tego położenia, przy czym dzięki właściwościom sprężystym ośrodka, zaburzenie przenosi się z jednej jego warstwy na następną , wprawiając ją w ruch drgający o określonej częstotliwości . przykładem fali mechanicznej jest fala rozchodząca się kołowo na powierzchni wody po wrzuceniu kamienia.

b) Rodzaje fal:

W zależności od kierunku drgań cząsteczek ośrodka w stosunku do kierunku rozchodzenia się fali rozróżnia się fale podłużne i poprzeczne. Fala poprzeczna występuje wtedy gdy cząsteczki ośrodka sprężystego drgają prostopadle do kierunku rozchodzenia się fali. Natomiast fala podłużna występuje wtedy gdy cząsteczki ośrodka drgają wzdłuż kierunku rozchodzenia się fali. Odległość między dwiema najbliższymi cząsteczkami ośrodka drgającego mającymi jednakowe fazy nazywamy długością fali l .

Falę określamy następującymi równaniami:

c) Superpozycja fal:

Jeżeli przez ośrodek sprężysty przechodzi równocześnie kilka fal rozchodzących się z różnych źródeł drgań, to każda cząsteczka ośrodka uczestniczy w kilku nakładających się wzajemnie ruchach drgających. Zasada superpozycji mówi nam , że wychylenie jakiego doznaje każda cząsteczka ośrodka jest sumą wektorową wychyleń , jakich doznałaby przy rozchodzeniu się każdej fali z osobna .

Drgania cząsteczki mogą się osłabiać lub wzmacniać , w zależności od tego czy są wynikiem nakładania się fal o fazach zgodnych , czy też przeciwnych. Zjawisko to nosi nazwę interferencji fal.

d) Fale stojące:

Szczególnym przypadkiem interferencji jest powstawanie fali stojącej będącej wynikiem nakładania się dwóch fal o jednakowych amplitudach , częstotliwościach i prędkościach rozchodzących się ośrodku sprężystym w przeciwnych kierunkach.

2. Dwa ciągi fal o równych amplitudach lecz nieco różnych częstotliwościach rozchodzące się w tym samym ośrodku dając dudnienia. Wyraźne zaburzenie powodowane przez jedną falę w dowolnym punkcie ośrodka opisuje równanie:

y1=y0cos(w1t-kx+f1)

y2=y0cos(w2t-kx+f2)

3. Przebieg ćwiczenia :

a) ustawić widełki stroikowe w ten sposób , by pudła rezonansowe były skierowane otworami ku sobie .

b) nałożyć pierścień i ustawić go w położeniu wskazanym przez prowadzącego zajęcia . Częstotliwość drgań widełek z pierścieniem przyjąć f1 Uderzając młoteczkiem w obie pary widełek wywołać dudnienie.

c) zmierzyć czas t1 dziesięciu kolejnych wzmocnień dźwięku Pomiary powtórzyć kilka razy . Obliczyć czas dudnienia Td2 .

d) Obliczyć częstotliwość drgań widełek stroikowych z pierścieniem .

Tabela pomiarowa:

Lp.	f1	y	T1	T2	Td1	Td2	fd	fa * Df2
1	435	góra	3,67	4,48	0,27	0,21
2			3,23	3,81	0,31	0,26
3			3,24	4,42	0,31	0,23
4			3,27	3,84	0,31	0,26
5		3/4 wys.	3,09	3,87	0,32	0,26
6			7,51	7,14	0,13	0,14
7			7,84	7,41	0,12	0,13
8			8	7,11	0,12	0,14
9			7,72	7,39	0,12	0,13
10			7,84	7,06	0,12	0,14

---