Systemy funkcjonalne pełne.
Zbiór operacji takich, że każda funkcja przełączająca może być przedstawiona za pomocą argumentów i stałych 0 i 1 oraz tych operacji nosi nazwę SFP.
Funkcje logiczne (+,*,-) tworzą tzw. podstawowy system funkcjonalny pełny.
Podstawowy SFP jest wykorzystywany do sprawdzania czy jakiś zbór operacji jest SFP. Przyjmuje się, że jeśli przy użyciu badanego zbioru operacji można przedstawić np. (+,*,-) to ten zbiór operacji tworzy SFP.
Szczególną rolę w zbiorach operacji tworzących SFP stanowią:
-strzałka Pirsa (NOR),
-kreska Szefera (NAND).
Ponieważ każda z nich pojedynczo tworzy SFP.
Tablica wartości funkcji (tablica prawdy) -dla określenia wartości funkcji przełączającej należy podać jakie wartości funkcji przyjmuje ona dla każdego zespołu wartości funkcji. Ciąg wartości zmiennych będących ciągiem 0.1 może być traktowany jako liczba binarna lub można posługiwać się jej odpowiednikiem dziesiętnym
Alternatywna postać kanoniczna (kanoniczna postać sumy)
Koniunkcyjna postać kanoniczna (kanoniczna postać iloczynu)
Zależności te ułatwiają proste przejście od tablicy wartości funkcji do analitycznego zapisu funkcji.
Tak więc aby przedstawić funkcję w alternatywnej postaci kanonicznej należy wypisać z tablicy prawdy tylko te wiersze dla których funkcja ma wartość 1, przy czym zmienne przyjmujące wartość1 wchodzi do iloczynu w postaci afirmacji, a zmienna przyjmująca wartość 0 w postaci negacji.
MINIMALIZACJA FUNKCJI PRZEŁACZAJĄCYCH.
Otrzymane postacie kanoniczne pozwalają zrealizować daną funkcję przy pomocy elementów NIE,I,LUB. Jednak ponieważ w postaciach tych występują iloczyny bądź sumy pełne to realizacja ta będzie nieefektywna (będzie zawierać zbyt wiele wielowejściowych elementów) dlatego też ważnym etapem syntezy jest uzyskanie takiej postaci funkcji przełączającej, w której funkcja ta odwzorowując zadaną zależność logiczną zawiera minimalną liczbę liter. Proces poszukiwania takiej postaci funkcji nazywamy minimalizacją formalną funkcji.
Normalną postacią sumy (alternatywną postacią normalna APN) będziemy nazywać sumę różnych elementów iloczynów.
Normalną postacią iloczynu (koniunkcyjną postacią normalną KPN) nazywamy iloczyn różnych elementów sum.
Implikantem danej funkcji przełączającej nazywamy funkcję tych samych argumentów o następującej własności:
-dla wszystkich zespołów wartości argumentów dla których aplikant = 1 również dana funkcja = jest jedności.
Implicentem danej funkcji przełączającej nazywamy funkcję tych samych argumentów o następującej własności:
-dla wszystkich zespołów wartości argumentów dla których implicent jest = 0 funkcja również jest równa 0-ru.
Implikant (implicent) prosty - jest to implikant (implicent) bedący iloczynem (sumą) elementarnym, który zmniejszany o dowolną literę przestaje być implikantem (implicentem).
Minimalizacja funkcji przełączającej polegać będzie na przedstawieniu jej w postaci normalnej APN lub KPN zawierającej możliwie jak najmniejszą liczbę liter.
Można wykazać, że minimalną będzie postać zawierająca wyłącznie proste implikanty (implicenty) funkcji.
Suma (iloczyn) wszystkich prostych implikantów (implicentów) danej funkcji nazywa się jej postacią skróconą. Cęsto usunięcie niektórych prostych implikantów (implicentów) z postaci normalnej nie powoduje zmiany wartości funkcji . Postacie uzyskane z postaci skróconych przez rugowanie zbędnych implikantów (implicentów) nazywają się postaciami końcowymi. Postaci takich może być kilka. Co najmniej jedna z nich jest minimalną postacią normalną.
Wszystkie metody minimalizacji oparte są o reguły sklejania mówiące, że dwa elementarne iloczyny (elementarne sumy) można sklejać gdy mają one taką samą ilość liter i gdy różnią się między sobą tylko negacją jednej litery.
Ax + Anie-x=A-implikanty - dowolne iloczyny logiczne.
(B+x)(B+nie-x)=B implikanty
Dodatkowa w procesie minimalizacji wykorzystuje się procedurę niepełnego sklejania mówiącą, że jeden elementarny iloczyn (el. Suma) musi być wzięty do sklejania więcej niż jeden raz. Elementarne iloczyny, (el.sumy), podlegające sklejaniu, czyli różniące się negacją tylko jednej litery, nazywamy wyrażeniami sąsiednimi.
MINIMALIZACJA FUNKCJI PRZEŁĄCZAJĄCYCH METODĄ TABLIC CARNAFA.
Metodę tą można stosować do niewielkiej ilości zmiennych (do 6 zmiennych). Dzięki temu, że opis wartości zmiennych w tablicy Carnafa dokonany jest w kodzie Greaya ciągi wartości zmiennych opisujące klatki tablicy leżące obok siebie różnią się tylko na jednej pozycji, a więc odpowiednie pełne iloczyny (sumy) są wyrażeniami sąsiednimi.
PROSTE IMPLIKANTY (IMPLICENTY) w tablicy Carnafa wyznacza się łącząc ze sobą sąsiednie jedynki (zera) w grypy zawierające 2k klatek. Należy przy tym pamiętać, że brzegi tablicy również ze sobą sąsiadują. Wyznaczone grupy opisane są wyrażeniami elementarnymi (iloczynami albo sumami) w skład których wchodzą tylko te litery których wartość nie zmienia się w ramach grupy. Przy opisywaniu grupy obejmującej jedynki funkcji (prostego inplikantu) do iloczynu elementarnego w postaci afirmacji wchodzą zmienne, których wartość w ramach grupy = jest 1. Natomiast w postaci negacji wchodzą te zmienne których wartość w ramach grupy =0.
Przy wyznaczaniu prostego implicentu (grupa obejmuje 0 funkcji) do sumy elementarnej w postaci negacji wchodzą zmienne, których wartość w ramach grupy równa jest jedności. Natomiast w postaci afirmacji wchodzą te zmienne których wartość w ramach grupy równa jest zero.
Poszczególne grupy odpowiadające poszczególnym implikantom (implicentom) mogą zawierać kratki wspólne z innymi grupami (zgodnie z zasadą niepełnego sklejania). Klatki zawierające kreski mogą być łączone zarówno z jedynkami jak i zerami funkcji.
MINIMALIZACJA FUNKCJI PRZEŁĄCZAJĄCYCH METODĄ QINEA-MCCLUSKIEGO.
Metodę tę stosuje się przy większej ilości zmiennych (6-10) wadą metody jest konieczność rozłącznej minimalizacji alternatywnej koniunkcyjnej postaci kanonicznych.
W celu znalezienia minimalnej APN funkcji należy wykonać następujące czynności:
a)Przedstawione w postaci binarnej zespoły wartości argumentów ale których funkcja jest równa jedności lub nieokreślone, należy wypisać w kolumnie porządkując w.g. liczby jedynek w grupie w.g. kolejności jedynek. Ilość jedynek w grupie nazywamy indeksem. Poszczególne grupy o stałym indeksie należy oddzielić liniami.
b)Należy porównać ze sobą kolejne ciągi jedynek grupy ze wszystkimi ciągami następnej grupy, łącząc ze sobą ciągi różniące się jedną literą binarną. W wyniku połączenia powstaje ciąg z kratki w miejscu kolumny. Sklejane ciągi należy oznaczyć (co znaczy że nie są one implikantami prostymi). Jeśli któryś z ciągów nie da się połączyć z żadnym z innych to jest on implikantem prostym (pozostaje nieoznaczony).
c)W drugiej kolumnie wpisuje się wyniki wszystkich połączeń dokonanych w pierwszej kolumnie. Przy czym wyniki połączeń grupy 1i2 oddziela się kreską od wyników połączeń 2i3 i tak dalej. Następnie analogicznie jak poprzednio porównuje się kolejno ciągi z sąsiednich grup łącząc ze sobą ciągi różniące się jedną cyfrą (a więc mające kreski na tych samych pozycjach). Nie wolno łączyć ciągów mających kreski na różnych pozycjach.
d)Opisana procedura trwa dopóty, dopóki nie skończą się możliwości łączenia. W jej wyniku otrzymuje się zbiór wszystkich implikantów prostych, które można zamienić na postać literową.
FAKTORYZACJA - otrzymane w procesie minimalizacji końcowe postacie funkcji często można jeszcze dalej przekształcić, tak aby otrzymać mniejszą liczbę liter. Proces takiego przekształcenia nosi nazwę FAKTORYZACJI. Polega on na wyciągnięciu przed nawias wspólnego czynnika (w przypadku APN), albo częściowego wymnożeniu (w przypadku KPN). y=x1x2 +x1niex3=x1 (x2 +niex3)
y=(x1 +x1niex2)(x1 +x3)= x1 +x3 niex2
REALIZACJA UKŁADÓW NA ELEMENTACH LOGICZNYCH.
Elementarnym układem kombinacyjnym (bramką logiczną nazywamy układ kombinacyjny o dwóch wejściach i jednym wyjściu realizujący funkcję przełączającą dwóch zmiennych.
Każdy element logiczny jest wzmacniaczem.
Złożony kombinacyjny element logiczny otrzymujemy łącząc bramki zgodnie z następującymi zasadami:
-wyjście bramki może być dołączone do jednego lub więcej wejść innych bramek,
-wyjścia dwóch bramek nie mogą być łączone ze sobą bezpośrednio.
STRUKTURA ZAWODNOŚCI UKŁADÓW KOMBINACYJNYCH.
W rzeczywistych układach cyfrowych za wskutek istnienia opóźnień w elementach w chwili przełączania układu może nie być realizowana założona funkcja przełączająca pomimo poprawnego zaprojektowania układu.
Zjawisko występowania krótkotrwałego impulsu o przeciwnej polaryzacji niż założone w układzie jest skutkiem różnych czasów propagacji w elementach stykowych lub bramkowych logicznych i nosi nazwę HAZARDU STATYCZNEGO.
W pierwszym przypadku gdy nie jest zrealizowana zależność xniex=0 określany jest jako hazard statyczny w zerach (HSO). Natomiast w drugim przypadku gdy nie jest zrealizowana zależność x+niex=1, nosi nazwę hazardu statycznego w jedynkach (HS1).
Oprócz hazardu statycznego w układach o dużej liczbie poziomów może wystąpić HAZARD DYNAMICZNY polegający na wielokrotnym wystąpieniu krótkich fałszywych impulsów. Hazard ten można eliminować poprzez zmniejszenie liczby poziomów lecz zwykle nie jest to możliwe. Najbardziej radykalnym sposobem wyeliminowania hazardu jest synchronizacja układów kombinacyjnych umożliwiająca odczytanie stanu układu po zakończeniu wszystkich procesów przejściowych. Zjawisko hazardu należy zawsze eliminować gdy występujący krótkotrwały fałszywy sygnał może doprowadzić do błędnego działania układu (np. wtedy gdy sygnał ten steruje układem asynchronicznym. Natomiast w sytuacji gdy błędny impuls nie będzie podtrzymywany w dalszej części układu sterującego można hazardu nie eliminować (np. przy sterowaniu elementami optycznymi
SYNTEZA UKŁADÓW Z ELEMENTÓW NAND I NOR.
Elementy NAND i NOR są wzajemnie dzielne a więc układ z elementów NOR realizujący funkcję: y=f(x1,x2...xn) po zamianie elementów NOR na NAND bez zmiany struktury realizować będzie funkcję dualną y=f(niex1,niex2...niexn).
Realizacje postaci normalnych za elementach NAND albo NOR daje różną złożoność układu. W związku z tym chcąc otrzymać minimalną realizację układu należy uzyskać minimalną APN i KPN. Przy czym jeśli układ realizujemy na NAND-ach to należy:
-przy realizacji APN zamienić sumy i iloczyny na NAND-y zmienne wchodzące do sumy zanegować.
-przy realizacji KPN sumy i iloczyny zamienić na NAND-y i dodać negator na wyjściu układu. Zmienne wchodzące na sumy zanegować.
-Dekodery (deszyfratory) - są głównie stosowane do zmiany informacji np. z postaci binarnej na kod „1 z n” (jeśli na wybranym wyjściu jest jedynka), lub na kod „nie jeden z n” (jeśli na wybranym wyjściu jest zero).
MULTIPLEKSERY- układy kombinacyjne o n-wejściach i jednym wyjściu, przekazujące informację z jednego z wejść na wyjście zgodnie z adresem. Multipleksery mogą być pojedyncze tzn. przekazujące na wyjście sygnał z jednego wejścia lub grupowe tzn. przekazujące na wyjście grupę sygnałów, są tzw. multipleksery wielokrotne posiadające wspólne wej. adresowe. Stosowane są do realizacji funkcji przełączających.
DEMULTIPLEKSERY- są to układy o jednym wejściu i wielu wyjściach, przekazujące informację wejściową na jedno z wyjść zgodnie z adresem. Multipleksery idemultipleksery w układach cyfrowych mogą być wykorzystane jako generatory słów wejściowych.
MINIMALIZACJA TABLICY PRZEJŚĆ.
Tablica przejść wyjść zbudowana na podstawie grafu przejść lub opisu słownego nie zawsze mają minimalną liczbę wierszy, a ponieważ od liczby wierszy zależy wielkość pamięci, to układy zawierające minimalną liczbę wierszy będą prostsze i tańsze. Istnieje więc konieczność zminimalizowania liczby stanów wewnętrznych w każdej wstępnie uzyskanej tablicy przejść.
Proces minimalizacji liczby stanów wewnętrznych polega na zastąpieniu dwóch lub więcej wierszy, tablicy przejść jednym bez zmiany sposobu działania układu
Hazard
W układach asynchronicznych szczególnie groźne jest zjawisko hazardu. Często to spowodowane jest faktem, że każdy nieprawidłowy sygnał wejściowy może zostać podtrzymany przez sprzężenie zwrotne, a więc przy wyznaczaniu funkcji wzbudzeń należy zawsze grupy tworzyć tak aby eliminować zjawisko hazardu. Najprościej jest zbudować układ o dwóch stanach wewnętrznych ponieważ do jego zakodowania potrzebny jest jeden element pamięci, a więc żadne wyścigi nie mają miejsca.
Przedstawiona metoda kodowania najczęściej nie prowadzi do rozwiązania optymalnego ponieważ przyjęta w niej zasada pojedynczych zmian sygnałów elementów pamięci nie jest warunkiem koniecznym do usunięcia wyścigów krytycznych a ponadto metoda ta nie daje układów o minimalnej złożoności. Lepsze rezultaty można uzyskać stosując rachunek podziałów ponieważ w tej metodzie usuwa się wyścigi oraz uzyskuje się najprostsze postacie funkcji przej/wyj.
Hazard Jest groźny w ukł. asyn. Często to spowodowane jest faktem, że każdy nieprawidłowy sygnał wej. może zostać podtrzymany przez sprzężeni zwrotne, a więc przy wyznaczaniu funk. wzbudzeń należy grupy tworzyć tak aby eliminować zjawis. haz. Naneży zbudować ukł o 2-ch stanach wewn. ponieważ do jego zakodowania potrzebny jest 1-en ele. pamięci, a więc żadne wyści. nie mają miejsca.Przedstawiona metoda kodowania najczęściej nie prowadzi do rozwiązania optymalnego ponieważ przyjęta w niej zasada pojedynczych zmian sygnałów elementów pamięci nie jest warunkiem koniecznym do usunięcia wyści. kryty. a ponadto metoda ta nie daje ukł o minima. złożoności. Lepsze rezultaty można uzyskać stosując rach. podziałów ponieważ w tej metodzie usuwa się wyścigi oraz uzyskuje się najprostsze postacie funk. przej/wyj.
Rachunek podziałów.
Każdemu sygnałowi Qi odpowiada podział zbioru stanów wewnętrznych na dwa rozłączne podzbiory. Dla każdego jednego z nich Qi=0, dla drugiego Qi=1.
Podobnie każdy sygnał wyjściowy yi dzieli zbiór sygnałów wyjściowych na dwa rozłączne podzbiory.
Dla opisu tych rozłącznych podzbiorów stosuje się aparat matematyczny nazywany rachunkiem podziałów.
Definicje: Pokryciem zbioru C zbioru S nazywamy zbiór podzbiorów tego zbioru, których suma jest równa S.
C={ B1 , B2 , B... , Bn}
B1 ∪ B2 ∪ B... ∪ Bn = C
Podziałem π zbioru S nazywamy zbiór rozłącznych podzbiorów tego zbioru, których suma równa jest S
π={ B1 , B2 , B... , Bn}
B1 ∪ B2 ∪ B... ∪ Bn = C
Przecięcie zbioru i-tego ze zbiorem j-tym jest zbiorem pustym
Bi ∩ Bj = ∅ i ≠ j
Każdy podział jest pokryciem.
Podzbiory Bi nazywamy blokami i oznaczamy kreskami nad elementami tego podzbioru. W pewnych przypadkach wygodne jest wyróżnienie w podziale bloku którego elementy mogą być dołączone do dowolnych innych bloków podziału. Zwykle elementy tego bloku zapisuje się w nawiasach. Jeśli zbiór podziałów opisywany jest przy pomocy pokrycia w którym występują bloki w nawiasach, to każdy z elementów zapisanych w nawiasach można usunąć z jednego lub kilku nawiasów tak jednak, aby otrzymany zbiór bloków stanowił podział np.:![]()
to nie może być podziałem ( w podziale żaden element nie może być w różnych blokach 3,4)
Przykładowe podziały:
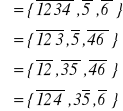
Iloczynem π1 • π2 podziałów π1 i π2 nazywamy podział, którego blokami są przecięcia bloków podziału π1 z blokami podziału π2 .
Przykład:
![]()
Sumą π1 + π2 podziałów π1 i π2 nazywamy najmniejszy podział π, taki że jeśli element si wchodzi do jakiegoś bloku z π1 lub π2 to cały ten blok musi zawierać się w którymś z bloków podziału π, a więc sumą jest podział, którego blokami są sumy nierozłącznych bloków π1 i π2.
Przykład:
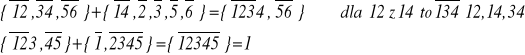
Podział π1 jest nie większy od podziału π2 czyli π1 ≤π2, gdy każdy blok podziału π1 jest zawarty w pewnym bloku podziału π2.
Przykład:
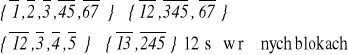
Największym i najmniejszym podziałem zbioru S = {1, 2, 3, ... , n } są odpowiednio:
podział jedynkowy ![]()
Zakodowanie zbioru stanów wewnętrznych S przy pomocy k sygnałów Q1, ... , Qk odpowiada k podziałów dwublokowych τ1, ... τk.
Jeżeli założymy, że chcemy realizować automat o minimalnej liczbie elementów pamięciowych to należy rozpatrywać tzw. podziały prawidłowe.
Podziały prawidłowe spełniają jednocześnie dwa warunki:
liczba bloków podziału wynosi 2,
liczba elementów bloku nie przekracza 2k-1.
Iloczyn tych podziałów musi być podziałem zerowym.
Rodziną końcową podziałów Tk nazywamy zbiór podziałów spełniających warunki zerowego iloczynu, który może być wzięty do kodowania.
W ogólnym przypadku rodzin końcowych może być wiele i potrzebna jest metoda wyboru rodziny wyznaczającej kod dający najprostsze funkcje przejść i wyjść, a więc w rezultacie najprostszą realizację układu.
Rodzina taka jest rodziną końcową optymalna Tkopt.
Na ogół zakłada się, że najprostszy układ uzyskujemy wykorzystując minimalna ilość elementów pamięci, a więc przy poszukiwaniu Tkopt należy uwzględniać jedynie podziały prawidłowe.
Przykład:
S = {1, 2, 3, 4 } ![]()
k=2 stąd 22-1 = 2 -liczba zmiennych potrzebnych do zakodowania
W tym przypadku możliwe jest utworzenie trzech podziałów prawidłowych:
![]()
ważne jest prawidłowe oznaczenie podziałów:
zapisuje się tym blokiem, który zawiera 1 lub mniejszą liczbę elementów np.:
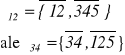
Tk1=τ12, τ13 ⇒ τ12 ° τ13 = 0
Tk2=τ12, τ14 ⇒ τ12 ° τ14 = 0
Tk3=τ13, τ14 ⇒ τ13 ° τ14 = 0
Weźmy teraz podział nieprawidłowy:
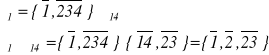
W sytuacji gdy jeden z podziałów tworzących rodzinę końcową będzie nieprawidłowym (liczba elementów przekroczy 2k-1 ) dla zapewnienia jednoznaczności kodowania (iloczyn podziałów =0)
Zmuszeni jesteśmy od odejścia od minimalnej liczby elementów pamięci.
Niezbędne więc staje się dodanie jeszcze jednego podziału aby zapewnić zerowy iloczyn (dodany podział może być podziałem prawidłowym jak i nieprawidłowym).
Podane warunki tworzenia rodziny końcowej mają różny ciężar gatunkowy. Warunek zerowego iloczynu podziałów jest warunkiem bezwzględnym, ponieważ niewypełnienie go prowadzi do baraku możliwości jednoznacznego zakodowania automatu (różnym stanom należałoby przyporządkować ten sam ciąg zerojedynkowy co wyklucza możliwość zakodowania).
Drugi z warunków (dotyczący użycia podziałów prawidłowych) jest zaleceniem umożliwiającym wykorzystanie do budowy układu minimalnej ilości elementów pamięci.
Parą podziałów π1 i π2 nazywamy uporządkowaną dwójkę podziałów taką, że dla każdych dwóch stanów zawartych w pewnym bloku z π1 i dla każdego xi ∈ X xi-te następniki tych stanów zawarte są w pewnym bloku z π2: π1 → π2.
Praktycznie przy kodowaniu postępuje się tak, że przyjmuje się pewien podział dwublokowy i dla niego poszukuje się poprzedników. Jeśli czynność tę przeprowadzi się dla dużej liczby podziałów τi to możliwe jest wyznaczenie kilku rodzin końcowych spośród których wyznacza się rodzinę końcową optymalną.
Wyznaczanie podziału π z pary π → τ (gdy dane jest τ ).
Buduje się kratę, której kreski pionowe odpowiadają kolumnom, a poziome wierszom tablicy przejść. Natomiast przecięcia odpowiadają klatce tablicy przejść. Na przecięciu kresek odpowiadającym klatce, w której występuje element pierwszego bloku podziału τ umieszcza się krzyżyk ×. Jeśli występuje wartość nieokreślona to na przecięciu odpowiadającym tym wartościom umieszcza się kółko o. Następnie pod kratą wypisuje się podział π będący poprzednikiem podziału τ.
Strukturę kratową buduje się dla wszystkich podziałów typu τ zawierających w bloku jeden element, dwa elementy, trzy elementy itd.. Jeśli liczba stanów przekracza 7 to strukturę kratową tworzy się tylko dla niektórych z wartości τ.
Przy kodowaniu dąży się do znalezienia takich podziałów aby f-cje przejść automatu zakodowanego zgodnie z tymi podziałami zależały od jak najmniejszej liczby zmiennych Qi.
Tzw. Niech τ1, τ2, ..., τi będą podziałami dwublokowymi wg których przyjmuje się wartości sygnałów Q1, Q2,...,Qi ; jeśli π → τ jest parą podziałów takich, że π ≥ τ1• τ2• ...• τj to Qj = σ((x1, x2, ..., xn; Q1, Q2, ... Q)
Wniosek z twierdzenia:
Aby funkcje przejść zależały od jak najmniejszej liczby argumentów należy szukać takich podziałów dla których spełnione są kolejno następujące warunki:
Podział jedynkowy poprzedza podział τj 1 → τj
Podział poprzedzający jest taki sam τj → τj
τi → τj - τi jest jednym z podziałów przyjętych do kodowania
π → τj π ≥ τ1 • τ2
π → τj π ≥ τ1 • τ2• τ3
π → τj π ≥ τ1 • ...•τk
Przez c( τj ) oznaczamy cenę podziału τj tzn. szacunkową ilość zmiennych, do których zależy funkcja wzbudzeń przerzutnika Qj zakodowanego zgodnie z τj pomniejszoną o jeden. Tak więc cenę podziału wewnętrznego τj będziemy wyznaczać jako n+l-1, gdzie n to liczba zmiennych wejściowych ( potrzebna do zakodowania wejść (np. x1, x2, x3 to n=2 bo potrzeba dwóch bitów ), l to liczba przerzutników, od których zależy wzbudzenie przerzutnika Qj.
Ceny te wyznacza się dla wszystkich podziałów wewnętrznych. Można założyć, że do kodowania należy brać podziały o zerowym iloczynie i minimalnej sumie cen podziałów.
Podział zewnętrzny πxj(yj) dla automatu Meale'go jest to podział, którego bloki zawierają tylko takie stany, którym przy stanie wejść xj odpowiadają jednakowe sygnały wyjściowe.
Dla automatu Moore'a można udowodnić twierdzenie analogiczne do tw. Podanego dla podziałów zewnętrznych tzn. że jeśli π(yj)≥ τ1• τ2• ...• τj, gdzie τ1,τ2,.. τj podziały wzięte do kodowania, to yi=λ(Q1, Q2,...,Qi).
Wyszukiwarka
Podobne podstrony:
System podatkowy WDW pytania
systemy rolnicze- kolokwium pytania, 1
Egzamin z pojęć i systemów pedagogicznych wszystkie pytania!
06. PLACÓWKI WSPOMAGAJĄCE FUNKCJONOWANIE RODZINY, Pytania do licencjata kolegium nauczycielskie w By
Karta audytu, system haccp trudne pytania proste odpowiedzi
Egzamin (niektore odp zle), Systemy Bezpieczenstwa Sieciowego - pytania, "Systemy Bezpieczeństw
Systemy energetyczne w Polsce, pytania dyplomowe
Systemy v01, EGZAMIN PYTANIA
wspolczesne systemy polityczne knopek pytania
caban,systemy operacyjne II, pytania egz
SystemyOperacyjne Funkcjenakolokwium(1)
Polityka społeczna i system ubezpieczeń społecznych (Pytania do zal.PSiSUS 2011 SUM), Notatki
systemy, 2 ko+éo-pytania, Ułożyć równanie reakcji:
systemy operacyjne egzamin pytania-odpowiedzi, !!!Uczelnia, wsti, materialy, II SEM
Podstawy Systemów Okrętowych Ściaga Pytaniami
System podatkowy WDW pytania
więcej podobnych podstron