Ćwiczenie 2.

Dyskretna transformata Fouriera (DFT). Sposoby wyznaczania i zastosowania.

Materiały pomocnicze:

1. Procedury służące do obliczania Dyskretnej Transformaty Fouriera i Odwrotnej Dyskretnej Transformaty Fouriera (Matlab 5.3):

Syntax (Składnia)

Y = fft(X)

Oblicza i umieszcza w wektorze Y Dyskretną Transformatę Fouriera obliczoną algorytmem FFT.

Y = fft(X,n)

Oblicza i umieszcza w wektorze Y n-punktową FFT (jeśli długość X jest mniejsza niż n, wektor X jest uzupełniany zerami, jeśli długość X jest większa to wektor jest skracany)

Y = fft(X,[],dim)

Y = fft(X,n,dim)

Wykonuje FFT „wzdłuż” wymiaru dim macierzy X.

.

.

Funkcje X = fft(x) oraz x = ifft(X)stanowią parę dysktretych transformat Fouriera (prosta i odwrotna) dla wektorów o długości N:

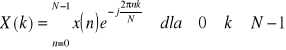
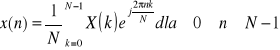
2. Procedury potrzebne do operacji na liczbach zespolonych:

1. complex c = complex(a,b) tworzy zespoloną liczbę (w zasadzie wektor) z dwóch liczb (wektorów) rzeczywistych i jest niezwykle użytecznym odpowiednikiem innego zapisu liczby zespolonej:

2. imag zwraca część urojoną liczby zespolonej

3. real zwraca część rzeczywistą liczby zespolonej

4. abs umożliwia wyznaczenie modułu liczby zespolonej

5. angle zwraca argument liczby zespolonej

6. conj wyznacza wartość sprzężoną liczby zespolonej.

3. Definicja splotu dyskretnego:

4. Definicja splotu funkcji dyskretnych okresowych (o okresie N):

W przypadku splotu funkcji okresowych można wykorzystać Twierdzenie o transformacie splotu dyskretnego: Jeżeli X₁(n) i X₂(n) są transformatami DFT okresowych ciągów x₁(n) oraz x₂(n), wówczas:

gdzie IDFT oznacza odwrotną transformatę dyskretną Fouriera.

Zadania do wykonania:

Zadanie 1

Wyznacz transformatę DFT ciągu {x_n} podanego przez prowadzącego. Naszkicuj widmo amplitudowo-fazowe.

{x_n}=.......................................

Porównaj transformatę uzyskaną własnym programem (skrypt Matlaba) ze standardową funkcją fft.

Zadanie 2

Wyznacz transformatę IDFT ciągu X(n) otrzymanego w poprzednim zadaniu.

Ułóż odpowiedni skrypt.

Zadanie 3

Wyznacz splot dyskretny sygnałów okresowych (N=4):

x₁(n)=............................................

x₂(n)=.............................................

Zastosuj:

1. Wzór definicyjny (wykorzystaj swój skrypt Matlaka z poprzedniego ćwiczena)

2. Twierdzenie o transformacie splotu (napisz odpowiedni skrypt).

Zadanie 4

Powtórz polecenia z Zadania 4 do sygnałów nieokresowych.

Czy Twierdzenie o transformacie splotu też można wykorzystać?

2

---