CIĄG ZAMKNIĘTY

1. Jeżeli ciąg nawiązany jest do dwóch punktów to obl. azymut początkowy A_p, który jest równy azymutowi końca A_k

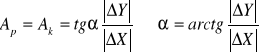
sprawdzamy z czwartakiem

2. Jeżeli ciąg jest, nienawiązany lub tylko jednopunktowo to muszę mieć pomierzony azymut początkowy A_p w terenie.

3. Obliczam sumę praktyczną [α]_p i teoretyczną [α]_t

kąty zewnętrzne

kąty wewnętrzne

4. Obliczam odchyłkę kątową f_kt jako różnicę sumy praktycznej i teoretycznej i porównuje ją z odchyłką dopuszczalną

dla ciągów o długości do 1,2 km

dla ciągów o długości ponad 1,2 km

Dla 30% ciągów można zwiększyć tolerancję i uwzględnić odchyłko dochodzące do 2*f_ktdop

5. Rozrzucam równomiernie otrzymaną odchyłkę kątową na poszczególne kąty. Każy pomierzony kąt otrzyma poprawkę v_kt wyrażoną w ” lub ^cc

n- ilość kątów pomierzonych w danym ciągu

Jeżeli dzielenie powoduje powstawanie reszty to zaokrąglamy poprawki raz w górę, raz w dół do pełnych ” lub ^cc, lecz przy tym należy doprowadzić sumę poprawek dokładnie do wartości odchyłki f_kt. Poprawki wpisujemy kolorem czerwonym.

6. Obliczam azymuty następne A_n na podstawie azymutu poprzedniego A_p
   i poprawionych kątów.

kąty lewe A_n = A_p + α - 200^g

kąty prawe A_n = A_p - β + 200^g

7. Obliczenie przyrostów

8. Kontrola przyrostów

s - sinus

c - cosinus

9. Obliczenie sum przyrostów praktycznych [Δx]_p [Δy]_p i teoretycznych [Δx]_t [Δy]_t

10. Obliczenie odchyłki liniowej f_L i porównanie jej z odchyłką dopuszczalną f_Ldop (G-4)

11. Rozrzucam odchyłki liniowe proporcjonalnie do długości boków

12. Obliczenie współrzędnych następnych współrzędnych X_n na podstawie współrzędnych punktu poprzedniego X_p i poprawionych przyrostów.

---