Rok akademicki: 1998/1999	Laboratorium z fizyki
Numer ćwiczenia: 71	Temat ćwiczenia: Promieniowanie cieplne.
Wydział: elektronika Kierunek: informatyka Grupa: 1.2	Imię i Nazwisko: Andrzej Zagubień
Data wykonania: 7. 04.1999 r.	Ocena:		Data zaliczenia:	Podpis:
		Teoria:
	Sprawozdanie:

1. Zasada pomiaru

Z prawa Kirchoffa wiadomo, że zdolność emisyjna ciał rzeczywistych jest mniejsza niż zdolność emisyjna ciała doskonale czarnego:

R - zdolność emisyjna ciała rzeczywistego

R - zdolność emisyjna ciała doskonale czarnego

a - współczynnik pochłaniania ciała

Z prawa Stefana-Boltzmana wiemy, że zdolność emisyjna ciała doskonale czarnego jest proporcjonalna do czwartej potęgi temperatury:

- stała Stefana-Boltzmana = 5,75 10^-8 Wm^-2K^-4

Emisja energetyczna ciała jest równa mocy wypromieniowywanej przez jednostkę powierzchni ciała R = P/S i po uwzględnieniu powyższych wzorów może być zapisana:

P = a S T⁴

Jeżeli temperatura otoczenia T0 jest niższa od temperatury ciała T, to wypromieniowuje ono moc:

P = a S ( T⁴ - T₀⁴).

W doświadczeniu wypromieniowywana moc jest absorbowana przez termoparę i wytwarza w jej obwodzie prąd elektryczny o mocy P_I proporcjonalnej do mocy P. Ponieważ P_I=U²/R, to P = f U².

Jeśli porównujemy dwa ciała: ciało badane i sadzę (w zakresie promieniowania widzialnego bardzo dobrze symulującą ciało czarne) znajdujące się w tej samej temperaturze zewnętrznej T₀, to:

dla ciała badanego:

dla ciała doskonale czarnego:

Ponieważ zarówno powierzchnia obu ciał, jak i temperatury są sobie równe, to po podzieleniu równań stronami otrzymujemy:

i przystępujemy do wyznaczenia współczynnika pochłaniania ciała badanego.

2. Układ pomiarowy

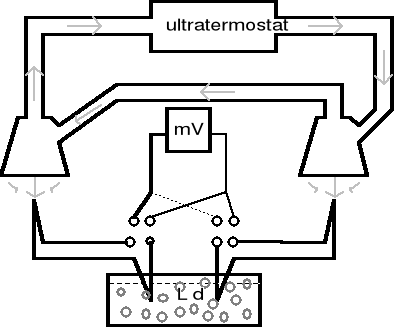
3. Ocena dokładności pojedynczych pomiarów

pomiar temperatury - termometr o dokładności 0,1C

pomiar napięcia - zarówno dla ciała badanego jak i dla sadzy wykonywany tym samym woltomierzem z odczytem cyfrowym - zmiana ostatniej cyfry: 0,001 V, ze względu na duże wahania przyjmujemy dokładność 0,01V

4. Tabela wyników

t	U	Uc	a
[°C]	[mV]	[mV]	-	-
60	0,1	0,2	0,25	0,00275
70	0,135	0,27	0,25	0,00275
80	0,171	0,337	0,257	0,00425
90	0,207	0,411	0,254	0,00125
			0,25275

5. Przykładowe obliczenia

pomiar 4:

T = 90C

U = 0,207 V

Uc= 0,411 V

a = 0,254

=

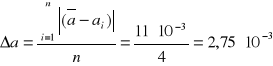
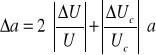
a4= 0,254 0,00105

6. Dyskusja błędów

Błędy (i ich przyczyny) zastosowanych przyrządów podałem już w punkcie 3:

T = 0,1C

U=Uc= 0,01V

Dodam tylko, że błąd pomiaru napięcia nie wynikał z niedokładności woltomierza, co raczej z niedokładności termopary, która nie nazbyt dokładnie izolowana reagowała na wszelkie zmiany temperatury otoczenia.

Błąd współczynnika a podany w rubrykach tabeli obliczyłem metodą różniczki logarytmicznej ze wzoru:

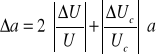
Błąd przeciętny podany dla średniej wartości współczynnika a (pod tabelą) obliczyłem ze wzoru:

Błąd obliczony za pomocą różniczki logarytmicznej jest mniejszy. Różnica ta wynika z tego, że błąd przeciętny obliczony jest dla średniej wartości wykonywanych pomiarów a błąd obliczony za pomocą różniczki logarytmicznej dla dowolnie wybranego pomiaru.

7. Zestawienie wyników

Wynik jest zgodny z zasadami teorii promieniowania termicznego, gdyż żadne ciało rzeczywiste nie może mieć stałej emisji większej od stałej emisji ciała doskonale czarnego, równej jedności.

a = 0,25275 0,00275

8. Wnioski

Ciało nagrzane do odpowiednio wysokiej temperatury ma zdolność świecenia, np. rozgrzane do białości ciecze lub ciała stałe wysyłają białe światło o widmie ciągłym. Przy obniżeniu temperatury świecącego ciała zmienia się nie tylko natężenie, lecz również skład widmowy promieniowania, przesuwając się w kierunku fal dłuższych (czerwonych lub podczerwonych). W miarę dalszego obniżania temperatury ciało przestaje wysyłać promieniowanie widzialne - wysyła natomiast niewidzialne promieniowanie podczerwone. Wyznaczony współczynnik pochłaniania zgadza się z danymi teoretycznymi, gdyż jego wartość jest mniejsza od jedności, którą posiada jedynie ciało doskonale czarne. Najbardziej idealnym modelem ciała doskonale czarnego jest niewielki otwór w nieprzezroczystej ściance zamkniętego naczynia.

2 Tomasz Rudnicki. Opracowanie doświadczenia 1994 / 95.

---