Wstęp
Przyciąganie pomiędzy ciałami odbywa się za pośrednictwem pola grawitacyjnego (pola ciężkości), które na równi z innymi polami fizycznymi i substancjami jest jedną z postaci materii. Charakterystyczną właściwością pola grawitacyjnego jest to, że na umieszczony w nim punkt materialny działa siła ciężkości wprost proporcjonalna do masy tego punktu. Wektorowo opisuje się pole grawitacyjne za pomocą natężenia g, które jest równe stosunkowi siły ciężkości G działającej na punkt materialny do wartości jego masy m:
Siła ciężkości punktu materialnego jest to siłą G równa różnicy wektorów siły F przyciągania tego punktu materialnego do Ziemi i siły dośrodkowej Fd, warunkującej uczestnictwo punktu materialnego w dobowym obrocie Ziemi:
przy czym
gdzie m - masa punktu, ω - prędkość kątowa dobowego obrotu Ziemi, R - promień Ziemi, ϕ - szerokość geograficzna miejsca obserwacji A.
Siła ciężkości jest maksymalna na biegunach i minimalna na równiku. Jednakże różnica ta nie przekracza 0.55%. Siła ciężkości ciała jest równa sumie geometrycznej sił ciężkości wszystkich punktów materialnych wchodzących w skład ciała. Punkt przyłożenia tej siły nazywa się środkiem ciężkości ciała, środek ciężkości ciała pokrywa się ze środkiem masy.
Swobodny spadek jest to ruch ciała, zachodzący pod wpływem tylko jego siły ciężkości. Przyspieszenie ziemskie grawitacyjne, (niekiedy zwane przyspieszeniem spadku swobodnego)
.
Jest ono jednakowe dla wszystkich ciał i zależy od szerokości geograficznej oraz wysokości nad poziomem morza. Wartość przyspieszenia ziemskiego g (w cm/s2) na niedużych wysokościach h (w metrach) n.p.m. można obliczyć ze wzoru przybliżonego:
Normalna wartość g przyjęta w obliczeniach barometrycznych i przy ustalaniu jednostek wynosi 0,80665 m/s2.
W większości obliczeń technicznych pomija się zależność g od ϕ i przyjmuje się g=9,81 m/s2, zaś do wyznaczania zmiany g zachodzącej podczas oddalania się od powierzchni ziemi stosuje się wzór przybliżony:
gdzie M - masa ziemi, R0=6370 km - średni promień Ziemi, zaś g0=9,81 m/s2.
Wahadło proste
Jest to odwzorowanie modelowego wahadła matematycznego. Wahadłem matematycznym nazywamy punkt materialny o masie m (kulka) zawieszony na nierozciągliwej i nieważkiej nici o długości l. W rzeczywistości każde wahadło musi być zbudowane w ten sposób, że nić jest nieco rozciągliwa i posiada pewną masę, a kulka metalowa zawieszona na tej nici jest większa od punktu matematycznego.
Rys. 1. Wahadło proste.
W czasie wychylenia kulki o kąt φ z położenia równowagi składowa styczna siły ciężkości będzie wyrażona wzorem:
![]()
.
Równanie ruchu harmonicznego wahadła prostego wyraża się wzorem:
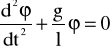
,
a rozwiązaniem tego ruchu jest funkcja:
![]()
,
gdzie φm - amplituda drgań, φ0 - faza początkowa.
Częstość spełnia warunek:
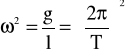
.
Okres drgań wahadła matematycznego wyraża się wzorem
![]()
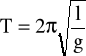
.
Okres ten nie zależy od masy wahadła, a zależność od amplitudy ma znaczenie dopiero dla dużych kątów.
Po przekształceniu wzoru na okres drgań wahadła matematycznego otrzymujemy:
![]()
.
Z tego przekształcenia wynika, że do wyznaczenia przyspieszenia, ziemskiego wystarczy zmierzyć długość wahadła i okres jego drgań. Aby uniknąć popełnienia błędu stosujemy tzw. wahadło różnicowe. Długość takiego wahadła możemy zmieniać, a zmiany te mierzyć stosunkowo dokładnie (np. katetometrem).
Mierząc dwukrotnie okresy drgań dla dwóch różnych długość otrzymamy dwa równania:
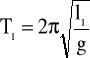
,
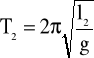
.
Po podniesieniu tych równań do kwadratu odejmujemy je i przekształcamy do postaci:
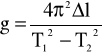
Wyszukiwarka
Podobne podstrony:
5427
5427
5427
5427
04wykladid 5427
5427
5427
5427
więcej podobnych podstron