Kaczor Łukasz 2006-01-22

Sprawozdanie z ćwiczenia nr 9

Sprawdzanie równania ruchu obrotowego brył

1. Zagadnienia teoretyczne

Kinematyka zajmuje się opisem ruchu ciał bez uwzględniania ich masy i rozpatrywania przyczyn, które ten ruch spowodowały. Dlatego w kinematyce opis ciał sprowadza się do opisu punktu materialnego. Przez punkt materialny rozumie się punkt geometryczny,
w którym skupiona jest pewna masa. Każde ciało dopóty może być punktem materialnym, dopóki nie bierze się pod uwagę szczegółów budowy tego ciała, jego kształtu, struktury wewnętrznej czy innych właściwości fizycznych.

Położenie jakiegokolwiek ciała określa się zawsze w stosunku do innego ciała, z którym wiążemy określony układ współrzędnych przyjęty za układ odniesienia. Mówiąc
o kinematyce rozważamy takie zagadnienia jak: prędkość liniowa (chwilowa) v punktu materialnego, czyli stosunek zmiany wektora wodzącego w czasie do czasu, w którym ta zmiana nastąpiła:

Gdy prędkość punktu zmienia się, czyli gdy ruch nie jest ruchem jednostajnym, wprowadza się do opisu ruchu przyśpieszenie liniowe
, które określa szybkość zmiany wektora prędkości poruszającego się punktu; zarówno jego wartości liczbowej, jak i kierunku:

Dynamika podobnie jak kinematyka zajmuje się opisem ruchu ciał, lecz jednocześnie wyjaśnia warunki oraz przyczyny, na skutek których ciała poruszają się lub pozostają w spoczynku. Ruchy ciał można nadal opisywać dla punktu materialnego, opisując tym sposobem jedynie ruch postępowy. Ciało porusza się ruchem postępowym, jeżeli jego poszczególne punkty zakreślają tory równe i wzajemnie równoległe. Drogi przebywane przez wszystkie punkty ciała w ruchu postępowym są równe, a więc jeśli znamy ruch jednego punktu ciała, to tym samym znamy ruch wszystkich punktów tego ciała, czyli ruch całego ciała.

U podstaw dynamiki leżą zasady sformułowane przez Newtona. Poniżej podam zasady dynamiki dla ruchu postępowego:

Pierwsza zasada dynamiki. Jeśli wypadkowa sił działających na ciało jest równa zeru (
), to nie może zmienić się jego prędkość, czyli nie może ono przyśpieszyć. Innymi słowy, jeśli ciało spoczywa, to pozostanie w spoczynku, a jeśli się porusza, to będzie się nadal poruszać z tą samą prędkością (to znaczy z prędkością o tej samej wartości i kierunku).

Druga zasada dynamiki. Siła wypadkowa działająca na ciało jest równa iloczynowi masy tego ciała i jego przyśpieszenia (
).

Trzecia zasada dynamiki. Gdy dwa ciała oddziaływują ze sobą, siły, jakimi działają one na siebie mają taką samą wartość bezwzględną i przeciwne kierunki.

W ruchu obrotowym mamy do czynienia z nieco zmodyfikowanymi zasadami dynamiki ruchu postępowego.

Pierwsza zasada dynamiki. Jeśli moment siły działającej na bryłę sztywną wynosi zero, to bryła sztywna pozostaje w spoczynku lub wykonuje ruch obrotowy jednostajny

Druga zasada dynamiki. Moment siły działającej na bryłę sztywną jest równy pochodnej momentu pędu względem czasu.

Trzecia zasada dynamiki. Jeśli na bryłę sztywną A działa bryła sztywna B pewnym momentem siły to bryła B działa na bryłę A momentem BA odwrotnym do momentu AB.

W niniejszym ćwiczeniu posłużono się wahadłem Oberbecka. Wahadło to jest obracającym się wokół swojego środka prętem lub krzyżakiem, do którego ramion można przyczepić ciężarki w odległości d od osi obrotu. Na osi wahadła o promieniu r nawinięta jest nić, która przechodzi przez blok, a zakończona jest uchwytem na ciężarki.

2. Wykonanie ćwiczenia

1. Zważono masę walca M i masę ciężarka m.

2. Przyrząd podłączono do sieci i uruchomiono przyciskiem W3.

3. Założono ciężarek, po czym maksymalnie rozsunięto walce do osi obrotu.

4. Ciężarek przemieszczono w górę, nawijając nić na większą ze szpulek, po czym skontrolowaliśmy i potwierdziliśmy, że układ znajduje się w stanie spoczynku.

5. Ustalono określoną wysokość spadania, wynoszącą 0,4 m.

6. Wciśnięto przycisk W2 co spowodowało uwolnienie wahadełka. Zmierzono czas pokonania drogi h przez ciężarek.

7. Wciśnięto przycisk W1, przez co wyzerowano wskaźnik miernika.

8. Przeniesiono ciężarek w górne położenie, po czym ponownie został wciśnięty włącznik W2.

9. Pomiary powtórzono pięć razy, w celu oszacowania średniego czasu spadania.

10. W naszym przypadku doświadczenie sprowadzało się do wyznaczenia czasu spadania ciężarka z wysokości 0,4m dla 6 odległości walców od osi obrotu (d). Wyniki pomiarów zapisano w tabeli pomiarowej.

Tabela pomiarowa

M [ kg ]	m [ kg ]	r [ m ]	h [ m ]	d [ m ]	d^2 [ m ]	t [ s ]	t^2 [ s ]	Ic [ kg ∙ m^2]	I [ kg ∙ m^2]
0,193	0,135	0,083	0,4	0,1416 0,1616 0,1816 0,2016 0,2216 0,2416	0,0201 0,0261 0,0330 0,0406 0,0491 0,0584	1,396 1,452 1,341 1,371 1,343 1,609 1,572 1,535 1,587 1,579 1,697 1,784 1,697 1,752 1,759 1,837 1,830 1,803 1,789 1,822 1,987 1,917 1,887 1,934 1,898 2,122 2,070 2,026 2,039 2,029	1,9488 2,1083 1,7983 1,8796 1,8036 2,5889 2,4712 2,3562 2,5186 2,4932 2,8798 3,1827 2,8798 3,0695 3,0941 3,3746 3,3489 3,2508 3,2005 3,3197 3,9482 3,6749 3,5608 3,7404 3,6024 4,5029 4,2849 4,1047 4,1575 4,1168	0,0028	0,0066 0,0078 0,0092 0,0107 0,0122 0,0139

3. Obliczenia

Obliczenia w tym ćwiczeniu sprowadzały się do kilku prostych rachunków.

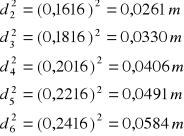
Następnie obliczono kwadraty czasu opadania ciężarka

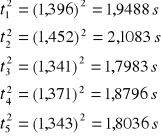
Po czym analogicznie obliczono czasy dla innych odległości walców od osi obrotu. Jeżeli
w układzie współrzędnych na osi y odkładamy t², a na osi x odkładamy wielkość d² wtedy mamy do czynienia z równaniem prostej y = Ax + B, gdzie

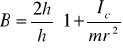
co wynika z równania

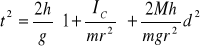
B daje wartość rzędnej w punkcie, w którym prosta przecina oś rzędnych. W naszym przypadku B = 1,04 s².

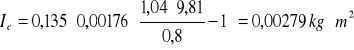
4. Wnioski

Na podstawie otrzymanych wyników, jak i zależności t² = f(d²) można stwierdzić, że doświadczenie zostało przeprowadzone w sposób w miarę dokładny. Różnice, które wystąpiły pomiędzy wartościami zmierzonymi w czasie wykonywania ćwiczenia, a podanymi wynikają między innymi z niedokładności przyrządów pomiarowych i błędów, które mogli popełnić przeprowadzający ćwiczenie. Pewną trudność stanowiło równomierne rozmieszczenie walców do osi obrotu.

---