Politechnika Rzeszowska
Katedra Automatyki i Informatyki
M. Wysocki
Zastosowanie obliczeń komputerowych w systemie MATLAB w teorii sterowania
System MATLAB
Wprowadzenie
Podstawowe elementy języka systemu MATLAB
Działania na macierzach
Instrukcja i wyrażenia
Operacje na elementach
Instrukcje i wyrażenia
Operacje na elementach macierzy
Relacje
Operacje logiczne
Inne operatory
Formaty wydruków
Tworzenie wykresów
Instrukcje sterujące przebiegiem programu
Zachowanie wyników obliczeń na dysku
Uzupełnienia podstawowych informacji
2. Przykłady zastosowań w teorii sterowania
2.1 Wielomiany
2.2 Transmitancja operatorowa
2.3 Wyznaczanie odpowiedzi skokowej
SYSTEM MATLAB
Wprowadzenie
1.1.1Informacje ogólne
System MATLAB umożliwia wygodne prowadzenie obliczeń matematycznych w zakresie różnych dyscyplin. Przydatność systemu uwidacznia się szczególnie w odniesieniu do problemów dotyczących teorii sterowania i teorii systemów. Obecnie system jest stale wzbogacany o nowe biblioteki procedur (TOOLBOX) obejmujące różne dziedziny jak sterowanie, przetwarzanie sygnałów, sieci neuronowe itd.
Uruchomienie systemu wymaga następującego zestawu komputera typu PC :
Minimum320kB pamięci operacyjnej
Przynajmniej jedna stacja dysków elastycznych
Koprocesor 8087, 80287 lub 80387
Zalecane jest też, aby zestaw posiadał dodatkowo:
Twardy dysk (MATLAB potrzebuje ok. 1,2 MB)
Większą pamięć operacyjną
Kartę graficzną SVGA
Rozpoczęcie pracy wymaga:
Odszukania katalogu zawierającego MATLAB (często odbywa się to automatycznie i jest realizowane przez system operacyjny )
Wprowadzenia z klawiatury polecenia uruchomienia systemu w postaci: MATLAB+Enter i poczekania na zgłoszenie się systemu przez wyświetlenie znaku „zaproszenia”: >>
Wyjście z systemu realizują instrukcje:
quit
exit
Podstawowe zasady pracy w systemie MATLAB
Duże i małe litery:
MATLAB rozróżnia duże i małe litery. Oznacza to, że np. A i a nie są tymi samymi zmiennymi. Wszystkie nazwy poleceń wprowadzanych po wyświetleniu na ekranie znaku „zaproszenia” >> muszą być pisane małymi literami. Instrukcją casesen można spowodować niewrażliwość na wielkość liter. Ponowne jej wywołanie przywraca stan początkowy.
Uzyskiwanie informacji pomocniczej systemu:
Instrukcja help <temat> powoduje wyświetlenie komentarza dotyczącego danego tematu. Pod nazwą <temat>
Wpisuje się na ogół nazwę procedury. Gdy napiszemy tylko help , nastąpi wyświetlenie tematów objętych tą instrukcją.
Uruchomienie przykładów demonstracyjnych:
Polecenie demo umożliwia prześledzenie istniejących już w systemie przykładów zastosowania wybranych funkcji MATLAB-a.
Wywołanie komend DOSu z poziomu MATLABa:
Rozpoczęcie polecenia od wykrzyknika ! oznacza, że dalsze napisy w linii oznaczają treść instrukcji dla systemu operacyjnego (DOS). Typowym przykładem jest wywołanie edytora ne poleceniem !ne.
Inne:
Średnik ; użyty po wyrażeniu lub instrukcji blokuje wyświetlanie wyniku na ekranie,
Dwie (lub więcej) kropki .. na końcu linii oznaczają kontynuację,
Przy edycji poleceń istnieją następujące możliwości:
% - oznacza, że dalsza część linii jest komentarzem,
- przywołanie poprzedniej linii
- przywołanie następnej linii
- przesunięcie kursora w lewo o jeden znak
γ - przesunięcie kursora w prawo o jeden znak
Ctrl - przesunięcie kursora o jedno słowo w lewo
Ctlrγ - przesunięcie kursora o jedno słowo w prawo
Home - przesunięcie kursora do początku linii
End - przesunięcie kursora na koniec linii
Esc - kasowanie całej linii
Ins - przełączanie między wstawianiem, a wpisywaniem w miejsce starego
Del - kasowanie znaku przed kursorem
Backspace -kasowanie znaku na lewo od kursora
Zbiory „.m” i „.mex”
Pocedury wykorzystywane przez MATLAB są zapisane w zbiorach z rozszerzeniami .m lub .mex. Rozszerzenie .mex mają procedury powstałe ze skomplikowanych programów w języku FORTRAN lub C, skonsolidowanych (zlinkowanych) do postaci wykonywalnej (.exe). Isnieje więc możliwość użycia własnych procedur napisanych w tych językach.
Obok możliwości wykorzystania FORTRANu i C, MATLAB, posiada własny język programowania, nazywany językiem systemu MATLAB, w którym także można pisać własne procedury(programy)rozszerzające biblioteki MATLABa. Procedury te przygotowuje się w postaci zbiorów źródłowych z rozszerzeniem .m, wykorzystując do tego celu edytor tekstowy(np. nc, ne, Sidekick itp.).Nie będziemy tutaj omawiać bliżej otrzymywania zbiorów typu .m, zawierających instrukcje języka systemu MATLAB.
Warto zaznaczyć, że podczas realizacji procedury źródłowe umieszczone w zbiorach typu .m nie są komplikowane lecz interpretowane, tzn. przed wykonaniem nie jest otrzymywany kod maszynowy taki, jaki zapewniają kompilatory i konsolidatory (linkery).W wyniku takiego podejścia MATLAB jest bardziej efektywnym systemem, którego zaletą jest eliminacja czasochłonnego cyklu kompilacja - konsolidacja-wykonanie. Z drugiej strony należy jednak zaznaczyć , że niektóre instrukcje ,zwłaszcza pętle, są wykonywane znacznie wolniej niż w językach kompilowanych jak C i PASCAL. Wydruk zbioru <nazwa . m> na ekranie uzyskuje się za pomocą polecenia type nazwa
Wydruk zbioru o dowolnym rozszerzeniu nazwa . roz otrzymuje się za pomocą polecenia type nazwa . roz.
Podstawowe elementy języka systemu MATLAB
Dla uproszczenia zamiast sformułowania ”język systemu MATLAB” będziemy używać skróconych postaci tej nazwy: ”język MATLAB” lub „MATLAB”
1.2.1Liczby w języku MATLAB
Zapis liczb rzeczywistych
Liczby są przedstawione w konwencjonalnym zapisie dziesiętnym z opcjonalną kropką dziesiętną i znakiem minus. Przykładami dozwolonego zapisu liczb rzeczywistych są:
3 -99 0.0001
9.6397238 1.60210E-20 6.02252e23
Każda liczba jest zapisywana w 8-miu bajtach, co umożliwia zapis z dokładnością około 16 cyfr znaczących. Zakres liczb wynosi w granicach od 10-308 do 10308.
Liczby zespolone
Aby wprowadzić liczby zespolone, trzeba wprowadzić jednostkę urojoną
i=sqrt(-1) lub j=sqrt(-1) .
Zapisu dokonuje się następnie w zwykły sposób, np.
3+4*j lub 5*exp(j*2.5)
Zmienne systemowe o stałych wartościach
eps=2-52=2.22*10-16 - wartość używana jako tolerancja, np. przy ocenie osobliwości macierzy; użytkownik może ją zmieniać na dowolną inną,
pi=π,
inf=∞,
NAN - „nie liczba” - uzyskiwana w operacjach Inf/Inf lub 0/0.
Macierze i działania na nich
MATLAB wykorzystuje w zasadzie tylko jeden typ obiektów, tj. prostokątne macierze liczbowe z dopuszczalnymi elementami zespolonymi. Szczególnym przypadkiem jest skalar, tzn. macierz 1x1 lub wektor, tj.macierz o jednej kolumnie lub jednym wierszu.
Wszystkie operacje w MATLABie rozumie się jako macierzowe. NA uwagę zasługuje fakt, że nie ma deklaracji zmiennych i rezerwowania wymiarów.
Wprowadzanie macierzy
Wprowadzanie macierzy może odbywać się następującymi sposobami:
Bezpośrednie podanie listy elementów z klawiatury,
Utworzenie zbioru .m,
Wywołanie instrukcji lub funkcji.
Przy wprowadzaniu małych macierzy najprościej jest podać listę elementów oddzielonych spacją lub przecinkiem zamkniętą w nawiasach prostokątnych, wewnątrz których wiersze są oddzielone średnikami.
Przykład 1.1
[ 1 2 3
A=[1 2 3 ; 4 5 6 ; 7 8 9 ] lub A= 4 5 6
7 8 9 ]
oznacza wprowadzenie macierzy A= 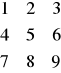
Zapis macierzy z przykładu 1.1 może być dokonany bezpośrednio z klawiatury, lub umieszczony wcześniej na dysku, np. w zbiorze macA.m . W drugim przypadku dla wprowadzenia macierzy do pamięci wystarczy instrukcja: >>macA (Enter)
Istnieje możliwość wykorzystywania już istniejących macierzy jeśli są one „podmacierzami” wprowadzanych macierzy; np. zapis :
A=[A;[ 10 11 12 ]]
Spowoduje, że macierz A będzie miała teraz postać: A=
Sposób wprowadzania macierzy z elementami zespolonymi ilustruje następujący przykład:
Przykład 1.2
Wprowadzanie jednego z poniższych zapisów:
A=[1 2 ; 3 4 ]+j*[ 5 6 ; 7 8 ] lub A=[1+5*j 2+6*j ; 3+7*j 4+8*j ]
Spowoduje to, że macierz A będzie miała postać: A= 1+5*j 2+6* j
3+7*j 4+8*j
Funkcje zapełniania prostych macierzy
Często spotykane można wprowadzić nieco prościej wykorzystując do tego celu specjalne funkcje(polecenia języka MATLAB). Należą do nich :
ones(n), ones(m,n), ones(A) - tworzą jedynek kolejno o wymiarach n, xn, mxn, takich jak znana macierz A.
eye(n), eye(m,n), eye(A) - tworzą macierze z jedynkami na przekątnej i zerowymi pozostałymi elementami o wymiarach jw.
zeros(n), zeros(n,m), zeros(A) - tworzą macierze z zer o wymiarach jw.
UWAGA: Jeśli A jest skalarem, to ones(A) ma taki wymiar jak wartość zapisana pod A. To samo dotyczy pozostałych funkcji.
Macierze puste
Macierz pusta (o wymiarach 0x0)może być zdefiniowana za pomocą operacji:
A=[].
Definiowanie wektorów
Ponieważ wektory także w MATLABie są traktowane jako szczególny przypadek macierzy może być dla nich stosowany dowolny spośród wyżej wymienionych sposobów wprowadzania. Dodatkowo wektory można tworzyć stosując specjalne zapisy języka MATLAB jak np.
x=1:5 jest równoważne utworzeniu wektora x=[ 1 2 3 4 5 ].
x=0:0.5:2 x=[ 0 0.5 1 1.5 2 ]
x=6:-1:1 x=[ 6 5 4 3 2 1 ]
Odwołania
A(i,j) element wiersza i oraz kolumny j macierzy A
A(1:5,3) wektor kolumnowy utworzone z pierwszych 5 elementów 3-ciej kolumny macierzy A
A(1:5,7:10) podmacierz macierzy A utworzona z pierwszych 5 wierszy i kolumn 7,8,9,10.
A(:,3) wektor utworzony z całej trzeciej kolumny
A(1:5,:) macierz utworzona z pierwszych pięciu wierszy.
Niech A i B oznaczają wcześniej wprowadzone macierze o wymiarach 10x10. Operacja podstawiania:
Niech A=
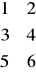
. Operacja podstawianiaOdwołanie może nastąpić przez wektory zero - jedynkowe. Niech A będzie macierzą mxn a L wektorem m - wyrazowym utworzonym z zer i jedynek. Wówczas odwołanie A(L,:) wyodrębni te wiersze macierzy, które odpowiadają niezerowym elementom L.
Działania na macierzach
odejmowanie
Transpozycja. Jeśli Z jest macierzą zespoloną, to Z' jest transpozycją z elementami sprzężonymi. Aby uzyskać transpozycję z wyjściowymi elementami trzeba zapisać Z'' lub conj(Z').
Dodawanie, odejmowanie, mnożenie. Dopuszczalne są operacje, gdy jeden z operandów jest skalarem. Wynik powstaje wtedy, jako rezultat działania na każdym z elementów macierzy. Przy mnożeniu macierzy wymaga się, jak zwykle, odpowiedniej zgodności wymiarów.
Dzielenie. Gdy macierz jest kwadratowa i nieosobliwa wynik jest otrzymywany przez rozwiązania odpowiednich układów równań. Gdy macierz jest bliska osobliwej w sensie wskaźnika uwarunkowania rcond(x) , pojawia się ostrzeżenie (rcond jest wtedy bliski zeru). Gdy macierz nie jest kwadratowa, wynik A\B uzyskuje się jako rozwiązanie układu AX=B w sensie aproksymacji metodą najmniejszych kwadratów (tzw. pseudoodwrotność)
Instrukcje i wyrażenia
Operacje na elementach macierzy
Mnożenie
10 18
Dzielenie
Potęgowanie
Relacje
Operacje logiczne
Inne operatory
Funkcje max i min
Formaty wydruków
0.0000
Tworzenie wykresów
plot(y) tworzy wykres wartości w funkcji indeksu
plot(x,y) tworzy wykres y w funkcji x (wektory mają te same wymiary).
plot(x,y,'*w')plot(x1,y1,x2,y2,...,xn,yn)
plot(x1,y1,':',x2,y2,'+')
Współrzędne logarytmiczne i biegunowe, oraz wykresy słupkowe
loglog wykres w skali log10-log10,
semilogx oś x w skali logarytmicznej (log10), oś y normalnie,
semilogy oś y w skali logarytmicznej (log10 ), oś x normalnie.
polar(thea,ro)
bar(x)
Podział okna ekranu
Ręczne skalowanie
axis
axis([xmin xmax ymin ymax]) lub axis(v)
axis(`sqare')
axis(`normal')
Wykresy trójwymiarowe
Sterowanie obrazem
shg przedstawienie okna graficznego;dowolny klawisz powoduje powrót do
clc wyczyszczenie okna poleceń;
clg wyczyszczenie okna graficznego;
home przestawienie kursora na początek.
Użycie drukarki
Instrukcje sterujące przebiegiem programu
pause powoduje wstrzymanie programu, aż użytkownik przyciśnie dowolny klawisz
pause(n) powoduje wstrzymanie na n sekund
Zachowanie wyników obliczeń na dysku
save nazwa
save nazwa A B C
load nazwa
diary nazwa
diary off
diary nazwa
clear wymazanie wszystkich zmiennych i funkcji
clear nazwa
clear nazwa1, nazwa2,...
clear function usuwa wszystkie aktualnie kompilowane funkcje typu `.m' z pamięci.
Uzupełnienia podstawowych informacji
Tworzenie własnych procedur
Wyświetlanie napisów
disp(X) wyświetla macierz X bez podawania jej nazwy, tzn. bez „X=”.
disp(`tekst') wyświetla tekst. Tekstem może być np. nagłówek tabeli.
Tworzenie menu
menu(s0,s1,s2,...,s15)
człon dwuinercyjny
człon oscylacyjny
Generowanie opóźnionego skoku jednostkoowego
y=stepfun(t,t0)
Przykłady zastosowań w teorii sterowania
Wielomiany
Pierwiastki
roots(w)
poly(r)
Transmitancja operatorowa
Rozkład na ułamki proste
Wyznaczanie odpowiedzi skokowej
MATLAB zapewnia wygodne odwoływanie się w programie do pojedynczych elementów lub fragmentów macierzy (wektorów). Ilustrują to następujące przykłady:
A(:,[ 3 5 10 ])=B(:,1:3) zastępuje 3,5 i 10 kolumny macierzy A trzema pierwszymi kolumnami macierzy B.
B=A(:) spowoduje utworzenie wektora b=![]()
. Odwołanie A(:)może być także użyte z lewej strony wyrażenia np.
A(:)=11:16 , co spowoduje, że nowa postać macierzy A będzie A=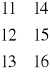
.
Wymiary macierzy
Wymiary macierzy x można odczytać za pomocą polecenia size(x) , [m,n]=size(x).
Długość wektora L otrzymuje się przez wprowadzenie length(L).
Podstawowymi działaniami na macierzach są:
` transpozycja (np. B=A', x=[ 1 2 3 ]', x=(0:1:4)')
+ dodawanie
* mnożenie
/ dzielenie prawostronne (X=A/B jest rozwiązaniem równania X*A=B)
\ dzielenie lewostronne (X=A\B jest rozwiązaniem równania A*X=B)
^ potęgowanie (ma ono postać A^p, gdzie A-macierz kwadratowa, p-skalar)
Komentarze
Prawostronną odwrotność B/A można interpretować jako (A'/B').
Instrukcja ma postać:
zmienna = wyrażenie
lub
wyrażenie
Wyrażenia składają się z operatorów, znaków specjalnych, funkcji i nazw zmiennych. Obliczenie wyrażenia powoduje otrzymanie macierzy wyświetlonej na ekranie (jeśli instrukcja nie została zakończona średnikiem). Gdy nazwa zmiennej i znak równości zostały pominięte tworzy się automatycznie zmienna ans , do której jest zapisywany wynik. Np. wprowadzenie z klawiatury wyrażenia :
>>1900/81
powoduje wyświetlenie
ans =
23.4568
Wprowadzenie wyrażenia (także dowolnego polecenia ) kończy się z chwilą wciśnięcia klawisza Enter. Jeśli jednak nie zmieściłoby się w jednej linii, trzeba przed wciśnięciem Enter wstawić przynajmniej dwie kropki „ .. ”. Puste miejsca wokół znaków = + - można wstawić dla przejrzystości zapisu. Należy jednak uważać w przypadku liczb zespolonych i rzeczywistych, np.
1 + 5*j - oznacza 2 liczby, a 1.23 e-4 jest błędem.
Jeśli zamiast zwykłych operacji macierzowych wykorzystujących symbole * / \ ^ ` zapiszemy operacje używając tych samych symboli poprzedzonych kropką, tzn. .* ./ .\ .^ .' , to będą one oznaczać działanie na odpowiadających sobie elementach macierzy. Oczywiście w odniesieniu do symboli + i - nie wprowadza się rozróżnienia, bo operacje na całych macierzach odpowiadają w tym przypadku operacjom na elementach macierzy.
Zakładamy, że macierze mają te same wymiary. Niech np. x=[1 2 3],y=[4 5 6].
Wprowadzenie do instrukcji
z= x. *y
powoduje
z=
z= x. \y lub z =y ./x daje
z=
4.0000 2.5000 2.000
z= x .^y daje
z=
1 32 729
Rozważmy jeszcze dwa przypadki szczególne:
1.Wykładnikiem jest skalar
Instrukcja z= x. ^2 daje w wyniku
z=
1 4 9
2.Podstawą jest skalar
z=2 .^[x y] lub z=(2) .^[x y].
W tym przypadku wynikiem jest
z=
2 4 8 16 32 64.
Podane poniżej funkcje matematyczne są wykonywane na poszczególnych elementach macierzy. Na przykład:
A=[1 4; 9 16 ], B=sqrt(A) powoduje B=[1 2 ; 3 4 ]
Spis funkcji matematycznych
abs wartość bezwzględna, moduł
sqrt pierwiastek kwadratowy
real część rzeczywista
imag część urojona
conj liczba zespolona sprzężona
round zaokrąglenie do najbliższej całkowitej
fix zaokrąglenie przez przesunięcie części ułamkowej
floor zaokrąglenie do najbliższej całkowitej (w dół)
ceil zaokrąglenie do najbliższej całkowitej (w górę)
sign funkcja signum {f(x)=1 dla x>0, 0 dla x=0, -1 dla x<0}. Dla x zespolonego
sign(x)=x./abs(x).}
rem reszta {Jeśli n =fix (x/y),to rem(x/y)=x-y.*n}
sin sinus
cos cosinus
tan tangens
asin arcus sinus
acos arcus cosinus
atan arcus tangens {-1/2π;1/2π}
atan2 arcus tangens {-π;π}
sinh sinus hiperboliczny
cosh cosinus hiperboliczny
tanh tangens hiperboliczny
exp funkcja wykładnicza o podstawie e
log logarytm naturalny
log10 logarytm dziesiętny
bessel funkcja Bessla
gamma funkcja gamma
rat aproksymacja wymierna { [a,b] = rat(pi) co daje a=355, b=113}
Przykład 1.3
Instrukcje A=[123;456],B=fix(pi*A),C=cos(pi*B), spowodują
A=![]()
, B=![]()
, C=![]()
Występuje 6 operatorów relacji służących do porównywania dwóch macierzy jednakowych wymiarów:
< mniejszy niż
<= nie większy niż
> większy niż
>= nie mniejszy niż
= = równy z
~ = różny od
Porównywanie odbywa się między odpowiadającymi sobie parami elementów, a rezultatem jest macierz jedynek i zer, przy czym 1 reprezentuje wartość logiczną „prawda”, a 0 reprezentuje wartość logiczną „fałsz”. Jeśli np.
A=![]()
, B=![]()
, to wynikiem operacji logicznej A<B jest macierz:![]()
.
Występują 3 operatory logiczne, które działają na elementach macierzy (zwykle zero - jedynkowych):
& AND (i)
| OR (lub)
~ NOT (nie)
Operatory AND i OR mogą być stosowane dla macierzy o jednakowych wymiarach. Wszystkie elementy niezerowe są traktowane jako „prawda”. W wyniku powstaje odpowiednia macierz zero - jedynkowa. Operator NOT jest operatorem negacji, ~A powoduje więc ustawienie zer w miejscach odpowiadających niezerowym elementom macierzy A, oraz jedynek w pozostałych miejscach.
1.8.1 Funkcje any i all
Jeżeli x jest wektorem, funkcja any (x) generuje 1, gdy wektor ma elementy niezerowe, 0 zaś w przeciwnym razie. Funkcjall (x)generuje 1, gdy wszystkie elementy wektora są niezerowe, 0 zaś w przeciwnym razie.
Jeżeli x jest macierzą, funkcje te operują na kolumnach macierzy i tworzą odpowiednie wektory wierszowe.
Są to instrukcje wyszukiwania maksymalnego i minimalnego elementu, przy czym mogą być stosowane następujące zapisy:
max(X) min(X)
[Y,I]=max(X) [Y,I]=min(X)
max(A,B) min(A,B)
Dla wektora X , max(X) jest maksymalnym elementem. Dla macierzy jest wierszowym wektorem złożonym z maksymalnych elementów kolumn. [Y,I]=max(X) podaje dodatkowo wskaźniki maksymalnych elementów zapamiętane w wektorze I. max (A,B) tworzy macierz o elementach będących większymi w parach odpowiednich elementów macierzy A,B.
W przypadku zmiennych zespolonych brane jest max(abs(X)). Funkcja min działa jak max z oczywistymi zmianami.
Jeśli wszystkie elementy macierzy są całkowite, ich wydruk ma zwykłą postać, tj. bez kropki dziesiętnej.
Jeżeli przynajmniej jeden element nie jest całkowity, postać wydruku zależy od przyjętego formatu.
format short (5 cyfr)
format short e (5 cyfr zmienno przecinkowych)
1.3333E+000 1.2345E-006
format long (15 cyfr)
1.33333333333338 0.000001234500000
format long e (15 cyfr zmienno przecinkowych)
1,33333333333338E+000 1,23450000000003E-006
format hex (hexadecymalnie)
3FF5555555555555 3EB4B6231ABFD271
format +
+ + (+ jeśli liczba dodatnia, - gdy ujemna, 0 gdy zero)
Przy długich formatach ostatnia cyfra może być niepoprawna, ale wynik jest dokładną dziesiętną reprodukcją liczby binarnej zapamiętanej w komputerze.
format compact pozwala ścieśnić zapis na ekranie, a tym samym wyświetlić więcej
informacji na ekranie
format loose oznacza powrót do luźniejszego wydruku
format powoduje przejście do formatu domyślnego, którym w MATLEBie jest
format short;
Formaty compact i loose nie zmieniają formatu numerycznego.
1.10.1 Wykresy dwuwymiarowe w zwykłych współrzędnych
Przedstawimy podstawowe możliwości, zakładając, że x i y są wektorami.
Przykład 1.4
x=0:0.05:4*pi;
y=sin(x)
plot(x,y);
punkty na wykresie y(x) są zaznaczone gwiazdką. W miejscu gwiazdki można umieścić następujące znaki: - linia ciągła,-- linia przerywana, : linia punktowa,-. Linia kreska - kropka oraz: . , + , * , o , x co powoduje tylko zaznaczenie punktów odpowiednimi znakami.
Litera `w' po gwiazdce oznacza kolor. Można określić następujące kolory: w - biały, b - niebieski, g - zielony, r - czerwony, i - niewidoczny.
W ten sposób jest otrzymywany wykres złożony z wielu przebiegów, gdzie x1,y1,x2,y2, - pary odpowiadających sobie wektorów; wektory w parze mają ten sam wymiar, ale nie oznacza to, że wymiary wektorów z różnych par mają być jednakowe. Każdy wykres jest rysowany inną linią.
Jest to wykres złożony z wielu przebiegów, przy czym typ linii dla poszczególnych przebiegów wybiera użytkownik.
UWAGA 1: Można też budować wykresy za pomocą instrukcji plot(X,Y), gdzie XiY sa macierzami. Nie będziemy jednak tego omawiać, gdyż przypadek ten da się zastąpić omówionymi poprzednio.
UWAGA 2: Utworzenie rysunku można opisać. Po instrukcji plot należy wtedy podać dodatkowe instrukcje definiujące postać wykresu, jak w poniższym przykładzie.
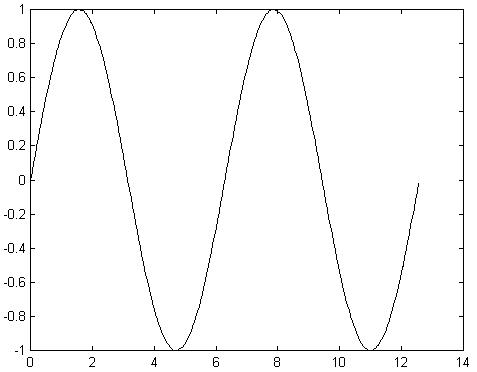
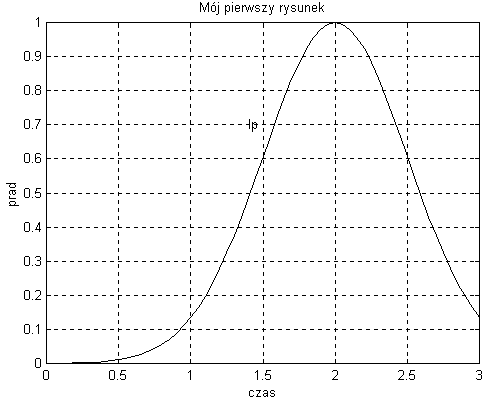
Przykład 1.5
t=0.0:0.05:3.0; - określanie obszaru zmienności argumentu
I=exp(-2*(t-2).^2); - wyznaczanie wartości funkcji
plot(t,I) - rysowanie wykresu
title(`Mój pierwszy rysunek') - nagłówek
xlabel(`czas') - opis osi x
ylabel(`prad') - opis osi y
grid - kratki (siatka w obszarze wykresu)
text(1.4,0.7,'Ip') - wpisanie tekstu wewnątrz okna w punkcie o współrzędnych
1.4,0.7(dokładniejsze informacje w help)
Można w ten sposób otrzymać wykres opisany jak na rysunku:
UWAGA 3: Gdy z jest wektorem zespolonym, plot(z) jest równoważne z plot(real(z),imag(z)).
W miejsce instrukcji plot można wstawić następujące (zapisywane w identyczny sposób) instrukcje:
Wykres we współrzednych biegunowych uzyskuje się przez
gdzie thea jest wektorem kątów w radianach, ro zaś promieniem. Instrukcję tę można zapisywać w wersjach podanych dla plot. Zlecenie grid powoduje wtedy wykreślenie siatki we współrzędnych biegunowych.
Instrukcja
tworzy wykres słupkowy elementów wektora. Nie dopuszcza się tu wielokrotnych wykresów.
Wykres uzyskany za pomocą podanych instrukcji zajmuje cały ekran. Można jednak tworzyć wykresy mniejsze oraz grupy wykresów. Wykorzystuje się wtedy instrukcję subplot. Sposoby jej użycia podano niżej:
subplot(121),plot(y1)
subplot(122),plot(y2)
subplot(211),plot(y1)
subplot(212),plot(y2)
Można też ekran podzielić na cztery części stosując instrukcję:
subplot(221),plot(y1)
subplot(222),plot(y2)
subplot(223),plot(y3)
subplot(224),plot(y4)
Instrukcja subplot(111) , lub zwyczajne subplot powoduje powrót do normalnego okna.
MATLAB daje możliwość skalowania ręcznego i automatycznego. Wykresy omawiane w poprzednich rozdziałach są wyskalowane automatycznie. Jeśli zachodzi konieczność ręcznego skalowania, używa się następujących instrukcji:
służy do zamiany trybu skalowania z automatycznego do ręcznego i odwrotnie. Wyjściowym stanem po uruchomieniu systemu jest „automatycznie”.
gdzie wektor v zawiera cztery elementy o tym samym znaczeniu, co uprzednio. Przy wykresach w skali logarytmicznej elementy wektora v są logarytmami dziesiętnymi z minimów i maksimów.
powoduje, że obraz jest kwadratowy, tzn. wykres y=x jest nachylony pod kątem 45 stopni, a wykres plot(sin(t),cos(t)) wygląda jak okrąg nie jak owal.
powoduje przejście do normalnego obrazu. Ta opcja jest wstawiana automatycznie po włączeniu systemu.
Istnieje możliwość graficznego przedstawienia funkcji dwóch zmiennych. Załóżmy, że zmienna x zmienia się od -π do π z krokiem 0.2. Podobnie zmienna y zmienia się od -π do π z krokiem 0.2.Niech ponadto:
z = sin(x) + cos(2y)
Wykres trójwymiarowy otrzymuje się za pomocą ciągu instrukcji:
[X,Y]=meshdom(-pi:0.2:pi,-pi:0.2:pi);
z=sin(x)+cos(2*y);
mesh(z)
title(`z=sin(x)+cos(2y)')
xlabel=(`x')
ylabel=(`y')
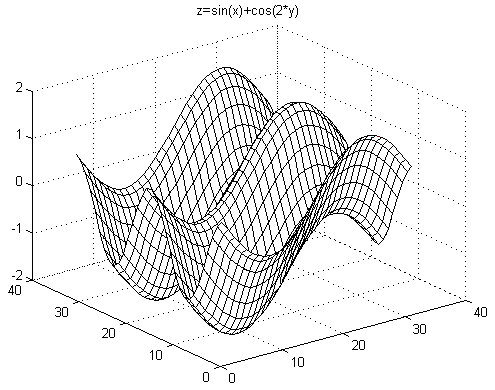
Instrukcja pierwsza i trzecia mają charakter ogólny. Pierwsza tworzy 2 macierze tj. X i Y. Jeśli na osi x występuje n punktów, a na osi y m punktów, to macierz X ma wymiary mxn i składa się z jednakowych wierszy, których elementy wyznaczają punkty wybrane na osi x. Macierz Y także o wymiarach mxn - składa się z jednakowych kolumn, których elementy wyznaczają punktom wybranym na osi y. Trzecia instrukcja powoduje powstanie wykresu. Dodatkowo za pomocą instrukcji contour(z) można wykreślić warstwice.
UWAGA. Istnieją możliwości obrotu powstałego wykresu trójwymiarowego. Informacje na ten temat można uzyskać korzystając z instrukcji help mesh.
Rozróżnia się dwie wersje ekranu: okno poleceń, w którym pracuje się normalnie i okno graficzne, w którym są wyświetlane wykresy. Przełączanie odbywa się za pomocą następujących instrukcji:
okna poleceń;
Kazda instrukcja plot powoduje wyczyszczenie ekranu i ustawienie nowego układu współrzędnych. Istnieje możliwość zatrzymania poprzednich wykresów przez wpisanie hold on. Następna instrukcja plot spowoduje wtedy dodanie nowych wykresów w starych współrzędnych. hold off usuwa tę możliwość. Można używać jedynie instrukcji hold, którą przełącza się z jednej opcji na drugą.
Jeśli sporządzone wykresy chcemy wydrukować na drukarce, należy przed uruchomieniem systemu MATLAB uruchomić program graph/c.
Wydruk obrazu przedstawionego następuje gdy wciśniemy lewy Shift
PrintScreen+F2.Wydruk tekstu z ekranu odbywa się po wciśnięciu lewy Shift
PrintScreen+F3.
1.11.1 Realizacja pętli typu for
Organizacja pętli jest następująca
for v= wyrażenie
instrukcje
end
Przykład 1.6 Przykład 1.7
for i=1:n for i+1:m
x(i)=0; for j=1:n
end A(i, j)=1/(i+j-1);
end
end
Przykład 1.8
for j=n-1:-1:1
A(:, j)= t. *A(:,j+1);
end
1.11.2Pętla typu while
Organizacja pętli jest następująca:
while wyrażenie
instrukcje
end
Przykład 1.9
Obliczymy ea za pomocą wzoru: ea=1+a+![]()
a2+![]()
a3+... z dokładnością do eps1, gdzie a i eps1 - zadane liczby. Odpowiedni program może mieć postać:
E=0.; F=1.; k=1;
while .F >eps1
E=E+F;
F=a*F/k;
k=k+1
end
1.11.3 Instrukcje if i break
Ogólna postać instrukcji if: Uproszczona postać instrukcji if:
if wyrażenie if wyrażenie![]()
instrukcje instrukcje
elseif end
instrukcje
else
instrukcje
end
Przykład 1.10 Przykład 1.11
if n<0 for i=1:n
A=-1; for j=1:n
elseif n==0 if i==jj
A=0; a(i,j)=2;
else elseif abs(i,-j)==1
A=1 a(i,j)=-1
end else
a(i,j)=0 end
end
end
Instrukcja break przerywa realizację pętli for i while. W przypadku pętli zagłębionych, break istnieje tylko dla pętli najbardziej zagłębionej.
Przykład 1.12
eps=1;
for i=1:1000
eps=eps/2;
if (eps+1<=1)
break end
end
eps=eps*2.
1.11.4 Instrukcje pause, keybord, input
Typowe zastosowanie instrukcji wiąże się np. z przyglądnięciem rysunkowi, który inaczej zniknąłby w związku z dalszymi obliczeniami.
Przykład 1.13
t= -300:300;
plot(t.*sin(t),t.*cos(t));
pause;
plot(rand(1,2000),rand(1,2000),'.');
title(`gwiezdna noc');
pause
Do przechowywania zbiorów na dysku służą instrukcje:
Pierwsza z nich aktualne zmienne w zbiorze o podanej nazwie z rozszerzeniem „.mat”. Druga instrukcja powoduje przechowanie zmiennych w linii polecenia.
Odtworzenie przechowywanych zbiorów w następnej sesji MATLABa jest możliwe dzięki instrukcji:
Istnieje także możliwość przechowywania na dysku przebiegu sesji. Instrukcja:
powoduje zapisywanie do zbioru o podanej nazwie komend z klawiatury i większości wyników (wyłączając rysunki ). Zapis jest dokonywany w kodzie ASCII, co umożliwia dokumentowanie. Instrukcja:
przerywa zapisywanie, a
ponownie je przywraca, zaś diary bez parametrów służy do przełączania między on i off. Do wymazywania danych z pamięci służą instrukcje:
Przedstawione wcześniej informacje o charakterze ogólnym pozwalają na samodzielną pracę z systemem MATLAB. W tym puncie zostaną podane wybrane dodatkowe elementy języka przydatne w sastosowaniach MATLABa w teorii sterowania.
1.13.1 Tworzenie własnych funkcji
Tworzymy zbiór o przykładowej nazwie mojaf.m. Pierwszy wiersz tego zbioru zapisujemy w formie:
function[x,y,z] = mojaf(a,b,c,d)
Dalsza część zbioru zawiera potrzebne instrukcje, w tym te, które nadają wartości zmiennym x, y, z.
Wywołanie funkcji dla parametrów aktualnych ma postać:
[xa,ya,za] = mojaf(aa,ba,ca,da).
Ilość parametrów formalnych po obu stronach zależy od użytkownika. W przypadku, gdy występuje tylko jeden parametr wyjściowy, np. x, to przy wywołaniu funkcji można pominąć[].
Wielokrotnie powtarzany ciąg instrukcji wygodnie jest zapisać w zbiorze typu `.m' i spowodować wykonanie tych instrukcji (wywołać ) podając nazwę zbioru jako polecenie.
Służy do tego celu instrukcja
gdzie sk są łańcuchami.
Przykład 1.14
k=menu (`podaj typ' , 'człon dwuinercyjny' , 'człon oscylacyjny')
spowoduje napis:
- - - podaj typ - - -
Select a menu number
Wybór liczby z menu powoduje podstawienie jej wartości pod k.
t jest wektorem tworzącym oś x. Powyższa funkcja nadaje y wartość 0, gdy t<t0, a wartość 1 wówczas, gdy t![]()
t0.
2.1.1 Zapis podstawowy
Wielomiany w systemie MATLAB są przedstawiane jako wektor wierszowy współczynników tych wielomianów zapisanych kolejno, rozpoczynając od stojącego przy najwyższej potędze.
Przykład 2.1
Wielomianowi: s3+3s2+5s+2 odpowiada wektor : w=[1 3 5 2]
Mając wielomian charakterystyczny przedstawiony w postaci wektora w, możemy wyznaczyć jego pierwiastki za pomocą instrukcji:
Wynik jest tworzony w postaci wektora kolumnowego.
Przykład 2.2
W odniesieniu do wielomianu z poprzedniego przykładu wyrażenie
r=roots(w)
-1.2267+1.4677*j
jest równoważne z utworzeniem wektora r = -1.2267-1.4677*j
-0.5466
Użycie funkcji:
gdzie r jest wektorem kolumnowym, spowoduje utworzenie wektora wierszowego przedstawiającego wielomian, którego pierwiastki podano w wektorze r. Wielomian ten ma przy najwyższej potędze współczynnik 1.
Przykład 2.3
Wyrażenie
ww=poly(r)
gdzie r określono w poprzednim przykładzie, spowoduje utworzenie wektora:
ww=[1.0000 3.0000 5.0000 2.0000].
2.2.1 Zapis w formie ilorazu wielomianów
W celu określenia transmitancji w formie ilorazu wielomianów podaje się dwa wektory charakteryzujące te wielomiany.
Przykład 2.4
Rozważamy transmitancję:![]()
Powyższą transmitancję zapisuje się w MATLABie przez podanie dwóch wektorów, przedstawiających licznik i mianownik:
LG=[3 2 ] MG=[3 5 2 1].
UWAGA: LG można też zapisać jako [0 0 3 2]. Wtedy oba wektory mają jednakowe wymiary.
Tansmitancję (lub transformatę Laplace'a) zapisaną w formie ilorazu wielomianów:
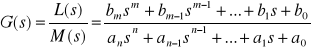
można również przedstawić wyodrębniając zera i bieguny. Ma ona wtedy postać:
![]()
z której przy założeniu jednokrotnych biegunów można otrzymać rozkład na ułamki proste postaci:
![]()
W typowym przypadku zachodzi nierówność n>m, tzn. rząd mianownika jest większy od rzędu licznika. Wtedy k(s)=0. W prze4ciwnym razie k(s) jest wielomianem takim, że L(s)/M(s)=L~(s)/M(s)+k(s), a stopień wielomianu L~(s)jest równy co najwyżej n-1. Liczby r1,...,rn, w ogólnym przypadku zespolone, są nazywane residuami.
Jeśli bieguny transmitancji są jednokrotne można uzyskać jej rozkład na ułamki proste wykorzystując następującą instrukcję MATLABa:
[r,p,k] = residue(l,m)
Wektory r i p są kolumnowe. Zawierają one residua (wektor r) i odpowiadające im bieguny (wektor p).Wierszowy wektor k charakteryzuje wielomian - resztę. Wierszowe wektory l i m odnoszą się do licznika i mianownika.
Funkcję residue można wykorzystać w drugą stronę. Zapisujemy wtedy:
[l,m] = residue (r,p,k)
co powoduje przejście z ułamków prostych (2.3) do postaci wielomianowej (2.1). Znaczenie wektorów jest takie, jak poprzednio.
W celu określenia odpowiedzi skokowej układu o podanej transmitancji wykorzystuje się instrukcję:
y=step (l,m,t)
gdzie y jest wektorem odpowiedzi w momentach opisanych przez elementy wektora t, odpowiadające równoodległym punktom na osi czasu. Wektory l i m określają transmitancję przez współczynniki wielomianów licznika i mianownika.
Przykład 2.5
Wyznaczyć odpowiedź skokową układu ![]()
w przedziale[0,10].
t=0:.01:10;
l=[5 1];
m=[1 2 2]
y=step(l,m,t)
plot(t,y)
title(`Odpowiedź skokowa `)
xlabel(`t')
ylabel(`y')
grid.
Wynikiem jest następujący wykres:
Wyszukiwarka
Podobne podstrony:
wersja do nauki, Studia - inżynieria & ochrona środowiska (inż. mgr.), Technologie wody i ścieków, P
materiał do nauki, Szkoła, przydatne w szkole
Pożar wiadomości, STRAŻ POŻARNA, Coś Do Nauki, TDG
Metodologia plik do nauki
wersja do nauki, Studia - inżynieria & ochrona środowiska (inż. mgr.), Technologie wody i ścieków, P
(1) Wprowadzenie do nauki o finansach 1id 778 ppt
kolocki logo do nauki, glottodydaktyka
komentarze do testów z przedsiębiorczości, podręczniki szkoła średnia liceum technikum klasa 3 trzec
elektryka, Kierunki studiów, Architektura, Materiały do nauki=), Budownictwo, Segregacja tematyczna,
test z przedmiotu wstep do nauki o panstwie i prawie (1), testy, wstęp
X Wykładnia prawa ćw, Politologia, Wstęp do nauki o państwie a prawie, Ćwiczenia
ppj - wypisywanie liczb pierwszych w javie, Do nauki, Pytania, rozwiązania, prace
Wydalanie i regulacja do nauki, WSKFIT 2007-2012, V semestr, fizjologia człowieka
Pytania - OTWP 81pyt, OTWP - Ogólnopolski Turniej Wiedzy Pożarniczej - Materiały do nauki
WIERSZYK DO NAUKI PIERWSZEJ POMOCY
wszysko do nauki wtorek
DO NAUKI Zarządzanie jakością
więcej podobnych podstron