Materiały pomocnicze do ćwiczeń laboratoryjnych z przedmiotu

Sygnały i Systemy Dynamiczne.

Ćwiczenie 2.

Analiza stanów dynamicznych systemów LTI z wykorzystaniem narzędzi środowiska programistycznego Matlab.

Problemy programistyczne (dla Matlaba 5.3)

1. Jak wyznaczyć odpowiedź układu LTI na dowolne wymuszenie?

2. Jak wyznaczyć charakterystyki częstotliwościowe?

Problem 1.

Ze względu na ograniczone możliwości dostępnej wersji Matlaba (brak narzędzi do analizy symbolicznej Symbolic Math Toolbox) wykorzystamy jedynie dostępne procedury rozkładu funkcji wymiernej na ułamki proste. Koncepcja metody została wyjaśniona w materiałach do Ćwiczenia 1. Przypomnijmy:

funkcję wymierną X(s) można rozłożyć na ułamki proste za pomocą funkcji residue:

Syntax (Składnia)

[r,p,k] = residue(L,M)

Argumenty

L,M	Wektory zawierające współczynniki wielomianów uporządkowane w kolejności malejących potęg s
r	Wektor kolumnowy residuów
p	Wektor kolumnowy zer
k	Wektor wierszowy składników bezpośrednich (gdy stopień licznika jest >= od stopnia mianownika)

Gdy wielomian reszty (k) jest pusty, funkcję wymierną (4) można zapisać w postaci:

(1)

Wówczas transformatę odwrotną Laplace'a można przedstawić jako

(2)

Uwaga: Stosowalność wzoru (2) ograniczona jest do biegunów jednokrotnych! (powyższa procedura wymaga wówczas modyfikacji).

Przykładowy plik zawierający rozwiązania problemu transformaty odwrotnej funkcji wymiernej X(s)=L(s)/M(s):

%Rozwiązanie za pomocą Transformaty Laplace'a

L=[2 -1 13 -4];

M=[2 3 12 12 16];

t=[0:0.1:20];

[r,p,k]=residue(L,M);

u=0;

for i=1:length(r)

u=u+r(i)*exp(t.*p(i));

end

plot(t,u),grid,xlabel('t'),ylabel('x(t)')

W przypadku poszukiwania odpowiedzi układu opisanego transmitancją H(s), korzystamy z zależności:

(3)

gdzie: X(s) jest transformatą sygnału wejściowego, H(s) zdefiniowaną w poleceniu 1 transformatą układu (czwórnika LTI) a Y(s) transformatą odpowiedzi.

Do uzyskania odpowiedzi impulsowej (ale i każdej innej) można też zastosować funkcję impulse

Syntax (Składnia)

impulse(sys)

impulse(sys,t)

[h,t]=impulse(sys).

Wekor h zawiera ciąg wartości odpowiedzi w puntach określonych przez wektor t, przykładowo: t =0:dt:Tfinal

Do uzyskania odpowiedzi skokowej można zastosować funkcję step

Syntax (Składnia)

step(sys)

step(sys,t)

[h,t]=step(sys).

Uwaga: Zmienna sys określa sposób opisu układu dynamicznego. Zapis: sys=tf(L,M) umożliwia zastosowanie standardowego, wielomianowego opisu transmitancji układu.

Przykład 1

%Odpowiedź impulsowa przy zerowych warunkach początkowych

%układu o transmitancji

%H(s)=s+3/(s^2+5s+6)

L=[1 3]

M=[1 5 6]

sys=tf(L,M);

Tmax=5;

td=0.1;

t=0:td:Tmax;

y1=impulse(sys,t)

y2=step(sys,t)

subplot(2,1,1);plot(t,y1);grid;ylabel('odpowiedź impulsowa');

subplot(2,1,2);plot(t,y2);grid;ylabel('odpowiedź skokowa')

pause

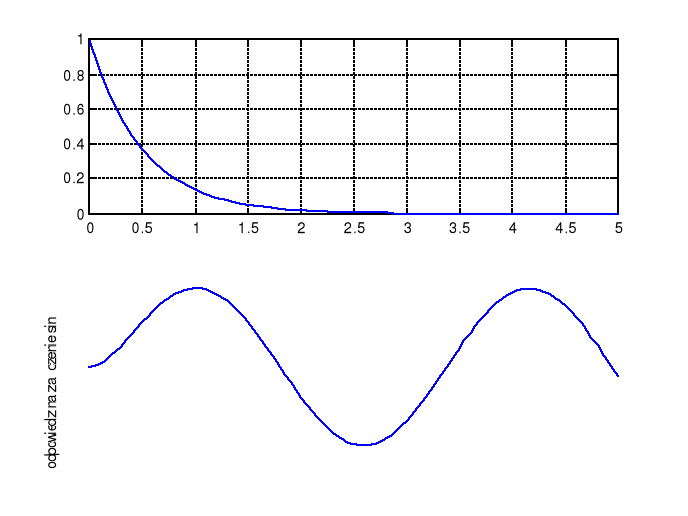
%odpowiedź na wymuszenie w postaci funkcji x(t)=exp(-2t)

%Y(s)=X(s)*H(s)=(s+3)/(s^2+5s+6)(s^2+1)

L=[1 3]

M=[1 5 7 5 6]

sys=tf(L,M);

Tmax=10;

td=0.1;

t=0:td:Tmax;

y3=impulse(sys,t)

plot(t,y3);grid;ylabel('odpowiedz na załączenie sin');

Przykład 2

Wyznaczanie składowej swobodnej i wymuszonej odpowiedzi układu

o transmitancji:

o wymuszeniu

Rozwiązanie:

Transformata odpowiedzi operatorowej układu jest postaci:

Realizacja Matlabowa:

1.Odpowiedź całkowita:

%Odpowiedź y(t) układu (wersja 1 implementacji)

L=[2 6];

M=[1 5.5 8.5 3];

t=[0:0.1:15];

[r,p,k]=residue(L,M);

u=0;

for i=1:length(r)

u=u+r(i)*exp(t.*p(i));

end

plot(t,u),grid,xlabel('t'),ylabel('y(t)')

lub

%Odpowiedź y(t) układu (wersja 2 implementacji)

L=[2 6]

M=[1 5.5 8.5 3]

sys=tf(L,M);

Tmax=15;

td=0.1;

t=0:td:Tmax;

y3=impulse(sys,t)

plot(t,y3);grid;ylabel('odpowiedz y(t)');

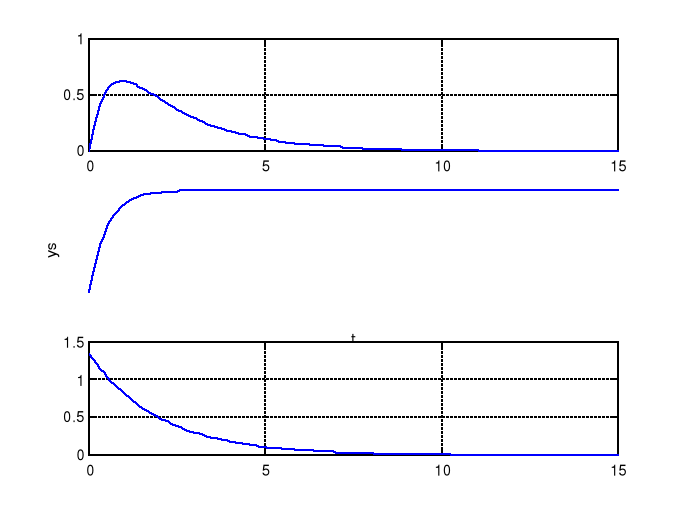
2.Odpowiedź swobodna i wymuszona (ustalona)

Rozwiązanie Matlabowe (rozkład na ułamki proste)

r =

3.907985046680596e-015

-1.333333333333336e+000

1.333333333333332e+000

p =

-2.999999999999995e+000

-2.000000000000004e+000

-4.999999999999999e-001

%Przykładowy m-plik

%Odpowiedź układu

L=[2 6];

M=[1 5.5 8.5 3];

t=[0:0.1:15];

[r,p,k]=residue(L,M)

u=0;

u1=0;

u2=0

for i=1:length(r)

u=u+r(i)*exp(t.*p(i));

end

for i=1:(length(r)-1)

u1=u1+r(i)*exp(t.*p(i));

end

for i=3:length(r)

u2=u2+r(i)*exp(t.*p(i));

end

subplot (3,1,1);plot(t,u),grid,xlabel('t'),ylabel('y(t)')

subplot (3,1,2);plot(t,u1),grid,xlabel('t'),ylabel('skladowa swobodna')

subplot (3,1,3);plot(t,u2),grid,xlabel('t'),ylabel('skladwa wymuszona')

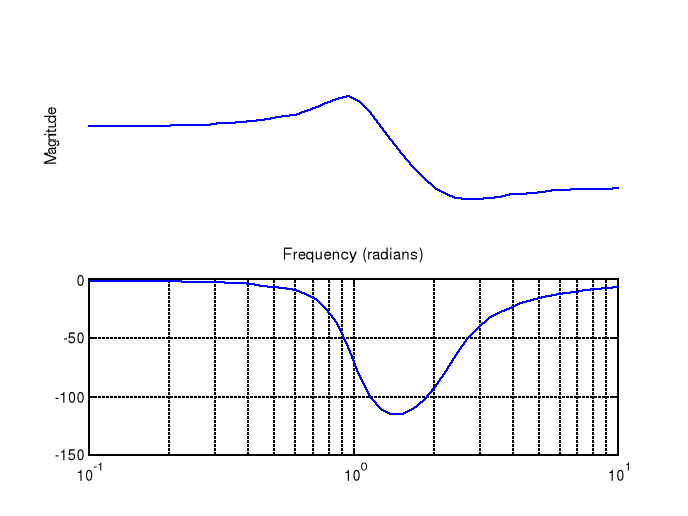
Jak wyznaczyć widmo amplitdowo-fazowe transmitancji

Rozwiązanie w skali logarytmicznej:

%Odpowiedź częstotliwościowa w skali logarytmicznej

%Zadanie H(s)=(0.2s^2+0.4s+1)/(s^2+0.4s+1)

M = [1 0.4 1];

L = [0.2 0.3 1];

omega = logspace(-1,1);

freqs(L,M,omega)

Inna implementacja:

%Odpowiedź częstotliwościowa w skali logarytmicznej -- inaczej

%Zadanie H(s)=(0.2s^2+0.4s+1)/(s^2+0.4s+1)

M = [1 0.4 1];

L = [0.2 0.3 1];

omega = logspace(-1,1);

h=freqs(L,M,omega);

mag = abs(h);

phase = angle(h);

subplot(2,1,1), loglog(w,mag);grid

subplot(2,1,2), semilogx(w,phase);grid;

1

Biegun wymuszenia

Bieguny transmitancji

---