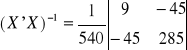Zadanie 1

W latach 1996-2002 (kwartalne dane) zaobserwowano następujące wielkości produkcji systemów komputerowych. Sformułowano hipotezę, że wzrost produkcji systemów komputerowych przebiegał według trendu liniowego. Mając dany raport Excela - Analiza regresji odpowiedz na poniższe pytania.

PODSUMOWANIE - WYJŚCIE
Statystyki regresji
Wielokrotność R	0,9945932
R kwadrat	0,989215634
Dopasowany R kwadr	0,988766285
Błąd standardowy	1,068143876
Obserwacje	26
ANALIZA WARIANCJI
	df	SS	MS
Regresja	1	2511,696109	2511,696
Resztkowy	24	27,38235214	1,140931
Razem	25	2539,078462
	Współczynniki	Błąd standardowy	t Stat	Dolne 95%	Górne 95%
Przecięcie	0,216	0,431346232		-0,674255	1,106254685
t	1,310495726	0,0279307		1,2528496	1,368141846

1. Model opisujący kształtowanie się wielkości produkcji systemów komputerowych w latach 1996 - 2002 ma postać:.........................................................................................

2. Zinterpretuj parametry modelu.

3. Współczynnik determinacji wynosi ..............% i oznacza, że .........................................................................

4. Oblicz wartości empiryczne statystyki t - Studenta i uzupełnij w tabeli.

5. Czy wszystkie zmienne są istotne na poziomie istotności
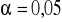
   ? (odpowiedz uzasadnij).

Zadanie 2

Na podstawie informacji z lat 1995-2003 dotyczących liczby absolwentów pewnej uczelni (w tys. osób) uzyskano:

=	506,89
	67,5
	343,5

1. Oszacuj parametry trendu liniowego i zapisz odpowiednie równanie (pierwszy wyraz wolny, drugi wsp. kierunkowy)

6. Zinterpretuj parametry modelu.

7. Współczynnik determinacji wynosi ..............% i oznacza, że ..........................................................

8. Oblicz wartości empiryczne statystyki t - Studenta i oceń, czy wszystkie zmienne są istotne na poziomie istotności
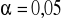
   ? (wartość krytyczna t_kr=2,364).