Laboratorium z Fizyki
Borek Rafał	Grupa 11	Wydział Mechaniczny		Politechnika Świętokrzyska		1998-03-23
Nr ćwiczenia	Wyznaczanie Modułu Younga
M10
		Ocena	Data		Podpis
Teoria
Wykonanie

WSTĘP TEORETYCZNY

Jeśli na jakieś nieruchome ciało wywierana jest pewna siła, to znaczy jeśli doznaje ono pewnego ciśnienia p, to w ciele tym występują odkształcenia, czyli deformacje. Deformacje mogą być związane ze zmianami objętości ciała, lub też ze zmianami kształtu ciała. W praktyce zwykle jeden rodzaj odkształcenia występuje obok drugiego, przy czym może się zaznaczyć wyraźna przewaga jednego z nich, co w rozważaniach przybliżonych upoważnia do zaniedbania drugiego.

Odkształcająca ciało siła zewnętrzna powoduje zmianę odległości międzycząsteczkowych. Tej zmianie przeciwstawiają się siły międzycząsteczkowe ciała, dzięki którym powstaje tzw. opór sprężysty albo siła sprężystości, siła ta jest skierowana przeciwnie względem siły odkształcającej, a co do wartości jest jej równa. Siła oporu sprężystego jest tym większa, im większe jest odkształcenie, rośnie ona liniowo wraz z odkształceniem. Ilościowo ujmuje tę zależność prawo Hooke'a, które wyraża się równaniem:

α - oznacza odkształcenie względne,

p - ciśnienie,

k - współczynnik proporcjonalności zwany modułem sprężystości, który ma dla danego materiału wartość stałą zależną od rodzaju odkształcenia.

Z chwilą gdy ustaje działanie zewnętrznej siły odkształcającej, ciało powraca do pierwotnego stanu, siły napięć sprężystych, które powstały we wnętrzu ciała, sprawiają, że cząsteczki powracają do pierwotnych położeń. Oczywiście następuje to tylko wówczas, gdy siła odkształcająca nie przekracza granicy sprężystości, w przeciwnym bowiem razie doznane odkształcenia ciała nie ustępują z chwilą zniknięcia siły zewnętrznej. Takie odkształcenia nazywamy plastycznymi. Prawo Hooke'a jest słuszne jedynie w odniesieniu do odkształceń sprężystych, a więc znikających wraz z działaniem siły zewnętrznej. Zależnie od rodzaju odkształcenia mamy dla danego materiału różne moduły sprężystości.

Odkształcenie względne wyraża się stosunkiem odkształcenia bezwzględnego do początkowych wymiarów ciała i jest wobec tego liczbą oderwaną.

Największe znaczenie praktyczne ma moduł sprężystości na wydłużenie. Nosi on nazwę modułu Younga i oznaczany jest symbolem E

Z wyrażenia tego łatwo odczytać sens fizyczny modułu Younga: jest to takie ciśnienie, które spowodowało by odkształcenie względne równe jedności (oczywiście przy nie przekraczaniu granicy sprężystości). W przypadku prostego wydłużenia

będzie równe jedności, gdy , to znaczy, gdy pręt zostanie rozciągnięty do podwójnej długości. W praktyce rzadko można osiągnąć takie odkształcenia bez przekroczenia granicy sprężystości ( wyjątek stanowi np. guma ).

WYZNACZANIE MODUŁU YOUNGA METODĄ BEZPOŚREDNIĄ

Pomiar strzałki ugięcia dokonuje się przy pomocy czujnika mikrometrycznego. Po ustawieniu belki na podporach i wstępnym, obciążeniu ustawia się czujnik tak, aby głowica pomiarowa dotykała do belki, następnie zeruje się czujnik sprawdzając kilkakrotnie czy po odciągnięciu głowicy ręka wraca ona do tej samej pozycji. W trakcie obciążania belki obciążnikami za każdym razem gdy zwiększamy obciążenie odczytujemy z czujnika wartość strzałki ugięcia.

WYZNACZANIE MODUŁU YOUNGA ZA POMOCĄ TENSOMETRU

Do wyznaczania modułu Younga metodą tensometryczną wykorzystuje się dwa tensometry oporowe typu RL 120/10 naklejone z dwu stron na belką i włączone do układu mostkowego. Jedna przekątna mostka jest zasilana napięciem stałym, a do drugiej przyłączony jest „Wskaźnik zera” za pośrednictwem potencjometrów „Zerowanie” i „Równoważenie”.

Przed dokonaniem pomiarów należy wyzerować „Wskaźnik zera”. Następnie potencjometr „Równoważenie” ustawić w pozycję (500 działek) i przy wstępnym obciążeniu belki, potencjometr „Zerowanie” zrównoważyć mostek przy maksymalnej czułości „Wskaźnika zera”. Zmiana obciążenia belki powoduje wzrost rezystancji jednego tensometru i malenie drugiego.

W metodzie tej wykorzystuje się zjawisko zmiany rezystancji cienkich drucików tensometru pod wpływem wydłużania lub skracania. Zmiana rezystancji jest wprost proporcjonalna do jednostkowego wydłużenia bądź skrócenia.

gdzie:

D - stała

K - stała tensometrów

R - rezystancja tensometru

b, h, k - wymiary belki

ΔR/R - jednostkowa zmiana rezystancji tensometru

Wykonywanie ćwiczenia

Wyniki:

Obciążenie P [N]		Strzałka ugięcia						Wskazania tensometru
				f1 [mm]		f2 [mm]		fśr [mm]		ΔR1 [Ω]		ΔR2 [Ω]		ΔRśr [Ω]
4,9		0,71		0,74		0,725		0,03		0,036		0,033
9,8		1,47		1,54		1,505		0,06		0,076		0,068
14,7		2,28		2,22		2,25		0,092		0,108		0,1
19,6		3		3,06		3,03		0,132		0,14		0,136
24,5		3,77		3,87		3,82		0,168		0,18		0,174
29,4		4,52		4,46		4,49		0,204		0,208		0,206
34,3		5,12		5,31		5,215		0,232		0,248		0,24
39,2		5,96		6,09		6,025		0,268		0,284		0,276
44,1		6,64		6,83		6,735		0,3		0,32		0,31
49		7,35		7,53		7,44		0,32		0,356		0,344

1. Parametry prostej:

n = 10

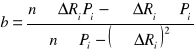
b = 141,545

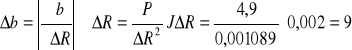
b = 141,545 ± 9

2. obliczenie modułu

E = b ⋅ D = 14037,02

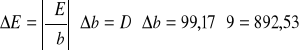
E = 14037 ± 892,53 MPa

3. Obliczanie dokładności wyznaczenia prostej z pomiarów strzałki ugięcia :

n	1	2	3	4	5	6	7	8	9	10
Yi	50,52⋅10^14	1,049⋅10^14	1,568⋅10^14	2,111⋅10^14	2,662⋅10^14	3,129⋅10^14	3,634⋅10^14	4,199⋅10^14	4,693⋅10^14	5,185⋅10^14

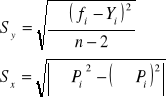
S_y = 5,196 S_x = 25,69

4. Średnie błędy kwadratowe jakimi obarczone są współczynniki a i b dla prostej wyznaczonej z pomiarów strzałki ugięcia:

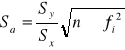
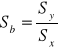
S_a = 6,275 S_b = 0,202

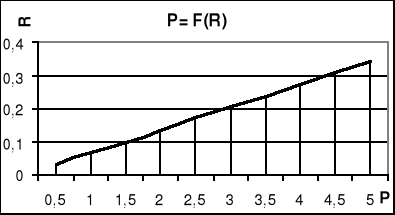
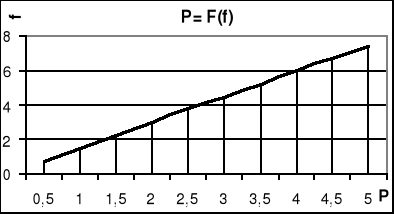
1

4

---