Ciągła zmienna losowa ma rozkład wykładniczo - potęgowy dany zależnością
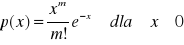
. Obliczyć jej wartość średnią i wariancję.Ciągła zmienna losowa ma rozkład dany wzorem
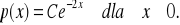
Wyznaczyć stałą C, dystrybuantę, wartość średnią, i wariancję tej zmiennej losowej.
Ciągła zmienna losowa ma rozkład dany wzorem
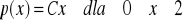
. Wyznaczyć stałą C, dystrybuantę, wartość średnią, i wariancję tej zmiennej losowej.
Ciągła zmienna losowa ma rozkład prawdopodobieństwa Couchye'go
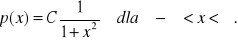
Wyznaczyć stałą C, dystrybuantę, wartość średnią, i wariancję tej zmiennej losowej.
Gęstość prawdopodobieństwa zmiennej losowej dwuwymiarowej dana jest wzorem
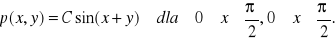
Wyznaczyć stała C, dystrybuantę, rozkłady brzegowe zmiennych losowych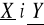
oraz ich wartości średnie, wariancje, współczynnik korelacji.
Dany jest rozkład łączny zmiennych losowych
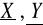
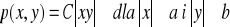
. Wyznaczyć stała C, rozkłady brzegowe zmiennych losowych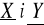
oraz ich wartości średnie, wariancje, współczynnik korelacji.
Dwuwymiarowa zmienna losowa ma rozkład prawdopodobieństwa dany wzorem
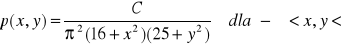
. Wyznaczyć stała C, dystrybuantę, rozkłady brzegowe zmiennych losowych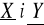
oraz ich wartości średnie, wariancje, współczynnik korelacji.
Dwuwymiarowa zmienna losowa ma rozkład prawdopodobieństwa dany wzorem
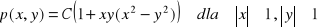
. Wyznaczyć stałą C, rozkłady brzegowe zmiennych losowych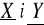
oraz ich wartości średnie, wariancje, współczynnik korelacji.
Znaleźć funkcję gęstości prawdopodobieństwa zmiennej losowej, której funkcja charakterystyczna wynosi
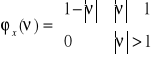
.
Funkcja charakterystyczna ciągłej zmiennej losowej ma postać
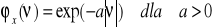
. Wyznaczyć funkcję gęstości prawdopodobieństwa tej zmiennej.
Średnia prędkość wiatru w pewnej miejscowości wynosi 16km/h. Oszacować prawdopodobieństwo tego, że w tym mieście prędkość wiatru nie przekroczy 80km/h.
Liczba słonecznych dni w roku w pewnej miejscowości jest zmienną losową o wartości średniej 75 dni. Ocenić prawdopodobieństwo tego, że w ciągu roku w miejscowości tej będzie więcej niż 200dni słonecznych.
Średnie zapotrzebowanie na energię elektryczną w ciągu miesiąca w pewnej dzielnicy Warszawy wynosi 360 tysięcy kWh. Ocenić prawdopodobieństwo tego, że zapotrzebowanie energii w maju przekroczy 1 milion kWh. Oszacować to prawdopodobieństwo wiedząc, że średnie odchylenie standardowe zapotrzebowania energii wynosi 160 tysięcy kWh.
Gaussowska zmienna losowa ma rozkład dany wzorem
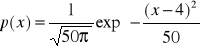
. Oszacować prawdopodobieństwo, że zmienna losowa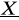
odchyli się poza wartość średnią o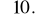
Oszacować prawdopodobieństwo, że zmienna losowa o rozkładzie
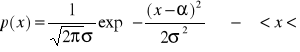
odchyli się od swojej wartości średniej o cztery odchyłki standardowe.
Wyszukiwarka
Podobne podstrony:
2048
2048
2048, Święto górnika
2048
2048
2048
Warszawa 2048 KONKURS
Kingston 2048 MB
2048 02 EN Citaro CNG
clonix RTD 2048
2048
więcej podobnych podstron