Refrakcja atmosferyczna

Zjawisko załamania promieni światła w atmosferze nazywamy refrakcją. Refrakcją atmosferyczną nazywamy zmianę obserwowanego kierunku do gwiazdy.

Różnica kierunków z i z' jest wielkością refrakcji r:

r = z - z'.

Poprawkę refrakcyjną r do pomierzonej odległości zenitalnej można wyznaczyć ze wzoru Radau:

r = R_o + R_o Aαγ + R₁ Bβ,

gdzie:

R₁ = R_o +R_o Aαγ.

Do powyższego wzoru publikowane są w Roczniku Astronomicznym specjalne tablice. R_o oznacza refrakcję normalną, której wartość określona jest dla ustalonych wartości ciśnienia, temperatury i wilgotności. Wartości te wyznaczone są w funkcji odległości zenitalnej. Pozostałe współczynniki znajduje się z tablic według funkcji następujących argumentów:

A = f(t^oC) - temperatury,

B = f(H_mmHg) - ciśnienia atmosferycznego,

α = f(z') - pomierzonej odległości zenitalnej,

β = f(R₁) - współczynnik stabelaryzowany według R₁,

γ = f(z', t) - pomierzonej odległości zenitalnej i temperatury,

Refrakcja atmosferyczna w horyzoncie (dla z = 90^o) wynosi według Radau R_h = 36' 36”.

Na skutek refrakcji czas widzialności ciała niebieskiego wydłuża się. Do wzorów na t i A dla momentów wschodu i zachodu gwiazdy należy wprowadzić następujące poprawki:

,

.

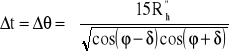
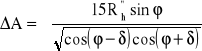
Ze względu na wielkość refrakcji, przy wszystkich wyznaczeniach astronomicznych należy szczególnie uwzględniać odpowiednie poprawki do pomierzonych odległości zenitalnych:

z = z' + R

Aberracja światła

Aberracją nazywamy zmianę kierunku widzenia ciała niebieskiego na sferze spowodowaną ruchem obserwatora.

Obserwator znajdujący się w punkcie A bierze udział wraz z Ziemią w kilku jednocześnie odbywających się ruchach:

• w ruchu obrotowym Ziemi, powodującym aberrację dobową,

• w ruchu obiegowym Ziemi wokół Słońca - aberracja roczna,

• w ruchu Słońca wraz z Układem Słonecznym wokół centrum Galaktyki - aberracja wiekowa.

Promienie światła rozchodzą się od gwiazdy G z prędkością światła c. Obserwator A wraz z Ziemią ma prędkość v. Wartość kąta υ, o który obserwator musi pochylić lunetę, oblicza się z zależności:

, skąd:

.

Wartość aberracji dobowej można obliczyć podstawiając do powyższego wzoru prędkość obserwatora wynikającą z ruchu obrotowego Ziemi. Prędkość obrotową Ziemi na szerokości geocentrycznej φ' wyraża się wzorem:

.

Podstawiając do dwóch powyższych wzorów następujące wartości: R = 6371 km, c = 2,998 · 10⁵ km/s, otrzymamy:

v = 0,464 cos φ' [km/s], oraz:

υ" = 0,319”cos φ' sin w.

Przyjmując: φ' = φ, otrzymamy:

υ" = k cos φ sin w,

gdzie: k = 0,319” = 0,021^s - stała aberracja dobowa.

Przyjmując, że orbita Ziemi jest kołowa, można wyznaczyć aberrację roczną κ = 20,496”.

3

---