Weryfikacja hipotez statystycznych

1. Wnioskowanie statystyczne - w jakim celu?

2. Weryfikacja hipotez statystycznych - dla jakich wartości - parametrów zmiennej.

3. Oznaczenia: H0 i H1, statystyka testu, test statystyczny, błędy I i II rodzaju

4. Etapy postępowania: określenie problemu i cel testu, budowa H0 i H1, wybór i obliczenie statystyki, konstrukcja obszaru krytycznego, decyzja o przyjęciu lub odrzuceniu H0.

Test hipotetycznej średniej w populacji

o rozkładzie normalnym

dla n < 30,

odchylenie standardowe w populacji nieznane

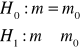
test dwustronny

albo

testy jednostronne

test prawostronny

lub

test lewostronny

Statystyka testu ma postać:

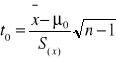
- średnia z próby

- odchylenie standardowe z próby

- testowana średnia populacji

- liczebność próby

Test dwustronny

odczytujemy z tablic t-Studenta wartość krytyczną t_α,n-1

Jeżeli
, (
) odrzucamy

Jeżeli
, nie ma podstaw do odrzucenia

Test jednostronny

lub

odczytujemy z tablic t-Studenta wartość krytyczną t_2α,n-1

dla
i

Jeżeli
, istnieją podstawy do odrzucenia

Jeżeli
, nie ma podstaw do odrzucenia

dla
i

Jeżeli
, istnieją podstawy do odrzucenia

Jeżeli
, to nie ma podstaw do odrzucenia

α - ustalony z góry poziom istotności

gdy:

1.
oraz nieznane odchylenie standardowe

2. odchylenie standardowe populacji
znane

stosujemy statystykę U o rozkładzie normalnym

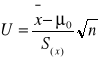
Z tablic rozkładu normalnego odczytujemy wartości krytyczne:

dla testu dwustronnego
- odczytujemy wartość
taką, że

dla testu jednostronnego lewostronnego

- odczytujemy wartość
taką, że

dla testu jednostronnego prawostronnego

- odczytujemy wartość
taką, że

Test dla średniej w dwóch populacjach

1. Znane odchylenie standardowe w obu populacjach o różnych liczebnościach i rozkładzie normalnym

Statystyka Z ma rozkład normalny

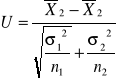
Wartość krytyczną
odczytujemy z tablic dystrybuanty rozkładu normalnego - odpowiednio dla testu dwustronnego, jednostronnego (jak w teście dla średniej w jednej populacji)

2. Odchylenie w populacji nieznane ale równe, duża próba

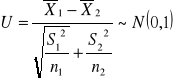
Wartość krytyczną
odczytujemy z tablic dystrybuanty rozkładu normalnego - odpowiednio dla testu dwustronnego, jednostronnego (jak w teście dla średniej w jednej populacji)

3. Odchylenia standardowe w populacjach nie znane, ale równe, mała próba (n1+n2 < 120), populacje mają rozkład normalny

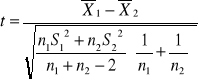
Wartość krytyczną odczytujemy z tablic rozkładu t-Studenta dla α i n₁+n₂-2 stopni swobody (test dwustronny) lub dla 2α i n₁+n₂-2 stopni swobody (testy jednostronne)

---