Wstęp teoretyczny

Prawa Ohma dla obwodu zamkniętego ma postać:

ε=IR

,gdzie ε oznacza siłę elektromotoryczną.

Jeżeli obwód składa się ze źródła prądu o sile elektromotorycznej ε, oporu wewnętrznego r oraz z części zewnętrznej o oporze R. W takim przypadku mamy:

U=IR

, gdzie

I =
.

Stąd

U=

Prawa Kirchoffa opisują przepływ prądu w złożonych obwodach:

Pierwsze prawo mówi, że suma algebraiczna natężeń prądów schodzących się w węźle równa się zeru.

Drugie natomiast brzmi: W dowolnym obwodzie zamkniętym, wydzielonym w rozgałęzionej sieci elektrycznej, suma algebraiczna iloczynów natężeń prądowi oporów poszczególnych odcinków tego obwodu równa się sumie algebraicznej działających w nim sił elektromotorycznych.

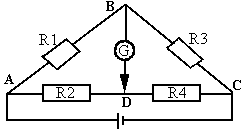
Mostek Wheatstone'a:

W tak zbudowanym mostku prąd nie płynie przez galwanometr jedynie wtedy, gdy

Jest tak ponieważ w takim przypadku różnica potencjałów między punktami b i d jest równa zeru. Udowodnić to możemy korzystając najpierw z prawa Ohma i zapisując

U=IR.

Stąd

I₁R₁=I₂R₂ oraz I₃R₃=I₄R₄.

Ponieważ przez mostek CD nie płynie prąd to z I prawa Kirchoffa mamy

I₂=I₄ oraz I₁=I₃.

Uwzględniając to otrzymujemy naszą proporcję.

L₁/L₂=R₁/R₂

Opór zabezpieczający jak sama jego nazwa wskazuje służy do zabezpieczenia galwanometru przed uszkodzeniem przez zbyt duży prąd.

Jeżeli mamy opory połączone równolegle to odwrotność oporu zastępczego jest równa sumie odwrotności poszczególnych oporów. Natomiast przy połączeniu równoległym oporów opór zastępczy równy jest sumie poszczególnych oporów.

Minimalny błąd:

Dokładność opornicy dekadowej jest stała i nie odgrywa roli w naszym rozwiązaniu. Ponieważ błąd:

A więc można przyjąć, że;

Co daje:Przebieg doświadczenia

Po zmontowaniu układu pomiarowego zgodnie ze schematem zawartym we wstępie do ćwiczenia, przystępujemy do pomiarów.

Pomiary dokonujemy dla kilku oporów oraz dla trzech odległości L₁ (1/3L; 1/5L; 2/3L). Czynności powtarzamy dla różnych ustawień oporu zabespieczającego.

Opracowanie wyników

Uśrednienie wyników:

R₁:

R_L/3=(112+106,1+106+105,9+105,5+105)/7=106,64 [Ω]

R_L/2=(58+53,6+53,4+54,5+54+54,3+54,1)7=54,56 [Ω]

R_2L/3=(30,2+27,1+27,2+27,4+27,3+27,3+27,4)=27,7 [Ω]

R₃:

R_L/3=(891,2+891,4+892+892,5+897,2+898,1+897,4)/7=894,27 [Ω]

R_L/2=(450,1+451+450,5+450,2+450+449,6+449,2)/7=450,09 [Ω]

R_2L/3=(230,1+230,6+230,3+230,2+231+230,7+230,1)/7=230,43 [Ω]

R₅:

R_L/3=(6600+6610+6590+6605+6625+6640+6650)/7=6617,14 [Ω]

R_L/2=(3180+3170+3160+3170+3185+3200+3180)/7=3177,86 [Ω]

R_2L/3=(1580+1585+1590+1580+1585+1601+1600)/7=1588,71 [Ω]

R₃+R₅:

R_L/3=(7200+7201+7202+7250+73600+7400+7400)/7=7279 [Ω]

R_L/5=(3600+3620+3640+3630+3620+3650+3670)/7=3632,86 [Ω]

R_2L/3=(1820+1805+1810+1820+1830+1825+1820)/7=1818,57 [Ω]

Wartości oporów:

Przykładowe obliczenia:

Dla L₁=L/3

Rx = R/2

Wartości dla R₁ Rx = 106,64/2 = 53,32 [Ω]

Wartości dla R₂ Rx = 894,27/2 = 447,14 [Ω]

Wartości dla R₃ Rx = 6617,14/2 = 3 308,57 [Ω]

Wartości dla R₃+R₅ Rx = 7279,00/2 = 3 639,50 [Ω]

Dla L₁=L/2

Rx = R

Wartości dla R₁ Rx = 54,56 [Ω]

Wartości dla R₂ Rx = 450,09 [Ω]

Wartości dla R₃ Rx = 3 177,86 [Ω]

Wartości dla R₃+R₅ Rx = 3 632,86 [Ω]

Dla L₁=2L/3

Rx = 2R

Wartości dla R₁ Rx =2*27,70= 55,40 [Ω]

Wartości dla R₂ Rx =2*230,43=460,86 [Ω]

Wartości dla R₃ Rx =2*1588,71=3 177,43 [Ω]

Wartości dla R₃+R₅ Rx =2*1818,57= 3 637,14 [Ω]

Otrzymane wyniki :

Pomiar dla:	L1=L/3	L1=L/2	L1=2L/3	Rśr[Ω]
R1 [Ω]	53,32	54,56	55,40	54,43
R3 [Ω]	447,14	450,09	460,86	452,69
R5 [Ω]	3 308,57	3 177,86	3 177,43	3 221,29
R3+R5 [Ω]	3 639,50	3 632,86	3 637,14	3 636,50

Ocena błędów:

∆R=1000*0,05%+100,05%+10*0,05%+1*0,1% [Ω]

Pomiar dla:	L1=L/3	L1=L/2	L1=2L/3	∆Rśr[Ω]
∆R1 [Ω]	0,03	0,03	0,03	0,03
∆R3 [Ω]	0,23	0,23	0,23	0,23
∆R5 [Ω]	1,61	1,59	1,59	1,60
∆R3+∆R5 [Ω]	1,82	1,82	1,82	1,82

Wnioski:

---