Paweł Kiraga

Całkowanie numeryczne - metoda prostokątów

W metodzie prostokątów korzystamy z definicji całki oznaczonej Riemanna , w której wartość całki interpretowana jest jako suma pól obszarów pod wykresem krzywej w zadanym przedziale całkowania <x_p,x_k>. Sumę tę przybliżamy przy pomocy sumy pól odpowiednio dobranych prostokątów. Sposób postępowania jest następujący:

Przedział całkowania <x_p,x_k>. dzielimy na n równo odległych punktów x₁,x₂,...,x_n. Punkty te wyznaczamy w prosty sposób wg wzoru:

dla i = 1,2,...,n

Obliczamy odległość między dwoma sąsiednimi punktami - będzie to podstawa każdego prostokąta:

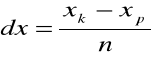
Dla każdego wyznaczonego w ten sposób punktu obliczamy wartość funkcji f(x) w tym punkcie:

f_i = f(x_i), dla i = 1,2,...,n

Obliczamy sumę iloczynów wyznaczonych wartości funkcji przez odległość dx między dwoma sąsiednimi punktami - da to sumę pól poszczególnych prostokątów ograniczonych wykresem funkcji:

S = f₁ dx + f₂ dx + ... + f_n dx

a po wyprowadzeniu wspólnego czynnika przed nawias:

S = dx (f₁ + f₂ + ... + f_n)

Otrzymana suma jest przybliżoną wartością całki oznaczonej funkcji f(x) w przedziale <x_p,x_k>.

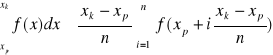
Przykład:

Obliczymy ręcznie przybliżoną wartość całki oznaczonej z funkcji f(x) = sin(x) w przedziale <0,π>.

Przedział podzielimy na n = 4 punkty:

Odległość między dwoma sąsiednimi punktami wynosi:

Dla każdego z wyznaczonych punktów obliczamy wartość funkcji f(x) = sin(x):

Obliczamy sumę pól prostokątów:

S = dx (f₁ + f₂ + f₃ + f₄)

S = 0,7854 (0,7071 + 1,000 + 0,7071 + 0,0000)

S = 0,7854 * 2,4142

S = 1,8961

Dokładna wartość takiej całki oznaczonej wynosi wg tablic:

Całkowanie numeryczne - metoda trapezów

Opisana w poprzednim rozdziale metoda prostokątów nie jest zbyt dokładna, ponieważ pola użytych w niej prostokątów źle odwzorowują pole pod krzywą. Dużo lepszym rozwiązaniem jest zastosowanie zamiast nich trapezów o wysokości dx i podstawach równych odpowiednio wartości funkcji w punktach krańcowych.. Sama zasada nie zmienia się.

Przedział całkowania <x_p,x_k>. dzielimy na n+1 równo odległych punktów x₀,x₁,x₂,...,x_n. Punkty te wyznaczamy w prosty sposób wg wzoru:

dla i = 0,1,2,...,n

Obliczamy odległość między dwoma sąsiednimi punktami - będzie to wysokość każdego trapezu:

Dla każdego wyznaczonego w ten sposób punktu obliczamy wartość funkcji f(x) w tym punkcie:

dla i = 0,1,2,...,n

f_i = f(x_i)

Pole pod wykresem funkcji przybliżane jest polami n trapezów. Pole i-tego trapezu obliczamy wg wzoru:

dla i=1,2,...,n

Przybliżona wartość całki jest sumą pól wszystkich otrzymanych w ten sposób trapezów:

s = P₁ + P₂ + ... + P_n

czyli

Wyprowadzony na końcu wzór jest podstawą przybliżonego wyliczania całki w metodzie trapezów.

Przykład:

Obliczymy ręcznie przybliżoną wartość całki oznaczonej z funkcji f(x) = sin(x) w przedziale <0,π>.

Przedział podzielimy na n+1 = 5 punktów:

Odległość między dwoma sąsiednimi punktami wynosi:

Dla każdego z wyznaczonych punktów obliczamy wartość funkcji f(x) = sin(x):

f_o = f (x_o) = sin 0 = 0,0000

Obliczamy sumę pól trapezów:

s = 0,7854(0.7071+1+0.7071) = 1,8961

---