I.

1. Różniczkowe równanie falowe. Pokazać, że ukryta jest w nim dynamika ruchu falowego.

 (x,y) jest to funkcja dwóch współrzednych, świadczy to o tym, że energia rozchodzi się na sposób falowy. Rówanie falowe w dowolnej chwili czasu =Asin(wt-kx); Y=Asin2pi/T*(t-x/r); Równamie różniczkowe fali: d2y/dx2=(1/v*v)*(d2y/dt2). Z II-ej zasady dynamiki

1) dF/dx=*s*d2y/dt2 2) dy/dr= F/E*S

mamy : d2Y/dx2=1/ES*dE/dx => E*S*d2Y/dx2= dF/dx p

2. Wahadło matematyczne i fizyczne w kontekście ruchu harmonicznego

Współczynnik proporcjonalności między siłą sprężystą i wychyleniem ciężarka z położenia równowagi , K=K_wS/l_p liczbowo równy sile wywołującej wydłużenie sprężyny o jednostkę długości, nazywać będziemy współczynnikiem sprężystości sprężyny. F_S=-k*x - siła sprężystości jest wprost proporcjonalna do wydłużenia ciała i jest przeciwnie do tego wydłużenia zwrócona. Dynamiczne równanie ruchu ma postać : -k*x=m*a, x- wychylenie ciała z położenia równowagi, a=-(k/m)*x. Stąd okres drgań : _(k/m)^1/2, T=2_

Wahadłem matematycznym nazywamy punkt materialny zawieszony na długiej nierozciągliwej i nieważkiej nitce. Siłę ciężkości działającą na ten punkt rozkładamy na dwie składowe - równoległą i prostopadłą do nitki. Składowa prostopadła jest bezpośrednią przyczyną drgań tego wahadła. Drgania wahadła są wywołane przez siłę proporcjonalną do wychylenia i przeciwnie do tego wychylenia zwróconą. Dla małych kątów  odległość x jest równa wychyleniu wahadła z położenia równowagi, a zatem okres drgań tego wahadła jest zgodna ze wzorem T=2(l/g)^1/2.

Wahadłem fizycznym nazywamy bryłę sztywną wahającą się wokół osi obrotu nie przechodzącą przez środek jej masy. Dynamiczne równanie ruchu ma postać -m*g*r*sin(=I_E, dla małych kątów równanie piszemy w postaci m*g*r*=I_E Okres drgań wahadła fizycznego wynosi T=(I/m*g*r)^1/2. Jak widać na okres drgań wahadła fizycznego mają wpływ moment bezwładności bryły względem osi obrotu oraz odległość środka masy tej bryły od osi obrotu

3. RÓWNANIE MAXWELLA:

Maxwell traktował przestrzeń jako ośrodek materialny - eter. Jeśli w przestrzeni nie ma żadnej dotykalnej materii, prąd przesunięcia płynie w jakimś ośrodku.

Postać całkowa równań Maxwella:

Postać różniczkowa równań Maxwella:

L	dowolna krzywa zamknięta
S	dowolna powierzchnia zamknięta
Q	całkowity ładunek elektryczny
	Wektor indukcji magnetycznej
	Wektor natężenia pola elektrostatycznego
μ0	Przenikalność magnetyczna próżni
	Przenikalność elektryczna próżni
ΦE	Strumień natężenia pola elektrycznego
ΦB	Strumień natężenia pola magnetycznego
	Gęstość prądu elektrycznego w danym punkcie
ρ	Gęstość ładunku w danym punkcie

Są to cztery sprzężone równania różniczkowe cząstkowe .Stosują się one do każdego punktu przestrzeni pola elektromagnetycznego. W próżni gęstość ładunku ρ oraz prądu I równa się zero.

Maxwell jako pierwszy zasugerował, że światło jest falą elektromagnetyczną o określonym zakresie częstotliwości.

II.

1. Scharakteryzuj ruch precyzyjny na podstawie bąka i żyroskopu.

PRECESJA - zjawisko towarzyszące ruchowi obrotowemu bryły sztywnej wokół zamocowanego punktu lub wokół środka masy. Jeśli ruch taki da się rozłożyć na dwa następujące obroty składowe:

1. obrót bryły ze stałą co do wartości bezwzględnej prędkością kątową wokół osi związanej sztywno z bryłą

2. obrót osi związanej z bryłą ze stałą prędkością kątową wokół osi nieruchomej względem układu odniesienia to ten drugi obrót nazywa się PRECESJĄ

BĄK - Badając bąka symetrycznego odnajdujemy 2 przypadki precesji.

1. występuje jeżeli względem punktu  który jest punktem zamocowania lub średniej masy, moment sił zewnętrznych działających na bąk symetrii równy jest  (np.: gdy jedna siła zewnętrzna jest siłą ciężkości, a pkt. wokół którego bąk się obraca jest jego środkiem ciężkości. Pkt. Ten może być środkiem masy bąka unoszącego się swobodnie w przestrzeni. Oś symetrii takiego bąka pozbawiona momentu sił zewnętrznych, obraca się na ogół ze stałą prędkością kątową wokół nieruchomej osi mającej kierunek wektora momentu pędu bąka czyli wykonuje PRECESJE. Nie było by Precesji w przypadku gdy bąk został wprowadzony w ruch obrotowy dokładnie wokół osi symetrii lub osi do niej prostopadłej. Osie te jako główne osie bezwładności zachowałyby stały kierunek w przestrzeni.

2. Występuje np. wtedy gdy na bąk działa siła ciężkości, a unieruchomiony jest pkt. Różny od środka ciężkości np. (zabawka stojąca ostrą nóżką na szorstkiej powierzchni po której nie może się ślizgać). Występujący względem pkt. zamocowanego moment siły ciężkości powoduje że wektor momentu pędu bąka nie jest stały lecz obraca się jednostajnie wokół osi planowej. Obraca się również jednostajnie wokół niej oś symetrii bąka mamy więc wymuszoną Precesje.

ŻYROSKOP - bąk symetrii - bryła sztywna zawieszona w taki sposób że 1 z pkt. osi symetrii obrotowej zajmuje stałe położenie w przestrzeni a ponadto istnieje możliwość wprowadzenia tej bryły w szybki ruch obrotowy wokół tej osi. Żyroskop w zawieszeniu Cardona; pkt. nieruchomym jest środek masy i żyroskop jest bąkiem swobodnym to jest o 3 stopniach swobody. Na ogół żyroskop jest zbudowany w taki sposób, że jego oś obrotu jest osią swobodną i stałą tzn. o największym momencie bezwładności. Żyroskop pozostający w spoczynku reaguje na przyłożony moment siły obracając się w kierunku zgodnym z przyłożonym momentem siły. W przypadku gdy żyroskop jest wprowadzony w szybki ruch obrotowy, kierunek osi żyroskopu jest wówczas zarazem kierunkiem jego momentu pędu i aby zmienić położenie tej osi trzeba położyć moment siły powodując odpowiednią zmianę momentu pędu. Przyłożenie pary sił o momencie D sprawi że w ciągu krótkiego czasu t moment pędu I zwiększy się o I = t*D a oś obrotu obróci się wokół pionowej osi przyjmując położenie równoległe do zmienionego wektora momentu pędu I+I. Jeżeli przy tym moment siły D będzie stale prostopadły do osi Żyroskopu. Zachowując stałą wartość bezwzględną, oś żyroskopu będzie obracać się w płaszczyźnie poziomej. Taki ruch jest przykładem ruchu precesyjnego.

3. Całki ruchu

W układach zamkniętych (nie ma tam sił zewn.) istnieją takie funkcje współrzędnych i prędkości cząstek tworzących układ, które zachowują stałą wartość podczas możliwych ruchów układu. Funkcje te nazywamy całkami ruchu. Dla układu złożonego z N cząstek, między którymi nie ma sztywnych wiązań, można utworzyć 6N-1 całek ruchu. My jednak zajmiemy się całkami i własnościach addytywności. Polega ona na tym (addytywność) ze wartości całki ruchu dla układu złożonego z podukładów nie oddziałujących między sobą jest równa sumie wartości tej całki ruchu dla poszczególnych podukładow. Są 3 addytywne całki ruchu: energia, pęd i moment pędu. W związku z tym w układach zamknietych spełnione są 3 zasady zachowania: energii, pędu i momentu pędu. Są one ścisle związane z podstawowymi własnościami przestrzeni i czasu. U podstaw zachowania energii leży jednorodność czasu, tzn. równouprawnienie wszystkich chwil czasu. Należy to rozumieć następująco: zastąpienie chwili T1 chwilą T2 bez zmiany wartości współrzędnych i prędkości cząstek nie zmienia mechanicznych własności układu. Zachowanie pędu wiąże się z jednorodnością przestrzeni, tzn. z jednakowymi własnościami przestrzeni we wszystkich punktach. Należy to rozumieć w tym sensie, że równoległe przeniesienie układu zamknietego z jednego miejsca przestrzeni do drugiego, bez zmiany wzajemnych położeń cząstek, nie wpływa na mechaniczne własności układu (jeżeli układ na nowym miejscu jest nadal zamknięty). Zachowanie mom. Pedu wiąże się z izotropowością przestrzeni, tzn. jednakowymi własnościami przestrzeni we wszystkich kierunkach. Oznacza to, że obrót układu zamkniętego jako całości nie wpływa na mechaniczne włąsności tego układu.

Zasada zachowania pędu:

Twierdzenie o pędzie całkowitym - pochodna pędu całkowitego układu względem czasu jset równa wypadkowej sił zewnętrznych działających na układ: F_Z = dp/dt.

Zasadza zachowania pędu - jeżeli wypadkowa sił zew. Działających na układ punktów materialnych jest równa zeru, to pęd całkowity tego układu jest stały: F_Z= 0 => p=const. Albo - jeżeli wypadkowa sił wew. Działających na układ jest równa zeru , to pęd układu w stanie początkowym jest równy pędowi układu w stanie końcowym.

Zasada zachowania momentu pędu (krętu):

Kręt:
. Pochodna krętu jest równa mom. Siły:
.

Twierdzenie o kręcie całkowitym: Pochodna krętu całkowitego układu względem czasu jest równa momentowi wypadkowemu sił zewnętrznych: M_Z = dL/dt.

Zasad zach. Krętu - jeżeli moment wypadkowy sił zewnętrznych działających na układ równa się zeru, to całkowity kręt tego układu jest stały: Mz=0 => L=const;
; jeżeli prędkości kątowe poszczególnych brył są sobie równe, to:
.

Zasada zachowania energii mechanicznej - energia układu odosobnionego i zachowawczego jest stała. E_K+E_P=const.

Zasada zachowania energii - całkowita energia układu odosobnionego jest wielkością stałą. W układzie odosobnionym mogą więc zachodzić tylko przemiany jendych form energii w inne.

III

1. Prawa ruchu. Układy inercjalne i nieinercjalne.

Nie ma bezwzględnego ruchu i bezwzględnego spoczynku. Każdy ruch i spoczynek jest względny. Ciała rozpatrywane poruszają się z V<<c, niesk.=const przy przejściu z jednego układu do drugiego.

Inercjalny: Każdy układ, w którym spełniona jest I zasada dynamiki Newtona (układ, który spoczywa lub porusza się ruchem jednostajnym) nieinercjalny: Układ poruszający się z przyspieszeniem różnym od 0. Podstawowymi równaniami opisującymi ruch są r-nia Newtona (zas. Dynamiki). Przy opisie ruchu szczególnie ważną rolę odgrywa układ odniesienia; przy przejściu od układu inercjalnego do nieinercjalnego na ogół występują dodatkowe przyspieszenia (np. przyspieszenie Coriolisa). Przyspieszenie Coriolisa: dodatkowe przyspieszenie, które uzyskuje w układzie unoszenia poruszającej się względem niego ciała, dzięki ruchowi obrotowemu tego układu. Przyspieszenie Coriolisa jest równe: a_c(wektor)=2((wektor)V_(wektor)); - prędkość kątowa układu odniesienia, nieinercjalnego, względem układu inercjalnego. V_- prędkość ciała względem układu odniesienia.

2. Wg mnie jest to to samo co punkt I.1.

3. Oscylator harmoniczny

to każdy układ fizyczny, który "krąży wokół położenia równowagi z pewną ustaloną częstością". Wśród popularnych przykładów oscylatora harmonicznego podaje się wahadło, ciężarek zawieszony na sprężynce, czy też układ RLC.

Model oscylatora harmonicznego jest jednym z kilku podstawowych w całej fizyce i pojawia się niemal we wszystkich działach tej nauki.

Ściśla definicja jednowymiarowego oscylatora harmonicznego mówi, że jest to każdy układ fizyczny, którego zachowanie można opisać równaniem różniczkowym drugiego rzędu, zwanym równaniem oscylatora harmonicznego:

(1)

gdzie:

x jest wpółrzędną (np. w przypadku wahadła lub ciężarka może to być wychylenie)

&omega_o nazywa się częstością własną oscylatora (jej znaczenie fizyczne wyjaśni się poniżej)

Model opisywany powyższym równaniem nazywa się też czasem prostym oscylatorem harmonicznym.

Rozważmy przykład ciężarka wiszącego na sprężynie. Drugie prawo Newtona w połączeniu z prawem Hooke'a pozwala nam napisać równanie opisujące zachowanie ciężarka:

ma = -kx (2)

gdzie x jest wychyleniem ciężarka z położenia równowagi, a - przyspieszeniem ciężarka, m - jego masą, a k - stałą sprężystości sprężyny.

Ponieważ przyspieszenie, z definicji, jest drugą pochodną położenia po czasie, to powyższe równanie można przekształcić do postaci równania oscylatora harmonicznego, gdzie

(3)

Najprostszy sposób rozwiązania równania oscylatora polega na spostrzeżeniu, że gdy d²z/dt² ∝ -z, to z jest funkcją trygonometryczną sinus, cosinus lub ich kombinacją liniową. I tak podstawia się na próbę:

x = Acos(ωt + φ) (4)

gdzie A jest amplitudą, φ jest przesunięciem fazy, a ω jest częstością kołową. Wtedy

(5)

a po podstawieniu obu wyrażeń (4) i (5)do równania (1) otrzymujemy

(6)

Nietrywialne rozwiązanie otrzymamy tylko gdy:

(7)

Z kolei jedynym sensownym z fizycznego punktu widzenia rozwiązaniem tego równania jest

ω = ω₀ (8)

Stąd wynika bardzo istotny fakt: częstość kołowa drgań oscylatora zależy tylko od fizycznych parametrów charakteryzujących modelowany układ, a nie zależy od warunków początkowych (tj. ani od amplitudy drgań A, ani od ich początkowej fazy φ).

[Edytuj]

Oscylator harmoniczny z tłumieniem i oscylacyjną siłą wzbudzającą

W rzeczywistości przedstawiony powyżej model jest sytuacją bardzo wyidealizowaną, gdyż w każdym układzie fizycznym występują siły tarcia, oporu lub innego rodzaju tłumienie. By im przeciwdziałać oscylator pobudza się do drgań, np. za pomocą siły o charakterze oscylacyjnym. Taką bardzo często spotykaną sytuację opisuje równanie

gdzie:

&omega jest częstością drgań wymuszających

A - amplitudą drgań wymuszających

b - współczynnikiem tłumienia

W przypadku gdy A = 0, otrzymamy tzw. równanie oscylatora harmonicznego z tłumieniem, a gdy dodatkowo założymy że b = 0, oczywiście równanie prostego oscylatora.

ENERGIA W RUCHU HARMONICZNYM.

Można wyrazić energie w ruchu harmonicznym w następujący sposób (przy założeniu ze (0= 0)
. Ciało znajduje się w położeniu równowagi w chwili t=0 i t1=T/2, gdzie T jest okresem drgania. Energia kinetyczna w chwili t=0 jest równa
. Po upływie polowy okresu ciało znajduje się ponownie w położeniu równowagi, a jego energia to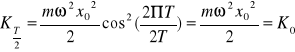
Siły sprężystości są siłami zachowawczymi. Wzór na energie potencjalna w ruchu harmonicznym V=
k(x)^2, U=
k(x₀)^2sin^2. Całkowita energia mechaniczna w ruchu harmonicznym
.Energia mechaniczna w ruchu harmonicznym jest proporcjonalna do kwadratu amplitudy tego ruchu. Energia mechaniczna jest proporcjonalna do kwadratu częstotliwości tego ruchu.

IV

1. POLE POTENCJALNE SIŁ. ENERGIA W POLU POTENCJALNYM. PRACA SIŁ POTENCJALNYCH.

Pole nazywamy potencjalnym, jeżeli można je opisać za pomocą funkcji  (x, y, z, t), której gradient określa silę w każdym punkcie pola: F = V. Funkcję H nazywamy potencjałem. Jeżeli potencjał nie zależy jawnie od czasu, tzn.  =  (x, y, z), to pole potencjalne jest stacjonarne, a jego siły są siłami zachowawczymi. Jeżeli pole jest niestacjonarne, to nie można utożsamiać sił potencjalnych i zachowawczych, chociaż pole ma potencjał  (x, y, z). Pole sił zachowawczych jest szczególnym przypadkiem potencjalnego pola sił.

Gdy praca sił pola nie zależy od drogi, lecz tylko od położeń początko­wego i końcowego, wtedy każdemu punktowi pola można przypisać wartość pewnej funkcji (x, y, z), taką że różnica wartości tej funkcji w punktach l i 2 jest równa pracy sił pola: A₁₂=U₁-U₂

Można postąpić w następujący sposób. Pewnemu punktowi O przypisujemy dowolną wartość U₀ tej funkcji. Każdemu innemu punktowi P przypisu­jemy wartość określoną wzorem U (P) = U₀+A_P0, gdzie A_P0 jest pracą wykonaną przez pole zachowawcze przy przemiesz­czaniu cząstki z punktu P do punktu 0. Ponieważ praca nie zależy od drogi, więc określona w ten sposób wartość U (P) jest wybrana jedno­znacznie. Zauważmy, że funkcja U (P) ma wymiar pracy. Zgodnie z wartości funkcji w punktach 1 i 2 wynoszą U₁ = U₀+A₁₀; U₂ = U₀+A₂₀. Obliczamy różnicę tych wartości, wiedząąc, że A₂₀ = —A₀₂. W wyniku tego otrzymujemy U₁-U₂=A₁₀-A₂₀=A₁₀+A₀₂. Suma A₁₀+A₀₂ jest pracą wykonaną przez pole przy przesuwaniu cząstki z punktu l do punktu 2 po torze przechodzącym przez 0. Jednak praca wykonana nad cząstką na drodze z punktu l do punktu 2 po dowolnym torze (niekoniecznie przechodzącym przez 0) jest jednakowa. Dlatego sumę A₁₀+A₀₂ można oznaczyć jednym symbolem A_n. Widzimy, że za pomocą funkcji U można obliczać pracę wykonaną przez siły zachowawcze na dowolnej drodze, łączącej punkty l i 2. Załóżmy, że na cząstkę działają tylko siły zachowawcze. Praca wyko­nana nad cząstką na drodze 1-2 może być przedstawiona wzorem A₁₂=U₁-U₂. Zgodnie z A₁₂=T₂-T₁, praca ta jest zużywana na wzrost energii kinetycznej cząstki. Mamy zatem wzór T2-T₁=U₁-U₂ z którego wynika, że T₂+U₂=T₁+U₁. Otrzymany wynik oznacza, że wielkość E=T+U, obliczona dla cząstki w polu sił zachowawczych, jest stała, czyli jest całką ruchu.

Z tego wynika, że U jest składnikiem całki ruchu o wymiarze energii. W związku z tym U (x, y, z) nazywamy energią potencjalną cząstki w zew­nętrznym polu sił. Wielkość E, równą sumie energii kinetycznej i energii potencjalnej, nazywamy całkowitą energią mechaniczną cząstki.

3. Twierdzenie o osiach równoległych (Schteinera).

Moment bezwładności I₀ bryły względem osi obrotu nie przechodzącej przez środek masy tej bryły jest równy sumie momentów bezwładności, I_s bryły względem osi przechodzącej przez jej środek masy oraz momentu bezwładności m(OS)² środka masy tej bryły względem osi obrotu. I­₀=I_s+m(OS)² ; m - masa bryły; OS odległość środka masy bryły od osi obrotu.

Prawo Steinera można sprawdzić na przykładie pręta

V

1****. Promieniowanie elektromagnetyczne (fala elektromagnetyczna) rozchodzące się w przestrzeni zaburzenie pola elektromagnetycznego, zaburzenie to ma charakter fali poprzecznej w której składowa elektryczna i magnetyczna prostopadłe do siebie i kierunku ruchu, nawzajem się przekształcają. Zmieniające się pole elektryczne wytwarza pole magnetyczne, a zmieniające się pole magnetyczne wytwarza pole elektryczne. Źródłem pola EM jest drgający lub przyspieszany ładunek elektryczny. Promieniowanie elektromagnetyczne rozchodząc się objawia swe własności falowe zachowując się jak każda fala, ulega interferencji, dyfrakcji, spełnia prawo odbicia i załamania.

Rozchodzenie się fali w ośrodkach silnie zależy od ośrodków oraz częstotliwości fali. Fala rozchodząc się w ośrodku pobudza do drgań cząsteczki, atomy i elektrony zawarte w ośrodku, które są źródłami fal wtórnych, zmieniając tym samym warunki rozchodzenia się fali w stosunku do próżni.

Powstawanie i pochłanianie promieniowania elektromagnetycznego wiąże się ze zmianą ruchu ładunku elektrycznego.

Własności promieniowania elektromagnetycznego silnie zależą od długości fali (częstotliwości promieniowania) i dlatego dokonano podziału promieniowania elektromagnetycznego ze względu na jego częstotliwość.

2. Fale elektromagnetyczne

Fale elektrom. rozchodzi się w próżni lub w ośrodku materialnym i jest wywołana zmianami rozkładu przestrzennego ładunków elektrycznych, objawiając się jako zmiany natężenia pól: elektrycznegoE i magnetycznegoB. Polega ona na podtrzymywaniu się nawzajem tych pól. Wynika to z praw Maxwella: K_E= -d_B/dt i K_B=₀I+₀₀ d_E/dt Załóżmy, że powstaje pole magnetyczne, jako że wcześniej nie było tego pola to zmianom pola magnetycznego towarzyszy powstanie pola elektrycznego. Jeżeli zmiany pola mag nie są jednostajne to również pole elektr. się zmienia i jest z kolei źródłem pola magnet. Takie podtrzymujące się nawzajem pola mag i elektr nazywamy falą elektromagnetyczną. Prędkość fal elektrom. zależy od właściwości elektrycznych i magnet. ośrodka: v=1/  Fale o różnych częstot rozchodzą się z różną prędkością (jedynie w próżni prędkość jest stała dla różnych częstot v  c) Fale elektrom. mogą ze sobą interferować, uginać (jeśli są spełnione warunki dyfrakcji). Jako fale poprzeczne mogą być polaryzowane.

Światło jako fala elektromagnetyczna

• Światło, tak jak promieniowanie elektromagnetyczne jest falą poprzeczną, tzn. kierunki drgań wektorów pól elektrycznego i magnetycznego są prostopadłe do kierunku rozchodzenia się fali.

Światło wysyłane przez większość źródeł jest skomplikowaną superpozycją fal harmonicznych o różnych częstotliwościach, wysyłanych przez różne atomy. Fale elektromagnetyczne spełniają zasadę superpozycji fal. Zasada ta głosi, że fale rozchodzą się w przestrzeni niezależnie od siebie. Zaburzenie w każdym punkcie przestrzeni, w której rozchodzi się kilka fal równocześnie, jest sumą zaburzeń pochodzących od poszczególnych fal. Superpozycja 2 lub więcej fal harmonicznych o tych samych częstotliwościach to interferencja.

• Fale świetlne podlegają również polaryzacji. Światło spolaryzowane - cechuje uporządkowanie drgań wektora świetlnego.

• Interferencja światła

• Inter światła nazywany nakładanie się (superpozycyjne) dwóch lub więcej fal o tych samych częstotliwościach powodujące odpowiednie wzmocnienie lub osłabienie natężenia powstającej fali wypadkowej.

• Dyfrakcja światła

• Dyfrakcja światła polega na tym, że podczas przechodzenia przez przeszkody (np. otwory, szczeliny) następuje wyraźne odchylenie od jego prostoliniowego rozchodzenia się. Zjawisko to daje się szczególnie obserwować w przypadku użycia wiązek laserowych. Zjawisko dyfrakcji tłumaczy się za pomocą tzw. zasady Huygensa mówiącej, że każdy punkt przesłony jest źródłem fali kulistej.

Efektem Comptona nazywamy zmianę długości fali elektromagnetycznej w wyniku rozpraszania jej na swobodnych elektronach. Zjawisko to można wyjaśnić przyjmując, że fala elektromagnetyczna o częstotliwości v i długości  jest strumieniem fotonów o energii E=hv(E= ) i wartości pędu p= .Wówczas rozpraszanie fali elektromagnetycznej rozpatrywać możemy jako proces zderzenia fotonów o pędzie p_of i energii E=hc/_o ze spoczywającymi elektronami. W wyniku tego zderzenia elektron uzyskuje pęd p_e ,a pęd fotonu maleje do wartości p_f. Tym samym długość rozpraszanej fali elektromagnetycznej zwiększa się do wartości =h/p_f. Równocześnie o kąt θ ulega zmianie kierunek propagacji fali. Zmianκ długości fali można wyznaczyć ze wzoru: ∆= (1 - cos θ), gdzie ∆=-_o, a θ - kΉt rozproszenia.

VI.

2*****

Oddziaływania międzycząsteczkowe - inne niż wiązania chemiczne siły wiążące atomy i cząsteczki.

Do oddziaływań tych zalicza się (w kolejności od najsilniejszych do najsłabszych):

• oddziaływania jon-jon nazywane też efektem jojo (kulombowskie lub elektrostatyczne) - zachodzą między dwiema różnoimiennie naładowanymi cząsteczkami; od wiązań jonowych różni je to, że ładunek w oddziałujących ze sobą cząsteczkach nie jest skoncentrowany na jednym atomie, lecz jest zdelokalizowany na kilku-kilkunastu atomach. Siła ich oddziaływania jest proporcjonalna do 1/r2 (gdzie r - odległość między cząsteczkami). W przypadku ośrodka zawierającego inne ładunki (np. roztworu elektrolitu) efekt oddziaływania jest mniejszy. (Zobacz też: para jonowa.)

• wiązanie wodorowe - tworzy się, gdy atom wodoru z cząstkowym ładunkiem dodatnim jest współdzielony przez dwie cząsteczki, które posiadają atomy z cząstkowym ładunkiem ujemnym. Wiązanie wodorowe, jeśli występuje w obrębie jednej cząsteczki, jest często traktowane jak słabe wiązanie chemiczne; jeśli jednak wiąże ono dwie lub więcej cząsteczek, można je traktować jako oddziaływanie międzycząsteczkowe

• oddziaływania trwały dipol - trwały dipol - tworzą się między cząsteczkami posiadającymi trwałe momenty dipolowe. Cząsteczki takie posiadają w jednych miejscach nadmiar ładunku ujemnego, a w innych jego niedomiar. Oddziałują one ze sobą tak jak jony - tyle, że oddziaływanie to jest słabsze, gdyż w grę wchodzą cząstkowe, a nie całkowite ładunki elektryczne, a także przyciąganiu pomiędzy ładunkami różnoimiennymi towarzyszy zawsze odpychanie pomiędzy ładunkami jednoimiennymi.

• oddziaływania van der Waalsa, zwane też oddziaływaniami Londona lub oddziaływaniami dyspersyjnymi - są to oddziaływania między trwałym dipolem i wzbudzonym dipolem lub między dwoma wzbudzonymi dipolami. W cząsteczkach, które nie posiadają trwałego momentu dipolowego, może on być wzbudzany przez cząsteczki z trwałym momentem; następnie taki wzbudzony dipol i trwały dipol oddziałują na siebie podobnie jak dwa trwałe dipole, tyle że znacznie słabiej. W cząsteczkach bez trwałego momentu dipolowego występują natomiast stochastyczne fluktuacje ich chmur elektronowych, powodujące powstawanie chwilowych momentów dipolowych. Cząsteczka posiadająca chwilowy moment dipolowy może go wzbudzić w cząsteczce sąsiadującej, wskutek czego obie cząsteczki mogą się nazwajem chwilowo przyciągać lub odpychać. Uśrednienie sił odpychających i przyciągających daje w wyniku oddziaływanie przyciągające proporcjonalne do 1/r6. Oddziaływania van der Waalsa wynikają m.in. z korelacji ruchów elektronów pomiędzy oddziałującymi atomami - dlatego w metodach obliczeniowych nieuwzględniających korelacji elektronowej sił tych praktycznie nie ma.

Należy również uwzględnić fakt, że dla małych odległości pomiędzy atomami czy cząsteczkami pojawia się oddziaływanie odpychające pomiędzy powłokami elektronowymi, wynikające z obowiązywania zakazu Pauliego.

3 Światłem potocznie nazywa się widzialną część promieniowania elektromagnetycznego, czyli promieniowanie widzialne odbierane przez siatkówkę oka ludzkiego np. światłocień. Precyzyjne ustalenie zakresu długości fal elektromagnetycznych nie jest tutaj możliwe, gdyż wzrok każdego człowieka charakteryzuje się nieco inną wrażliwością, stąd za wartości graniczne przyjmuje się maksymalnie 380-780 nm, choć często podaje się mniejsze zakresy (szczególnie od strony fal najdłuższych) aż do zakresu 400-700 nm.

Ale przykłady róznich zjawisk, no ja bym tutaj opisał zjawisko dyspersji, dyfrakcji itp. charakterystyczne dla fal elektro magnetycznych.

Dyfrakcja - ugięcie (zmiana kształtu czoła fali) na przeszkodzie, przy czym zjawisko to jest szczególnie wyraźne wtedy gdy rozmiary przeszkody są porównywalne z długością fali

Interferencja - nakładanie się fal, przy czym wychylenie fali wypadkowej jest algebraiczną sumą wychyleń fal składowych (superpozycja). W wyniku interferencji fale mogą się wzmacniać (fazy są zgodne), lub wygaszać (fazy przeciwne).

Polaryzacja - liniowa fali polega na uporządkowaniu drgań cząsteczek ośrodka do jednej płaszczyzny. Ulegają jej tylko fale poprzeczne

Odbicie - fala rozchodząca się w ośrodku sprężystym po dotarciu do jego granicy lub do jakiejś przeszkody może ulec odbiciu.

Prawo: Kąt padania alfa, jaki tworzy kier. Fali padającej z prostopadłą padania jest równy kątowi odbicia beta. Oba kąty leżą w tej samej płaszczyźnie.

Załamanie - jeżeli fala po dotarciu do granicy dwóch ośrodków wniknie do drugiego ośrodka i będzie się w nim rozchodzić to na tej granicy ulegnie załamaniu.

VII

2/3 Na przykładzie fal świetlnych wyjaśnij zjawiska interferencji, dyfrakcji i polaryzacji

Dyfrakcja światła (ugięcie) - zjawisko towarzyszące rozchodzeniu się światła, wykazujące odstępstwa od praw optyki geometrycznej. Jeżeli na drodze wiązki świetlnej znajduje się jakaś przeszkoda to dyfrakcja objawia się przenikaniem światła do wnętrza obszaru cienia albo inaczej ugięciem światła przy przechodzeniu obok krawędzi przeszkody. Dyfrakcja światła uwidacznia się przy przechodzeniu światła przez b. małe otwory (optymalnie gdy ich wielkość zbliżona jest do długości fali).

Interferencja światła - jest głównym świadectwem na falową strukturę światła. Interferencja jest szczególnym przypadkiem zjawiska superpozycji czyli nakładania się fal. Obserwować je można tylko przy spełnieniu następujących warunków:

Ciągi falowe muszą się przecinać,

Fale muszą być jednakowej długości i różnica faz z jaką się przecinają one w dowolnym punkcie w przestrzeni musi być stała w czasie (warunek koherencji).

Nakładanie się dwóch lub więcej wiązek, w wyniku czego wiązki lokalne wzmacniają się lub osłabiają. Natężenie wypadkowej fali świetlnej, powstałej w wyniku nałożenia się fal zależy od różnicy faz, typu fal. Jeżeli fazy są zgodne to następuje wzmocnienie, jeżeli przeciwne to osłabienie.

Charakterystyczną cechą fal poprzecznych jest zjawisko polaryzacji, czyli wyróżnione ustawienie wszystkich drgań fali w jednej, wspólnej płaszczyźnie.

***** oznacza, że wziąłem z wikipedii ;)

---