Patrycja Kuć
Roman Maciończyk
BADANIE UKŁADÓW DYSKRETNYCH
Układy dyskretne to takie gdzie przynajmniej jeden element układu działa w sposób dyskretny, tzn. jego sygnały mogą przyjmować tylko niektóre, wybrane wartości lub występują tylko w niektórych, wybranych chwilach czasu.
Przykład przebiegu sygnału na wyjściu elementów o działaniu:
ciągłym,
dyskretnym.
x(t) x(kTp)
t t
Tp
Tp- okres próbkowania
Urządzenie, które dokonuje próbkowania zapamiętuje okres próbkowania, dokonuje również ekstrapolacji(w tym przypadku rzędu 0).
Postać naszej transmitancji przedstawia się następująco:
![]()
Dokonujemy dyskretyzacji (Tp=1s, lc = 1, mc =[1 3 1];lc - licznik układu ciągłego, mc - mianownik układu ciągłego, Tp- okres próbkowania).
![]()
Przechodzimy teraz do opisu w postaci równania różnicowego :
x(k+1)≡Ax(k) + Bu(k)
y(k) =Cx(k)+Du(k)
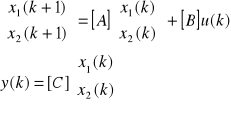
Dochodzimy do opisu macierzowego równania stanu oraz równania wyjścia:
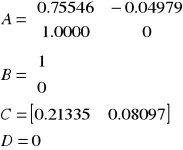
Zapis macierzowy :
Wartości własne macierzy A:
p1=0.6825
p2=0.0729
![]()
Obliczam zera i bieguny transmitancji (jak widać na wykresie):
zero: z= -0.3795
bieguny: p1=0.6825
p2=0.0729.
Jeśli p znajduje się w okręgu jednostkowym (okrąg o środku (0,0) i promieniu r=1) wówczas układ jest stabilny. Takie właśnie kryterium stabilności zostało przedstawione na wykresie) .Wystarczy, by jeden moduł z p był większy od jedności a wówczas układ staje się niestabilnym. O granicy stabilności mówimy wtedy, gdy moduł z p równe jest 1.
Układ jest aperiodyczny wtedy, gdy bieguny układu leżą na odcinku dodatniej osi rzeczywistej w przedziale (0,1).
Rozwiązując zJ-A =0 możemy sami wyznaczyć wartości własne układu.
Rozpatrując inny układ o następującej transmitancji (Tp=1) :
![]()
Przechodzimy do postaci dyskretnej naszej wyjściowej transmitancji, która będzie teraz wyglądać:
![]()
Opis macierzowy :
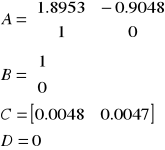
W tym przypadku zera i bieguny układu dyskretnego G(z) :
zero: z=-0.9672
bieguny: p1=0.9477+0.0823j
p2=0.9477-0.0823j
Dokonując analizy zauważamy, że układ jest stabilny (moduły są mniejsze od 1- wynoszą 0.9512), układ jest również aperiodyczny.
Chcąc rozpatrzyć przykład, gdy układ znajduje się na granicy stabilności przyjęliśmy następującą postać transmitancji ciągłej :
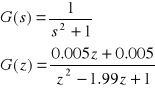
Na podstawie G(z) wyznaczamy zera i bieguny :
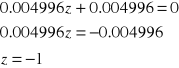
- zero
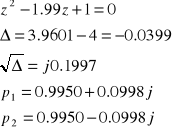
bieguny
![]()
Nasz układ jest periodyczny i znajduje się na granicy stabilności (wartość modułu=1).
![]()
![]()
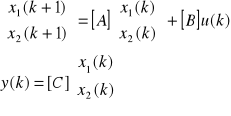
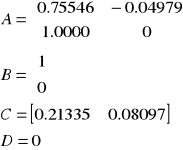
![]()
![]()
![]()
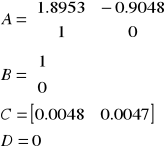
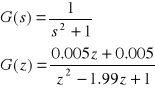
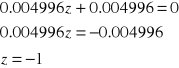
Wyszukiwarka
Podobne podstrony:
UKŁADY~1, ukŁady~1, Tabela
APD 5 układy bramkowe
Układy Napędowe oraz algorytmy sterowania w bioprotezach
Układy wodiociągowe ze zb przepł końcowym i hydroforem
uklady dyspersyjne
15 Uklady PLL i t s
W3B Układy fazowe
UKŁADY ENERGOELEKTRONICZNE W GRZEJNICTWIE 5F SZER
Uklady kombinacyjne
12 Podstawy automatyki Układy sterowania logicznego
Inf przestrz wekt uklady rown
5 Układy kogeneracyjne
F1 91 Układy arytmetyczne 6
więcej podobnych podstron