2

Blokowe kody liniowe

Historia liniowych kodów blokowych sięga roku 1950, kiedy to R. W. Hamming wprowadził klasę kodów korygujących pojedyncze błędy. Praktyczne znaczenie tych kodów było jednak ograniczone. Przełom w rozwoju teorii kodów blokowych wiąże się z opublikowaniem prac A. Hocquenghena (1959) oraz R. C. Bose'a i D. K. Ray-Chaudhuriego (1960). Wynaleźli oni dużą klasę kodów korygujących błędy wielokrotne, nazwanych na ich cześć kodami BCH. Kody BCH poznamy w następnym rozdziale.

2.1. Definicja blokowego kodu liniowego

Kodowanie blokowe polega na przekształcaniu k-pozycyjnych q-narnych ciągów informacyjnych

w n-pozycyjne q-narne ciągi kodowe

Nadmiar kodowy i sprawność kodu blokowego opisują zależności

(2.1)

(2.2)

Formalnie proces kodowania blokowego opisuje zależność

(2.3)

w której f jest funkcją określającą przyporządkowanie ciągów kodowych c ciągom informacyjnym h, czyli regułę kodowania. Oczywiście interesuje nas tylko przyporządkowanie wzajemnie jednoznaczne, to znaczy

(2.4)

Istotną cechą kodowania blokowego jest to, że proces kodowania w i-tym takcie nie zależy od przebiegu kodowania w poprzednich taktach, jak to pokazano symbolicznie na rysunku 2.1.

Blokowy kod nadmiarowy oznaczamy symbolem (n, k). Jednoznaczne określenie kodu (n, k) wymaga podania zbiorów {h} i {c} oraz funkcji f, najbardziej ogólna definicja blokowego kodu nadmiarowego ma więc postać

(2.5)

Rys. 2.1. Ilustracja procesu kodowania blokowego

Kod można przedstawić w postaci księgi kodowej, zawierającej wyszczególnienie wszystkich ciągów informacyjnych h oraz przyporządkowanych im ciągów kodowych c. Praktyczne znaczenie mają jednak niemal wyłącznie takie kody, dla których przyporządkowanie s = f(h) można przedstawić w postaci analitycznej. Posługiwanie się księgą kodową w procesie kodowania i dekodowania jest bowiem, nawet przy niezbyt dużych wartościach n i k, bardzo kłopotliwe.

Zbiór {h} k-pozycyjnych q-narnych ciągów informacyjnych i zbiór {z} wszystkich możliwych n-pozycyjnych ciągów q-narnych można traktować jako k-wymiarową i n-wymiarową przestrzeń liniową rozpiętą nad ciałem liczbowym CG(q). Zbiór {c} w ogólnym przypadku nie musi być przestrzenią, zależy to od właściwości funkcji f.

Najprostszym przekształceniem f odwzorowującym przestrzeń {h} w pewien podzbiór {c} przestrzeni {z} jest przekształcenie liniowe. Funkcja f jest przekształceniem liniowym, jeżeli dla dowolnych słuszna jest zależność

(2.6)

Jeśli przekształcenie f jest ponadto wzajemnie jednoznaczne, to nazywamy je izoformizmem. Zbiór {c} jest wówczas przestrzenią o wymiarze takim samym jak wymiar przestrzeni {h}:

(2.7)

Izomorfizm przekształca więc k-wymiarową przestrzeń {h} w k-wymiarową podprzestrzeń {c}, zanurzoną w n-wymiarowej przestrzeni {z}.

Najbardziej ogólna definicja blokowego kodu liniowego ma postać:

blokowy kod nadmiarowy jest kodem liniowym, jeśli przekształcenie f jest izomorfizmem.

Niech zbiór k liniowo niezależnych wektorów

stanowi bazę przestrzeni {h}, a zbiór n liniowo niezależnych wektorów

stanowi bazę przestrzeni {z}. Za pomocą funkcji f możemy odwzorować bazę na zbiór wektorów , należących do przestrzeni {z}, a więc stanowiących kombinacje liniowe wektorów bazy . Prowadzi t o do następującego układu równań:

(2.8)

Odwzorowanie bazy w przestrzeni {z} możemy przedstawić jako relację macierzową

(2.9)

w której:

stanowią macierze generujące przestrzenie {h} i {z}, a_li są natomiast elementami macierzy przekształcenia f w bazach A, B.

. (2.12)

Pokażemy teraz w jaki sposób ciąg informacyjny h odwzorowuje się za pośrednictwem przekształcenia liniowego f w odpowiadający mu ciąg kodowy c. Ciąg h przedstawiamy jako liniową kombinacją wektorów bazy

oraz korzystamy z liniowych właściwości funkcji f i zależności (2.8), otrzymujemy wówczas następujący ciąg przekształceń:

przy czym

stanowi i-ty współczynnik w kombinacji liniowej wektorów bazy odpowiadającej szukanemu ciągowi kodowemu c. Uzyskany wynik można przedstawić w postaci relacji macierzowej

(2.13)

w której k-pozycyjny wektor b określa liniową kombinację wektorów , a n-pozycyjny wektor - kombinację liniową wektorów odpowiadającą ciągowi kodowemu c. Przy zadanych bazach A i B oraz znanej funkcji f, ciąg kodowy c odpowiadający ciągowi informacyjnemu h wyznaczamy następująco:

- z równania określamy

- obliczamy ,

- wyznaczamy ciąg kodowy

Przykład 2.1

Znajdziemy zbiór ciągów kodowych binarnego kodu liniowego (5,3), traktowanego jako przekształcenie liniowe w bazach:

opisane przez macierz

Trójwymiarowe przestrzenie {h} i {c} oraz pięciowymiarowa przestrzeń {z} są rozpięte nad ciałem Galoisa CQ(2), którego elementami są: 0 - spełniające rolę elementu neutralnego względem operacji dodawania i 1 - spełniająca rolę elementu neutralnego względem operacji mnożenia (patrz Dodatek D-1.1).

Obliczamy macierz odwrotną względem macierzy A

Znajdziemy przykładowo ciąg kodowy s odpowiadający ciągowi informacyjnemu h = (011).

Iloczyn

Iloczyn

Ciąg kodowy

Przekształcenia wszystkich ośmiu ciągów informacyjnych na ciągi kodowe zestawiono w tabeli 2.1.

Tabela 2.1

Przekształcenie trzypozycyjnych ciągów informacyjnych
na pięciopozycyjne ciągi kodowe

h
0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1	0 0 0 1 1 1 1 0 1 0 1 0 1 0 0 0 1 1 0 0 1 1 1 0	0 0 0 0 0 0 0 1 0 0 1 1 0 1 1 1 1 1 1 1 1 0 1 0 0 1 0 0 0 0 0 1 1 1 1 0 1 0 1 1	0 0 0 0 0 0 0 1 1 1 0 1 1 0 1 0 1 0 1 0 1 1 1 1 1 1 1 0 0 0 1 0 0 1 0 1 0 1 0 1

Ten sam kod liniowy można przedstawić jako przekształcenie liniowe w różnych bazach. Ze względu na wygodę najczęściej stosuje się przekształcenie w bazach jednostkowych, dla którego relacja (2.13) przyjmuje postać

(2.14)

przy czym:

- macierze jednostkowe odpowiednich stopni,

- macierz przekształcenia liniowego w bazach jednostkowych.

Wprowadźmy oznaczenie

(2.15)

Relacja (2.14) przyjmie wówczas postać równania macierzowego

(2.16)

które nosi nazwę równania kodowania.

Macierz

(2.17)

nazywa się macierzą generującą blokowy kod liniowy (n, k).

Przykład 2.2

Zbadamy kod (5, 3) z przykładu 2.1, traktując go jako przekształcenie liniowe w bazach jednostkowych; mamy więc

oraz:

Macierz generująca kodu ma zatem postać

a równanie kodowania

Po wykonaniu mnożenia macierzowego dla wszystkich ciągów informacyjnych h otrzymujemy ciągi kodowe c zestawione w tabeli 1.

Oznaczmy przez

(2.19)

wektor odpowiadający i-temu wierszowi macierzy G. Wektory
są ciągami kodowymi, stanowiącymi układ k liniowo niezależnych wektorów. Inaczej mówiąc, zbiór
, i = 1, 2, ..., k, jest bazą przestrzeni kodowej. Zbiór wszystkich możliwych kombinacji liniowych wierszy macierzy G (przestrzeń wierszowa macierzy G) tworzy więc zbiór ciągów kodowych {c}. Fakt ten wyjaśnia nazwę macierzy G - macierz generująca kod.

Przykład 2.3

Pokażemy, że liniowe kombinacje wierszy macierzy G z przykładu 2.2 tworzą zbiór ciągów kodowych. W tym celu ponumerujemy wiersze macierzy

i wypiszemy wszystkie możliwe kombinacje liniowe:

Zbiór ten należy uzupełnić o ciąg złożony z samych zer.

W nietrywialnym przypadku w zbiorze {c} istnieje zwykle więcej niż jeden podzbiór k liniowo niezależnych ciągów kodowych, mogących pełnić rolę bazy przestrzeni kodowej. Stąd dla zadanego zbioru {c} istnieje nie jeden kod, lecz rodzina kodów liniowych (n,k), różniących się od siebie sposobem przyporządkowania {h}⇔{c}. Takie kody nazywamy ściśle równoważnymi kodami liniowymi. Otrzymuje się je wykonując na wierszach macierzy G operacje niezmiennicze (nie zmieniające przestrzeni {c}), którymi są:

• przestawienie wierszy miejscami,

• dodanie do wiersza dowolnej wielokrotności innego wiersza.

Przykład 2.4

Pokażemy dwa kody ściśle równoważne kodowi rozpatrywanemu w przykładzie 2.2. W tym celu utworzymy nowe macierze generujące: jedną (G') przez przestawienie wierszy, drugą (G'') przez umieszczenie w wierszu pierwszym sumy wiersza pierwszego i trzeciego, a w wierszu trzecim - sumy wiersza drugiego i trzeciego:

Uzyskane kody pokazano w tabeli 2.2.

Tabela 2.2

Kody ściśle równoważne

h	hG'	HG''
0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1	0 0 0 0 0 0 1 1 0 1 1 1 1 1 1 1 0 0 1 0 0 0 1 1 1 0 1 0 1 0 1 1 0 0 0 1 0 1 0 1	0 0 0 0 0 0 1 0 1 0 0 1 1 0 1 0 0 1 1 1 1 1 0 0 0 1 0 0 1 0 1 0 1 0 1 1 1 1 1 1

2.2 Kodowanie rozdzielne. Systematyczny blokowy kod liniowy

W zależności od sposobu wprowadzania nadmiaru informacyjnego kody blokowe dzielimy na kody rozdzielne i nierozdzielne. Kod blokowy (n, k) jest kodem rozdzielnym, jeśli zbiór n pozycji ciągu kodowego można rozdzielić na dwa rozłączne podzbiory: podzbiór pozycji informacyjnych
, dla których zachodzi równość

; (2.19)

oraz podzbiór n - k pozycji kontrolnych. W kodzie rozdzielnym na pozycjach informacyjnych ciągu kodowego c występuje jawnie ciąg informacyjny h. W ogólnym przypadku pozycje informacyjne i pozycje kontrolne mogą być przemieszane.

Zbadamy jakie warunki muszą być spełnione, aby blokowy kod liniowy był kodem rozdzielnym. Z zależności (2.16) i (2.17) wynika, że m-ta pozycja ciągu kodowego ma wartość

(2.20)

Po podstawieniu do wzoru (2.20) m = i_l oraz uwzględnieniu zależności (2.19), otrzymujemy

(2.21)

Oznacza to, że podmacierz

(2.22)

złożona z kolumn macierzy G o numerach
jest macierzą jednostkową.

Podmacierz złożoną z pozostałych kolumn macierzy G zapiszmy w postaci

(2.23)

Wartość j-tej pozycji kontrolnej opisuje zależność

j = 1,2,...,r. (2.24)

Rozdzielny kod liniowy (n, k) jest więc w pełni określony przez zbiór numerów pozycji informacyjnych oraz macierz P.

Szczególnym przypadkiem rozdzielnego kodu liniowego jest systematyczny kod liniowy. Jest to kod charakteryzujący się tym, że rolę pozycji informacyjnych pełni zbiór pierwszych k pozycji ciągu kodowego, to znaczy

Macierz generująca kodu systematycznego przybiera postać kanoniczną

(2.25)

przy czym
jest macierzą jednostkową stopnia k,
- macierzą zadającą kod, określoną wzorem (2.23). Kanoniczna postać macierzy G zapewnia przeniesienie ciągu informacyjnego h na k pierwszych pozycji ciągu kodowego, mamy bowiem

(2.26)

W pozostałych r pozycjach ciągu kodowego jest przesyłany ciąg kontrolny κ = określony wzorem

(2.27)

stanowiącym macierzowy zapis wzoru (2.24).

Nierozdzielny kod liniowy jest to taki kod (n, k), dla którego żaden podzbiór kolumn macierzy G nie stanowi macierzy jednostkowej. Dla dowolnego nierozdzielnego kodu liniowego istnieje co najmniej jeden ściśle równoważny kod rozdzielny. Warunkiem na to, by podzbiór pozycji
mógł pełnić rolę zbioru pozycji informacyjnych kodu ściśle równoważnego jest nieosobliwość macierzy
, opisanej wzorem (2.22).

Przykład 2.5

Dla kodu z przykładu 2.2 istnieje ściśle równoważny kod systematyczny, który otrzymujemy umieszczając w pierwszym wierszu macierzy generującej kod sumę pierwszego i drugiego wiersza macierzy G, w drugim wierszu - sumę drugiego i trzeciego wiersza macierzy G i pozostawiając trzeci wiersz bez zmiany

Macierz P ma więc postać : to znaczy, że pozycje kontrolne są opisane równaniami:

Ciągi kodowe mają postać:

0 0 0 0 0,

0 0 1 1 1,

0 1 0 1 0,

0 1 1 0 1,

1 0 0 1 0,

1 0 1 0 1,

1 1 0 0 0,

1 1 1 1 1.

2.3. Liniowe kody dualne. Macierz kontrolna kodu. Syndrom

W n-wymiarowej przestrzeni liniowej {z} złożonej z wszystkich możliwych q-narnych ciągów
n-pozycyjnych istnieje jedna i tylko jedna podprzestrzeń (n-k)-wymiarowa {v} związana z podprzestrzenią kodową {c}w ten sposób, że dla dowolnie wybranych znika iloczyn skalarny

(2.28)

Przestrzenie {c} i {v} nazywamy przestrzeniami ortogonalnymi, a odpowiadające im rodziny ściśle równoważnych kodów liniowych - kodami ortogonalnymi lub dualnymi. Kody dualne mają parametry (n, k) i (n, n-k), przy czym podzbiory pozycji informacyjnych i kontrolnych zamieniają się nawzajem miejscami. Ponieważ przestrzenie {c} i {v} określają się jednoznacznie, to kod liniowy (n, k) można określić - z dokładnością do kodu ściśle równoważnego - przez podanie macierzy H generującej kod dualny (n, n-k).

Ogólny dowód istnienia kodów dualnych pominiemy. Wykażemy natomiast, że dla systematycznego kodu liniowego generowanego przez macierz o postaci (2.25) istnieje kod dualny generowany przez macierz

, przy czym r = n - k. (2.29)

Oznaczmy wiersze macierzy G przez
a wiersze macierzy H przez Dowolne ciągi kodowe c i v możemy przedstawić jako liniowe kombinacje odpowiednio: wektorów

(2.30)

Po podstawieniu tych wyrażeń do zależności (2.28) i prostych przekształceniach otrzymujemy warunek zerowania się iloczynu skalarnego

(2.31)

który musi być spełniony dla dowolnych Musi zatem być: (2.32)

Układ równań (2.32) można przedstawić w zapisie macierzowym

(2.33)

przy czym jest k-wierszową i r-kolumnową macierzą złożoną z samych zer.

Wykażemy teraz, że macierz kontrolna H, opisana wzorem (2.29), spełnia równanie (2.33). Rzeczywiście

Macierz H nazywa się macierzą kontrolną kodu (n, k). Dla kodów binarnych (q = 2) wyrażenie (2.29), opisujące macierz kontrolną, przyjmuje postać

(2.34)

Przykład 2.6

Znajdziemy macierz kontrolną systematycznego binarnego kodu liniowego (7, 4), generowanego przez macierz

Macierz zadająca kod P (trzy ostatnie kolumny macierzy G) i macierz transponowana
mają postać:

Macierz kontrolną obliczamy z wzoru (2.34)

Macierz H generuje blokowy kod liniowy (7, 3), dualny względem rozpatrywanego kodu
(7, 4).

Z macierzą kontrolną kodu wiąże się pojęcie syndromu błędów, zwanego krótko syndromem. Syndrom n-pozycyjnego ciągu a definiujemy następująco

(2.35)

Syndrom jest r-pozycyjnym wektorem, którego j-tą pozycję opisuje zależność

(2.36)

przy czym
jest j-tym wierszem macierzy kontrolnej H.

Z zależności (2.32) wynika, że syndrom ciągu kodowego jest zerowy

(2.37)

Badanie wartości syndromu umożliwia więc stwierdzenie czy odebrany ciąg r jest ciągiem kodowym. Macierzowemu równaniu (2.37) odpowiada układ r równań liniowych o postaci

(2.38)

przy czym sumowanie jest sumowaniem modulo q.

Równania (2.38) nazywamy testami kontrolnymi kodu liniowego. Określają one charakterystyczne dla danego kodu liniowe zależności pomiędzy pozycjami ciągu kodowego. Testy kontrolne stanowią wiersze macierzy H, przy czym pozycjom wchodzącym do j-tego testu odpowiadają niezerowe wyrazy j-wiersza. W przypadku kodu binarnego (q = 2) równania (2.38) nazywamy testami parzystości.

Przykład 2.7

Testy parzystości dla macierzy H z przykładu 2.6 mają postać:

2.4. Metryka przestrzeni kodowej. Odległość minimalna kodu

Dowolny q-narny kod nadmiarowy (n, k) możemy traktować jako pewien podzbiór {c} elementów n-wymiarowej przestrzeni {z} rozpiętej nad ciałem CG(q), przy czym w przypadku kodu liniowego zbiór {c} jest k-wymiarową podprzestrzenią przestrzeni {z}. Na jeden ciąg kodowy c w przestrzeni {z} przypada średnio
ciągów niekodowych. Z tego faktu wynika możliwość wykrywania i korygowania niektórych błędów, powstałych podczas transmisji sygnału. O tym, które ciągi błędów będą wykrywane (korygowane) decyduje rozmieszczenie ciągów kodowych w przestrzeni {z}, to znaczy geometria kodu. Mogą zatem istnieć kody o identycznych parametrach n,k, ale różnych właściwościach detekcyjno-korekcyjnych. Z tego względu często uzupełnienia się symbol kodu dodatkowym parametrem t określającym liczbę błędów, które kod może skorygować, tak więc pełne oznaczenie liniowego kodu blokowego ma postać (n, k, t). Na przykład symbol (15, 5, 3) oznacza kod, którego ciągi mają 15 elementów, w tym 5 elementów informacyjnych, i który może skorygować trzy błędy.

Analizę właściwości kodów nadmiarowych ułatwia zdefiniowanie metryki przestrzeni {z}, to jest miary odległości pomiędzy dowolnymi "punktami" (elementami) tej przestrzeni. Jeżeli a,b,c {z}, to miara odległości d(a,b) musi spełniać następujące aksjomaty:

(1) d(a,b) 0; d(a,b) = 0 tylko dla a = b;

(2) d(a,b) d(a,c) + d(c,b);

(3) d(a,b) = d(b,a).

Można znaleźć więcej niż jedną funkcję d(a,b) spełniającą podane aksjomaty. Ograniczymy się do omówienia metryki Hamminga i metryki Lee.

2.4.1. Metryka Hamminga

Wagą Hamminga pozycji
ciągu a nazywamy liczbę

(2.39)

Wagą Hamminga ciągu a nazywamy sumę wag jego pozycji

(2.40)

Odległością Hamminga między ciągami a, b nazywamy liczbę

(2.41)

Łatwo zauważyć, że d(a,b) jest liczbą pozycji, w których ciągi a, b różnią się. Podkreślmy jeszcze, że metryka Hamminga nie uwzględnia wartości liczbowych niezerowych pozycji ciągów.

Przykład 2.8

Obliczymy odległość Hamminga między ciągami a = (0 4 1 2 0 3) i b = (3 0 1 4 1 2), których elementy należą do ciała CG(5) = {0, 1, 2, 3, 4}. Wagi poszczególnych pozycji ciągów są następujące:

i	1	2	3	4	5	6
ai	0	4	1	2	0	3
	0	1	1	1	0	1
bi	3	0	1	4	1	2
	1	0	1	1	1	1
ai - bi	-3	4	0	-2	-1	1

Wagi ciągów:

Odległość między ciągami

W przypadku ciągów binarnych (q = 2) liczbową wartość wagi Hamminga ciągu a możemy obliczyć ze wzoru

(2.42)

traktując formalnie elementy 0 i 1 ciała CG(2) jako liczby rzeczywiste, innymi słowy waga Hamminga ciągu jest równa liczbie zawartych w nim jedynek. Odległość pomiędzy ciągami binarnymi obliczamy z zależności

(2.43)

Przykład 2.9

Rozpatrzmy dwa pięciopozycyjne ciągi binarne: a = (1 0 0 0 1) i b = (1 1 1 1 1). Waga ciągu a wynosi 2, ciągu b - 5. Odległość pomiędzy ciągami wynosi 3, bowiem a + b = (0 1 1 1 0).

Dla q = 2 przestrzeń {z} możemy interpretować jako zbiór wierzchołków pewnego
n-wymiarowego "wielościanu foremnego". Odległość Hamminga pomiędzy binarnymi
n-pozycyjnymi ciągami a i b stanowi wówczas liczba krawędzi jaką należy przebyć, aby startując od ciągu a i poruszając się po krawędziach najkrótszą drogą osiągnąć ciąg b. Na rysunku 2.1 pokazano przestrzeń dla q = 2 i n = 3. Zauważmy, że w odległości d = 2 od dowolnie wybranego punktu (000) leżą trzy punkty: (011), (101) i (110); w odległości d = 3 leży tylko jeden punkt (111).

Rys. 2.1. Binarna przestrzeń trójwymiarowa; w odległości d = 2 od wybranego punktu (000) leżą

trzy punkty: (011), (101) i (110); w odległości d = 3 leży tylko jeden punkt (111)

2.4.2. Metryka Lee

W wielu przypadkach prawdopodobieństwo wystąpienia błędów elementarnych różnego rodzaju nie jest jednakowe. Na przykład przy stosowaniu modulacji fazy prawdopodobieństwo przekłamania sygnału jest malejącą funkcją wartości zmiany fazy odpowiadającej dwóm sąsiednim sygnałom. W takich przypadkach korzystniejszą jest metryka Lee, oparta na pojęciach wagi Lee pozycji a_i ciągu a oraz wagi Lee ciągu a, zdefiniowanych następująco.

Waga Lee pozycji a_i q-narnego ciągu a

(2.44)

Wagą Lee n-pozycyjnego q-narnego ciągu a nazywa się sumę wag jego pozycji

(2.45)

Odległość Lee dwóch n-pozycyjnych q-narnych ciągów a i b definiuje się jako

(2.46)

Mimo podobieństwa wzorów (2.43) i (2.46) odległość Hamminga i odległość Lee są różnymi wielkościami. Metryki te utożsamiają się liczbowo tylko dla q = 2 i q = 3.

Przykład 2.10

Obliczymy odległość Lee między ciągami rozpatrywanymi w przykładzie 2.8.

Ponieważ q = 5, więc wagi poszczególnych pozycji, zgodnie ze wzorem(2.44), wynoszą:

i	1	2	3	4	5	6
ai	0	4	1	2	0	3
bi	3	0	1	4	1	2
ai - bi	-3	4	0	-2	-1	1
	2	1	0	2	1	1

Odległość Lee

2.5. Odległość minimalna. Zdolność detekcyjna i korekcyjna kodu nadmiarowego

Intuicyjnie wyczuwamy, że im większe są odległości między poszczególnymi ciągami kodowymi, tym mniej prawdopodobne jest przekłamanie przesyłanego ciągu kodowego na jakiś inny ciąg kodowy. Jakość kodu nadmiarowego można więc oszacować na podstawie minimalnej odległości między ciągami kodowymi. Odległość tę, nazywaną odległością minimalną kodu nadmiarowego, definiujemy następująco:

(2.47)

Wprowadzenie pojęcia odległości minimalnej umożliwia w prosty sposób określenie zdolności detekcyjnych i korekcyjnych kodu liniowego.

Dekodowanie detekcyjne. Dekoder nie wykrywa tylko takich ciągów błędów, które zamieniają ciąg nadany na jakiś inny ciąg kodowy. Tego typu przekłamanie wymaga wystąpienia błędów w liczbie nie mniejszej niż odległość minimalna kodu. Największa krotność błędów wykrywanych przez blokowy kod nadmiarowy (n, k) o odległości minimalnej wynosi więc

(2.48)

Dekodowanie korekcyjne. Optymalną regułą decyzyjną w przypadku dekodowania korekcyjnego jest reguła maksymalizująca prawdopodobieństwo a posteriori P(cy) nadania ciągu c = c^*, przy warunku że został odebrany ciąg y. Reguła ta, nazywana regułą największego prawdopodobieństwa, minimalizuje prawdopodobieństwo błędnej decyzji dekodera.

Formalnie optymalną regułę dekodowania korekcyjnego zapisujemy w postaci:

(2.49)
i = 1,2,...,q^k; i ≠ l.

Dekoder działający według reguły (2.49) przeszukuje w przestrzeni {z} najbliższe otoczenie odebranego ciągu y i podejmuje decyzję, że został nadany taki ciąg c_l, który leży w najmniejszej odległości od ciągu y. Biorąc pod uwagę, że w zbiorze {c} istnieje co najmniej jedna para ciągów odległych od siebie o d_min oraz że decyzje dekodera muszą być jednoznaczne, dochodzimy do wniosku, że największa krotność błędów korygowanych przez liniowy kod blokowy o odległości minimalnej d_min wynosi

(2.50)

przy czym oznacza część całkowitą liczby x.

2.6. Graniczne właściwości blokowych kodów liniowych

Zależności (2.48) i (2.50) umożliwiają określenie największej krotności błędów wykrywanych i korygowanych przez kod (n, k) o znanej odległości minimalnej d_min. Odrębne zagadnienie polega na znalezieniu wartości t, którą można osiągnąć przy ustalonych wartościach n i k. Oznaczmy przez A_l podzbiór zbioru {z}, złożony z n-pozycyjnych q-narnych ciągów leżących w odległości nie większej niż t od ustalonego ciągu kodowego c_l

(2.51)

Moc zbioru A_l nie zależy od wyboru c_l i wynosi

(2.52)

Jeżeli kod koryguje błędy o krotności t, to podzbiory A_l muszą być rozłączne. Biorąc pod uwagę, że moc zbioru {c} wynosi q^k, a moc zbioru {z} wynosi qⁿ, otrzymujemy oczywistą nierówność
którą możemy sprowadzić do postaci

(2.53)

pamiętając, że n - k = r. Nierówność (2.53) nazywamy nierównością Hamminga. Graniczny przypadek tej nierówności

(2.54)

nazywamy kresem górnym Hamminga, a kod osiągający ten kres - kodem idealnym lub kodem gęsto upakowanym. Charakterystyczną cechą kodu idealnego jest to, że jego nadmiar kodowy jest w pełni wykorzystany. Rzeczywiście, wartość liczbowa prawej strony równania (2.54) odpowiada liczbie różnych ciągów błędów, jakie poprawnie koryguje kod z parametrem t, lewa strona równania wyznacza natomiast liczbę różnych postaci syndromu. Syndromów jest więc dokładnie tyle, ile wynosi liczba sytuacji, jakie musi rozróżniać dekoder. Kodami idealnymi są kody Hamminga o parametrach oraz kod Golaya o parametrach (23,12) i d_min = 7. Jeśli dla zadanych wartości n i k nie istnieje kod idealny, to kod (n, k) o największej wartości d_min nazywamy kodem optymalnym.

2.7. Dekodowanie korekcyjne blokowego kodu liniowego

Dekodowanie korekcyjne blokowego kodu liniowego opiera się na tak zwanej tablicy dekodowania. Tablicę tę tworzy się poprzez rozłożenie grupy {z} na warstwy względem podgrupy, jaką jest zbiór ciągów kodowych {c}. Konstrukcja tabeli przebiega następująco (tab. 2.3). Pierwszą warstwę stanowią elementy będące ciągami kodowymi , przy czym jako pierwszy element (z lewej) umieszcza się ciąg ζ₁ złożony z samych zer i pełniący rolę elementu neutralnego w grupie. Następnie ze zbioru {z} wybiera się niekodowe ciągi o wadze 1 i umieszcza kolejno pod ciągiem ζ₁ jako elementy tworzące warstwy. Pozostałe elementy każdej warstwy powstają w wyniku sumowania elementu tworzącego warstwę z elementami pierwszej warstwy (ciągami kodowymi). W dalszej kolejności wybiera się ciągi o wadze 2 i większej i postępuje podobnie jak z ciągami o wadze 1. W wyniku takiego postępowania powstaje tablica złożona z q^r warstw po p elementów, łącznie elementów, co stanowi całą przestrzeń {z}.

Tabela 2.3

Tablica dekodowania q-narnego blokowego kodu liniowego (n, k)

		…		…
		…		…
…	…	…	…	…	…
		…		…
…	…	…	…	…	…
		…		…

Tablica dekodowania charakteryzuje się kilkoma właściwościami, które podamy bez dowodu:
• w tablicy nie występują powtarzające się elementy,

• elementy tej samej warstwy mają ten sam syndrom,

• różnica dwóch ciągów należących do tej samej warstwy jest ciągiem kodowym,

• różnica dwóch ciągów należących do różnych warstw nie jest ciągiem kodowym,

• elementy należące do różnych warstw mają różne syndromy,

• w tej samej warstwie nie może wystąpić więcej niż jeden ciąg o wadze większej niż zdolność korekcyjna kodu t,

• oznaczmy kolumnę tablicy dekodowania zawierającą ciąg kodowy c_l przez Γ_l; dla i ≠ l nie istnieje żaden taki ciąg kodowy c_i, który leżałby bliżej ciągów z należących do kolumny Γ_l niż ciąg kodowy c_l.

Korygowanie błędów opiera się na następującej regule:

jeżeli (2.55)

Reguła ta zapewnia poprawne korygowanie takich i tylko takich błędów, które należą do zbioru elementów tworzących warstwy {ζ}. Jest to reguła optymalna.

Dekodowanie korekcyjne przebiega w trzech etapach:

• obliczenie syndromu S(y) odebranego ciągu y,

• odszukanie, na podstawie S(y), elementu ζ tworzącego warstwę, w której leży ciąg y,

• skorygowanie błędów według zależności

Przykład 2.11

Skonstruujemy tablicę dekodowania dla blokowego kodu liniowego (7, 4), którego macierze: generująca i kontrolna mają postacie:

Zbiór ciągów kodowych ma postać:

0000000	0001011	0111010	1111111
1011000	1110100	0100111	1000101
0101100	1001110	0011101	0110001
0010110	1010011	1100010	1101001

Postępując zgodnie z procedurą opisaną w p. 2.7 otrzymujemy następującą tablicę dekodowania (tab. 2.4).

W ostatniej kolumnie tablicy dekodowania wpisano syndromy elementów tworzących warstwy. Odległość minimalna kodu jest równa 3, kod zapewnia więc poprawne korygowanie błędów pojedynczych.

Załóżmy, że nadany został ciąg 1100010 oraz że podczas transmisji wystąpiło przekłamanie na trzeciej pozycji, to znaczy że ciąg odebrany ma postać 1110010. Syndrom tego ciągu jest równy 111, odpowiada mu element tworzący 0010000. Skorygowany ciąg ma więc postać

c^* = 1110010 + 0010000 = 1100010.

Korekcja została zatem przeprowadzona poprawnie.

2.8. Przegląd wybranych kodów liniowych

Kod z kontrolą parzystości jest najprostszym binarnym blokowym kodem liniowym. Ciąg kodowy tego kodu powstaje w wyniku dołączenia do ciągu informacyjnego jednej pozycji kontrolnej, sprawdzającej parzystość jedynek w ciągu informacyjnym. Kod ma więc parametry
(n, n-1), a równanie kodowania ma postać

,

w której symbol oznacza wieloargumentową sumę modulo dwa.

Macierz generująca kodu

,

przy czym jest kolumną lub wierszem złożonym z m jedynek.

Macierz kontrolna

.

Kod z kontrolą parzystości ma odległość minimalną równą 2 oraz sprawność . Kod wykrywa pojedyncze błędy.

Kod z m-krotnym powtarzaniem powstaje w wyniku m-krotnego powtórzenia ciągu informacyjnego

.

Kod ma oznaczenie (mk, k), a macierze: generująca i kontrolna przybierają postacie:

, .

Odległość minimalna i sprawność kodu określają zależności:

, .

Kodem iterowanym m-krotnie nazywamy kod, którego ciągi powstają w wyniku m-krotnego kodowania informacji m kodami (niekoniecznie jednakowymi) według następujących reguł:

1. Ciąg informacyjny h o długości przedstawia się w postaci m-wymiarowego "prostopadłościanu" o wymiarach w układzie współrzędnych

2. Podciągi informacyjne o długości , umieszczone równolegle do osi , koduje się kodem . W wyniku tej operacji powstaje prostopadłościan o wymiarach .

3. Podobnie, podciągi informacyjne o długości ,umieszczone równolegle do osi , koduje się kodem otrzymując prostopadłościan o wymiarach .

4. Postępując w ten sposób ze wszystkimi podciągami informacyjnymi, tzn. kodując je kodami otrzymujemy ciąg kodowy w postaci m-wymiarowego prostopadłościanu o wymiarach

Uzyskany w ten sposób ciąg kodowy jest wprowadzany do kanału szeregowo, pozycja po pozycji, przy czym kolejność wysyłania pozycji jest obojętna (ale ustalona). Po stronie odbiorczej odebrany ciąg jest przedstawiany w postaci m-wymiarowego prostopadłościanu, z uwzględnieniem przyjętej zasady tworzenia ciągu kodowego przed wysłaniem go w kanał, a następnie dekodowny kolejno kodami (n_m, k_m), (n_m-1, k_m-1), ..., (n₁, k₁).

Oznaczenie kodu iterowanego ma postać , a jego parametry są następujące:

- odległość minimalna: - sprawność:

Jeżeli iterowanie odbywa się na podstawie jednego kodu o parametrach: to parametry kodu iterowanego są następujące: ; .

Na przykład kod dwukrotnie iterowany (40, 16) można uzyskać stosując następujące dwa kody:
kod z powtarzaniem (8, 4) o sprawności i odległości minimalnej oraz kod z kontrolą parzystości (5, 4) o sprawności i odległości minimalnej

Elementy ciągu informacyjnego dzielimy na cztery grupy po cztery elementy w grupie, które ustawiamy jedna pod drugą. Kodowanie kodem z powtarzaniem (8, 4) polega na powtórzeniu zapisu każdej grupy. Kodowanie kodem z kontrolą parzystości polega na sprawdzeniu liczby jedynek w kolumnach i dodaniu zera lub jedynki, tak aby liczba jedynek w kolumnie była parzysta.

Ilustrację kodowania kodem dwukrotnie iterowanym (40, 16) ciągu informacyjnego

h = 100111000011100

pokazano w tabeli 2.5.

Tabela 2.5.

Konstrukcja ciągu kodowego kodu dwukrotnie iterowanego
na bazie kodu z powtarzaniem (8, 4) i kodu z kontrolą parzystości (5, 4)

1	0	0	1	1	0	0	1
1	1	0	0	1	1	0	0
0	0	1	1	0	0	1	1
1	0	0	0	1	0	0	0
1	1	1	0	1	1	1	0

Ciąg kodowy uzyskuje się sczytując kolejno wiersze tabeli, mamy więc

c = 1001100111001100001100111000100011101110.

Odległość minimalna kodu wynosi sprawność -

Kodem Hamminga nazywa się obecnie każdy blokowy kod liniowy (n, k), spełniający kres górny Hamminga dla t = 1. Kody Hamminga mają parametry: przy czym - m jest liczbą naturalną. Przykładem kody Hamminga może być kod (7, 4) generowany przez macierz

.

Macierz kontrolna tego kodu ma postać

.

Wydłużony kod liniowy powstaje z kodu liniowego o nieparzystej odległości minimalnej Procedura wydłużania polega na wprowadzeniu do wyjściowego ciągu kodowego dodatkowej pozycji kontrolnej, sprawdzającej parzystość jedynek według reguły

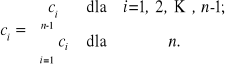
Wydłużony kod liniowy ma parzystą odległość minimalna

Procedurę wydłużania można stosować do dowolnego kodu liniowego o nieparzystej odległości minimalnej. Na przykład wydłużony kod Hamminga (8, 4), powstały z kodu (7, 4), jest generowany przez macierz

,

a macierz kontrolna ma postać

.

Kodem równoodległym nazywamy taki kod liniowy, którego ciąg kodowy ma jako pozycje wszystkie możliwe niezerowe kombinacje liniowe pozycji ciąg informacyjnego. Ciąg kodowy binarnego kodu równoodległego zawiera:

pozycji informacyjnych:

pozycji kontrolnych typu

pozycji kontrolnych typu

pozycję kontrolną typu

Długość ciągu więc oznaczenie kodu

Odległość minimalna

Na przykład dla k = 4 otrzymuje się kod równoodległy (15, 4), którego ciągi opisuje zależność

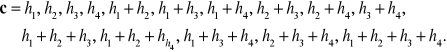
Macierze generująca i kontrolna rozpatrywanego kodu mają postaci:

,

.

Zbiór ciągów kodowych:

0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
0	0	0	1	0	0	1	0	1	1	0	1	1	1	1
0	0	1	0	0	1	0	1	0	1	1	0	1	1	1
0	0	1	1	0	1	1	1	1	0	1	1	0	0	0
0	0	1	0	0	1	0	1	0	1	1	0	1	1	1
0	1	0	1	1	0	1	1	0	1	1	0	1	0	0
0	1	1	0	1	1	0	0	1	1	0	1	1	0	0
0	1	1	1	1	1	1	0	0	0	0	0	0	1	1
1	0	0	0	1	1	1	0	0	0	1	1	1	0	1
1	0	0	1	1	1	0	0	1	1	1	0	0	1	0
1	0	1	0	1	0	1	1	0	1	0	1	0	1	0
1	0	1	1	1	0	0	1	1	0	0	0	1	0	1
1	1	0	0	0	1	1	1	1	0	0	0	1	1	0
1	1	0	1	0	1	0	1	0	1	0	1	0	0	1
1	1	1	0	0	0	1	0	1	1	1	0	0	0	1
1	1	1	1	0	0	0	0	0	0	1	1	1	1	0

Odległość minimalna

Kodem Mac Donalda nazywa się kod liniowy, którego ciąg kodowy zawiera:

- pozycje informacyjne w liczbie k, dla których zachodzi

- pozycje kontrolne w postaci niezerowych, co najmniej dwuargumentowych kombinacji liniowych pozycji ciągu informacyjnego.

W ogólnym przypadku pozycjami kontrolnymi ciągu kodowego kodu Mac Donalda mogą być nie wszystkie kombinacje liniowe pozycji ciągu informacyjnego, jak to ma miejsce w przypadku kodu równoodległego, który jest szczególnym przypadkiem kodu Mac Donalda.

Jeśli na przykład z omawianego wcześniej kodu równoodległego (15, 4) usuniemy formy , to otrzymamy kod Mac Donalda (7, 4), którego ciągi kodowe opisuje zależność

Macierze generująca i kontrolna mają postaci:

G = ,

Zbiór ciągów kodowych:

0	0	0	0	0	0	0	0	0
0	0	0	1	0	1	1	1	1
0	0	1	0	1	0	1	1	1
0	0	1	1	1	1	0	0	0
0	0	1	0	1	0	1	1	1
0	1	0	1	1	0	1	0	0
0	1	1	0	0	1	1	0	0
0	1	1	1	0	0	0	1	1
1	0	0	0	1	1	1	0	1
1	0	0	1	1	0	0	1	0
1	0	1	0	0	1	0	1	0
1	0	1	1	0	0	1	0	1
1	1	0	0	0	0	1	1	0
1	1	0	1	0	1	0	0	1
1	1	1	0	1	0	0	0	1
1	1	1	1	1	1	1	1	0

Odległość minimalna d_min = 4.

Kody Reeda-Mullera (kody RM) stanowią interesującą grupę kodów liniowych. Parametry binarnych kodów RM są następujące:

przy czym m, - liczby naturalne ; - rząd kodu.

Konstrukcja kodów RM opiera się na n-wymiarowej przemiennej i łącznej algebrze, jaka powstaje w wyniku wprowadzenia w n-wymiarowej przestrzeni liniowej operacji mnożenia wektorowego ciągów, zdefiniowanej następująco:

Dla zadanej wartości m konstruuje się algebrę, której bazę stanowią następujące n-pozycyjne ciągi binarne:

ciąg
złożony z samych jedynek;

m ciągów
które wypisane pod sobą tworzą macierz o kolumnach będących m-pozycyjnymi ciągami binarnymi;

ciągów typu

ciągów typu

aż do ciągu typu

Baza składa się z
ciągów. Na przykład baza ma postać:

u0	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
u1	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
u2	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
u3	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
u4	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
u12	0	0	0	0	0	0	0	0	0	0	0	0	1	1	1	1
u13	0	0	0	0	0	0	0	0	0	0	1	1	0	0	1	1
u14	0	0	0	0	0	0	0	0	0	1	0	1	0	1	0	1
u23	0	0	0	0	0	0	1	1	0	0	0	0	0	0	1	1
u24	0	0	0	0	0	1	0	1	0	0	0	0	0	1	0	1
u34	0	0	0	1	0	0	0	1	0	0	0	1	0	0	0	1
u123	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	1
u124	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	1
u134	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	1
u234	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	1
u1234	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1

Kod RM rzędu jest kod liniowy generowany przez macierz G, której wierszami są następujące elementy (ciągi) bazy oraz wszystkie ciągi
.

Kod RM ma odległość minimalną

Kodem dualnym do kodu RM rzędu jest kod RM rzędu

Rozpatrzymy kod RM z
Macierz generująca ma postać

Macierz kontrolna

Parametry kodu:

Kod RM z jest równoważny kodowi z kontrolą parzystości.

Kod RM z jest równoważny wydłużonemu kodowi Hamminga.

Daniel Józef Bem, Blokowe kody liniowe Strona 20

---