LABOLATORIUM ELEKTROTECHNIKI TEORETYCZNEJ

Temat ćwiczenia numer 4.:Linia długa

Ćwiczenie wykonał: rok IImgr

Ćwiczenie wykonane dnia:6.11.95

1.Schemat pomiarowy oraz używane wzory.

Wzory i oznaczenia używane w rozważaniach.

U, I -wartości w dowolnym miejscu linii,

U_p, I_p -wartości fali początkowej w dowolnym miejscu linii,

U_o, I_o -wartości fali odbitej w dowolnym miejscu linii,

U₂, I₂ -wartości na obciążeniu linii,

Z_f -impedancja falowa linii,

Z₂ -impedancja obciążenia linii,

n -współczynnik odbicia.

U=U_p+U_o I=I_p+I_o

Z_f=U_p/I_p=U_o/I_o=U/I Z₂=U₂/I₂

n=(Z₂-Z_f)/(Z₂+Z_f)=U_o(l)/U_p(l)=I_o(l)/I_p(l)2. Linia długa bez strat w stanie jałowym.

	l-x	α	wskaźnik
Lp.			napięcia	prądu
	[cm]	[dz]	--	--
1.	0	40	X
2.	10	40	X
3.	20	32
4.	30	18		X
5.	40	2		X
6.	50	22	X	X
7.	60	38	X	X
8.	70	48	X
9.	80	50	X
10.	90	46	X
11.	100	36
12.	110	20
13.	120	2		X
14.	130	18		X
15.	140	32	X	X

Obliczenia i wnioski.

- obliczamy U₂, I₂

Z₂=∞ czyli I₂=0

n=1

U_o(l)=U_p(l) I_o(l)=I_p(l)

U₂=U_p(l)+U_o(l)=2U_p(l) I₂=I_p(l)-I_o(l)=0

Porównując obliczenia i pomiary dane się potwierdzają.

-wyznaczamy węzły fali napięciowej

u(t), i(t) wartości chwilowe na linii

u(t)=U₂ √2 cos(2π(l-x)/λ) cos ωt

i(t)=U₂√2/Z_f sin(2π(l-x)/λ) cos ωt

λ=c/f=3*108 m/s / 181*106 Hz= 165 cm

dla l-x=(2k+1)λ/4 k=0, 1, 2, 3...

występują węzły fali napięciowej ( l-x=41 i 123 cm )

Punkty węzłów z obliczeń i pomiarów pokrywają się.

3. Linia długa bez strat w stanie zwarcia.

	l-x	α	wskaźnik
Lp.			napięcia	prądu
	[cm]	[dz]	--	--
1.	0	22		X
2.	10	60	X	X
3.	20	114		X
4.	30	132	X	X
5.	40	110	X
6.	50	94
7.	60	90	X
8.	70	60	X	X
9.	80	14		X
10.	90	38	X	X
11.	100	90	X	X
12.	110	128		X
13.	120	110	X
14.	130	94	X
15.	140	68

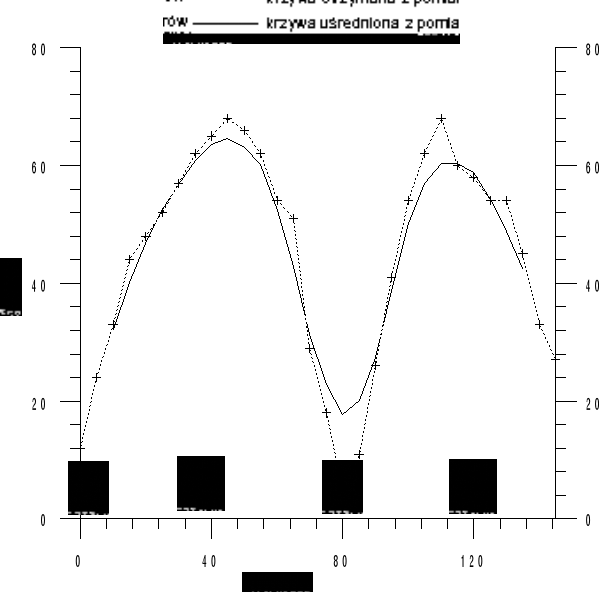
Obliczenia i wnioski.

- obliczamy U₂, I₂

Z₂=0 czyli U₂=0

n=-1

U_o(l)=-U_p(l) I_o(l)=-I_p(l)

U₂=U_p(l)+U_o(l)=0 I₂=I_p(l)-I_o(l)= 2I_p(l)

Porównując obliczenia i pomiary dane się potwierdzają.

-wyznaczamy węzły fali napięciowej

u(t), i(t) wartości chwilowe na linii

u(t)=I₂ Z_f √2 sin(2π(l-x)/λ) cos ωt

i(t)=I₂√2 cos(2π(l-x)/λ) sin ωt

dla l-x=2kλ/4 k=0, 1, 2, 3...

występują węzły fali napięciowej ( l-x=82 i 164 cm )

Punkty węzłów z obliczeń i pomiarów pokrywają się.

4. Linia długa bez strat pod obciążeniem falowym Z_f=R=243 Ω.

	l-x	α
Lp.
	[cm]	[dz]
1.	0	18
2.	10	18
3.	20	18
4.	30	18
5.	40	18
6.	50	16
7.	60	16
8.	70	18
9.	80	18
10.	90	18
11.	100	20
12.	110	20
13.	120	18
14.	130	18
15.	140	18

Obliczenia i wnioski.

Z₂=Z_f n=0

występuje całkowite pochłanianie fali odbitej, czyli U₂=Z_f*I₂,

wartości U, I są stałe na całej linii, co obserwujemy na wykresie5. Linia długa bez strat obciążona rezystancją 2Z_f=R=486Ω

	l-x	α
Lp.
	[cm]	[dz]
1.	0	26
2.	10	26
3.	20	20
4.	30	16
5.	40	14
6.	50	18
7.	60	22
8.	70	28
9.	80	28
10.	90	28
11.	100	26
12.	110	18
13.	120	16
14.	130	18
15.	140	20

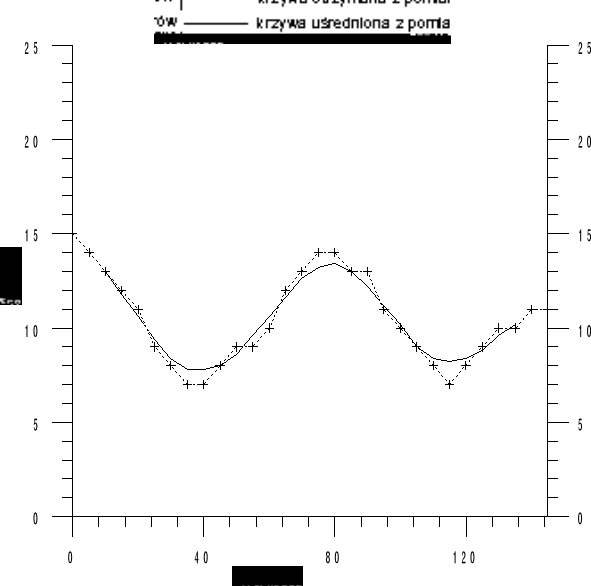
Obliczenia i wnioski.

- obliczamy U₂, I₂

Z₂=486Ω

n=U_o(l)/U_p(l)=1/3

U_o(l)=1/3*U_p(l) I_o(l)=1/3*I_p(l)

U₂=U_p(l)+U_o(l)=4/3*U_p(l) I₂=I_p(l)-I_o(l)=2/3*I_p(l)

Fala odbita jest częściowo pochłaniana.

Porównując obliczenia i pomiary dane się potwierdzają.

Węzły fali napięciowej występują w tym samym miejscu, co w przypadku linii w stanie jałowym.6. Linia długa bez strat obciążona reaktencją C=3pF.

	l-x	α	wskaźnik
Lp.			napięcia	prądu
	[cm]	[dz]	--	--
1.	0	30	X
2.	10	30
3.	20	10		X
4.	30	18		X
5.	40	46	X	X
6.	50	60	X	X
7.	60	62	X
8.	70	62	X
9.	80	44	X
10.	90	30
11.	100	26		X
12.	110	18		X
13.	120	42	X	X
14.	130	56	X	X
15.	140	60	X

Obliczenia i wnioski.

Wartość X₂=Z_f

-wyznaczamy węzły fali napięciowej

u(t), i(t) wartości chwilowe na linii

u(t)=(√X₂²+Z_f² /X₂)U₂ √2 sin(2π(l-x)/λ +θ) sin ωt

i(t)=(√X₂²+Z_f² /Z_f)I₂√2 cos(2π(l-x)/λ +θ) sin (ωt-θ)

θ=X₂/Z_f =-π/2 θ∈[-π/2, π/2]

Węzły fali napięciowej nie występują w punktach jak dla stanów jałowego i zwarcia, tylko są przesunięte względem tych punktów o kąt θ, który z obliczeń wynosi -π/2 i nie pokrywa się z pomiarami, gdzie wynosi w przybliżeniu -π/4.

8. Końcowe wnioski.

Linię długą potraktowaliśmy jako bezstratną, ponieważ przy zasilającej linię wysokiej częstotliwości wartości reaktancji wielokrotnie przewyższały wartości związane z rezystancją wzdłużną i admitancję poprzeczną linii (które to można było pominąć). Dlatego też przy obliczaniu impedancji falowej uwzględnia się tylko reaktancje. Ponieważ stratność linii związana jest z rezystancją i admitancją, które się pomija, a więc linie uważamy za bezstratną.

Na ogół wyniki pomiarów zgadzają się z wynikami obliczeń. Także charakterystyki powstałe z pomiarów są podobne z wykresami otrzymanymi z komputera. Wyniki pomiarów nie do końca są prawidłowe, występowały błędy związane z fizycznym pomiarem wartości względnej napięcia na linii długiej (wraz ze wzrostem siły nacisku styku końcówki miernika na linię wychylenie miernika wzrastało.

---