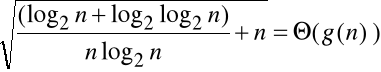AISDT - Kolokwium 1 19 listopada 2007
|
Podpis:
|
Zadanie 1 (4p)
Dane: liczba naturalna N Wynik: liczba naturalna S. Function S = Alg (N) If (N==1) S=1; Else S=N*Alg(N-1); End Dla podanego algorytmu podać równanie rekursywne na złożoność czasową, drzewo rekursji, wzór analityczny na złożoność czasową t(N) i wynik S, gdy operacją dominującą jest mnożenie. |
Równanie rekursywne:
Drzewo rekursji:
t(N) = S= |
Zadanie 2 (4p)
Dane: liczba naturalna N Wynik: liczba naturalna S. Function S = Alg (N) S=0; For I=1:N K=1; While (K<=N-I) K=K+1; End S=S+K; End Dla podanego algorytmu podać wzór analityczny na złożoność czasową t(N) i wynik S, gdy operacją dominującą jest dodawanie. |
t(N) =
S= |
Zadanie 3 (4p)
Znaleźć najprostszą postać funkcji g(n) dla której prawdziwe jest oszacowanie: Udowodnić jego prawdziwość za pomocą twierdzenia o granicy.
|
g(n) = Podać dowód: |
Zadanie 4 (4p)
Algorytm rec_power dla m=(1,0,1,a,1,b,1)NKB wykonał 11 mnożeń. Określić a, b i m. |
a= ....... , b= ........ m dziesiętnie =............... |
Zadanie 5 (4p)
Algorytm rekurencyjny Euklidesa z operacją mod euclid_rec(a,b) wykonano na danych pesymistycznych 5 bitowych. Określić a, b, liczbę wywołań euclid_rec (razem z wywołaniem z programu głównego) i wynik algorytmu. |
a= .......... b= .......... liczba wywołań = .......... wynik algorytmu = ......... |
Zadanie 6 (4p)
Mamy algorytm heapify(i), i jest indeksem kopca. Wypisać sekwencję wywołań heapify (bez wewnętrznych wywołań rekurencyjnych) przekształcającą tablicę [1,4,5,7,8] w kopiec typu max. Ile porównań oraz wzajemnych przestawień wymaga każde z tych wywołań. Dlaczego złożoność heapify nie jest tu stała? |
Heapify(......) L.porówn.=..... L.przest.=......... Heapify(......) L.porówn.=..... L.przest.=......... Heapify(......) L.porówn.=..... L.przest.=......... Heapify(......) L.porówn.=..... L.przest.=......... Dlaczego? ....................................................... ......................................................................... ......................................................................... ......................................................................... |
Zadanie 7 (4p)
Algorytmem quicksort sortujemy tablicę a= [4,3,1,2,6,5,7]. Pokazać tablicę a oraz indeks j po kolejnych wykonaniach partition, aż do posortowania. Zliczyć liczbę porównań w każdym wykonaniu partition. Podkreślać bieżące elementy dzielące. Obliczyć złożoność czasową t wykonania quicksort. |
a=[................................] (na początku) a=[................................], j=......., l.por.=......... a=[................................], j=......., l.por.=......... a=[................................], j=......., l.por.=......... a=[................................], j=......., l.por.=......... t=................................ |
Zadanie 8 (4p)
Zakładamy, że countsort wykonuje n+m operacji dominujących (ozn. jak na wykładzie). Radixsort sortuje ciąg 1000 danych 24-bitowych i dzieli je na grupy e-bitowe (takie że podział jest całkowity). Dobrać e, aby złożoność czasowa algorytmu była minimalna. |
e=...... Uzasadnić.
|
Wyszukiwarka
Podobne podstrony:
OGROCKI, AISDTkol1pop, AISDT - Kolokwium 1
OGROCKI, AISDEkolpopr, AISDT - Kolokwium 1
OGROCKI, AISDEkol1, AISDT - Kolokwium 1
do kolokwium interna
WODA PITNA kolokwium
KOLOKWIUM 2 zadanie wg Adamczewskiego na porownawczą 97
kolokwium 1
Materiały do kolokwium III
Fizjologia krążenia zagadnienia (II kolokwium)
Algebra liniowa i geometria kolokwia AGH 2012 13
analiza funkcjonalna kolokwium
kolokwiumzTMIC
kolokwium probne boleslawiec id Nieznany
więcej podobnych podstron