1.WIADOMOŚCI WSTĘPNE.

1.1 Cel ćwiczenia.

Celem ćwiczenia jest zapoznanie ze zjawiskiem rezonansu szeregowego w obwodzie RLC, wyznaczenie częstotliwości rezonansowej i współczynników dobroci obwodów oraz zmierzenie nieznanej indukcyjności metodą rezonansową.

1.2 Wstęp teoretyczny.

Rezonansem nazywamy zjawiska szubkiego wzrostu amplitudy drgań układu fizycznego, gdy częstotliwość zewnętrznych drgań wymuszających jest zbliżona do częstotliowści drgań własnych układu - amplituda osiąga wartość maksymalną gdy obie te częstotliwości są sobie równe.

Jednym z rodzajów rezonansu jest rezonans elektromagnetyczny występujący m.in. w szeregowym obwodzie RLC ( szeregowo połączone : opornik o oporze R , cewka o indukcyjności L i kondensator o pojemności C ) podłączonym do źródła prądu zmiennego : E ( t ) = E0 sin t .

Dla takiego układu natężenie prądu będzie się zmieniać w sposób sinusoidalny , z taką samą częstotliwością jaką wykazuje źródło prądu : I ( t ) = I0 sin ( t - ) , przy czym wartości amplitudy I0 oraz różnicy faz zależą od wielkości R , L , C , E0 oraz w następujący sposób :

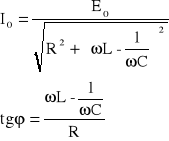
Wyrażenie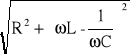
nazywamy zawadą układu RLC i stanowi ono swego rodzaju oporność tego układu. Widać wyraźnie , że przy ustalonych wartościach układu : R , L , C - amplituda I0 osiągnie wartość największą przy najmniejszej wartości zawady , a zatem gdy :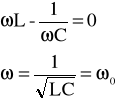
.

Wartość amplitudy jest wówczas równa : I0 = E0 / R.

Pulsacja , przy której pojawia się najwyższa wartość I0 nazywamy pulsacją rezonansową a odpowiadającą jej częstotliwość :
nazywamy częstotliwością rezonansową.

Należy zauważyć , że wartość amplitudy natężenia prądu dla częśtotliwości rezonansowej zależy tylko od oporu R , podczas gdy indukcyjność L i pojemność C mają wpływ na wartość częstotliwości rezonansowej.

Przy przechodzeniu elektronów przez opornik obserwuje się straty ich elektrycznej energii potencjalnej , która ulega przemianie w ciepło. To termodynamiczne nieodwracalne zjawisko nazywamy wydzielaniem ciepła Joule'a. Względne straty energii w obwodzie RLC są proporcjonalne do wielkości zwanej współczynnikem dobroci układu : Q = ( 2 E ) / E ( t ).

Jedną z metod wyznaczania współczynnika dobroci jest pomiar napięcia skutecznego Uc na kondensatorze podczas rezonansu przy znajomości wartości napięcia zasilającego Uwy : Q = Uc / Uwy.

1.3 Układ pomiarowy.

W skład układu pomiarowego wchodzą :

- generator akustyczny ,

- badany obwód RLC ,

- miliamperomierz prądu zmiennego ,

- woltomierz elektroniczny.

1.4 Przebieg pomiarów.

- w obwodzie RLC zmierzenie zależności natężenia prądu od częstotliwości dla stałej wartości napięcia zasilającego obwód ,

- zmierzenie napięcia na kondensatorze podczas rezonansu .

Pomiary wykonywane były dla trzech różnych rezystancji R1 , R2 , R3 , trzech różnych pojemności C1 , C2 , C3 i indukcyjności L.

2.TABELE POMIAROWE.

2.1 R1 + C1

Uwy = 2V

f [ Hz ]	I [ mA]	f [ Hz ]	I [ mA ]	f [ Hz ]	I [ mA ]
2000	2,1	3000	12,5	4000	6,3
2100	2,4	3100	17,0	4100	5,6
2200	2,7	3200	23,0	4200	5,1
2300	3,1	3300	23,3	4300	4,7
2400	3,6	3400	19,2	4400	4,4
2500	4,2	3500	14,2	4500	4,1
2600	5,0	3600	11,3	4600	3,9
2700	6,1	3700	9,2	4700	3,8
2800	7,6	3800	7,9	4800	3,5
2900	9,4	3900	7,0	4900	3,4

f0 = 3300 Hz , Uc = 17,2 V

2.2 R2 + C1

Uwy = 2V

f [ Hz ]	I [ mA ]	f [ Hz ]	I [ mA ]	f [ Hz ]	I [ mA ]
2000	2,1	3000	13,5	4000	6,3
2100	2,4	3100	21,6	4100	5,7
2200	2,8	3200	39,3	4200	5,2
2300	3,2	3300	40,6	4300	4,8
2400	3,6	3400	26,6	4400	4,4
2500	4,3	3500	15,5	4500	4,2
2600	5,1	3600	12,0	4600	3,9
2700	6,2	3700	9,7	4700	3,7
2800	7,8	3800	8,3	4800	3,5
2900	10,1	3900	7,1	4900	3,2

f0 = 3300 Hz , Uc = 30V

2.3 R3 + C1

Uwy = 2V

f [ Hz ]	I [ mA ]	f [ Hz ]	I [ mA ]	f [ Hz ]	I [ mA ]
2000	2,1	3000	14,7	4000	6,4
2100	2,4	3100	24,7	4100	5,8
2200	2,8	3200	54,0	4200	5,2
2300	3,1	3300	56,5	4300	4,8
2400	3,7	3400	24,8	4400	4,5
2500	4,3	3500	16,2	4500	4,1
2600	5,2	3600	12,7	4600	3,9
2700	6,2	3700	10,0	4700	3,7
2800	7,9	3800	8,5	4800	3,5
2900	10,3	3900	7,2	4900	3,4

f0 = 3300 Hz , Uc = 42V

2.4 R1 + C2

Uwy = 2V

f [ Hz ]	I [ mA ]	f [ Hz ]	I [ mA ]	f [ Hz ]	I [ mA ]
2000	0,44	5900	11,71	6700	7,70
3000	0,80	6000	14,81	6800	6,80
4000	1,42	6100	18,80	6900	5,50
5000	3,0	6200	20,20	7000	5,40
5500	5,33	6300	18,50	7500	3,37
5600	6,43	6400	13,50	8000	2,57
5700	7,80	6500	11,10	8500	2,10
5800	9,04	6600	9,10	9000	1,79

f0 = 6200 Hz , Uc = 29,4 V

2.5 R1 + C3

Uwy = 2V

f [ Hz ]	I [ mA ]	f [ Hz ]	I [ mA ]	f [ Hz ]	I [ mA ]	f [ Hz ]	I [ mA ]
2000	0,21	7000	2,48	8300	16,21	8800	8,62
3000	0,35	7500	3,99	8400	18,00	8900	7,13
4000	0,54	8000	8,07	8500	17,30	9000	6,42
5000	0,82	8100	9,95	8600	14,52	9500	3,72
6000	1,30	8200	13,03	8700	12,26	10000	2,88

f0 = 8400 Hz , Uc = 36 V

2.6 Zebranie wyników.

	R1 + C1	R2 + C1	R3 + C1	R1 + C2	R1 + C3
f0 [ Hz ]	3300	3300	3300	6200	8400
L [ mH ]	37	38	38	38	38
Q	8,6	15	21	14,7	18

( C1 = 62,53 nF , C2 = 17,33 nF , C3 = 9,27 nF ) 5%

R1 > R2 > R3

3. PRZYKŁADOWE OBLICZENIA.

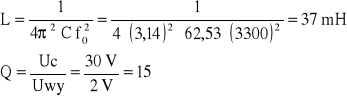
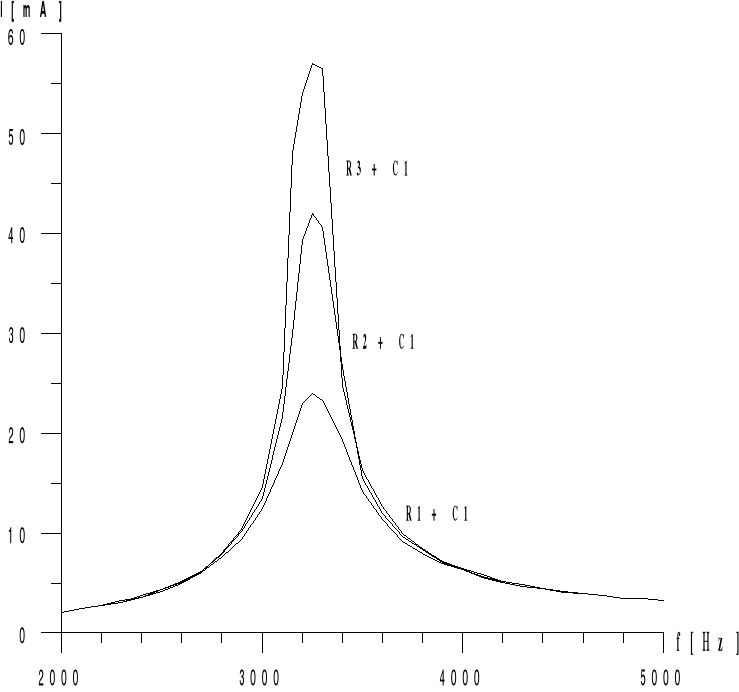
4.KRZYWE REZONANSOWE.

5.ANALIZA BŁĘDÓW.

Błąd względny L / L wyznaczamy metodą pochodnej logarytmicznej :

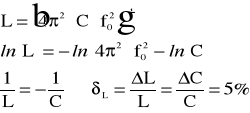
L = 38 mH 5 % = ( 38 1,9 ) mH

6.UWAGI I WNIOSKI.

Na podstawie krzywych rezonansowych możemy ustalić , że opór R1 > R2 - amplituda w czasie rezonansu ma wartość większąw przypadku R2 , a jest ona odwrotnie proporcjonalna do oporu.

W zgodzie z przewidywaniami pozostaje wzajemny stosounek uzyskanych częstotliwości rezonansowych dla różnych pojemności kondensatora - częstotliwość ta jest odwrotnie proporcjonalna do pierwiastka z pojemności , czyli dla większej pojemności obserwuje się rezonans przy mniejszej częstotliwości.

Ponadto , jak należało się spodziewać , współczynniki dobroci mają wartość mniejszą , a zatem obserwuje się większe straty energii dla większych wartości oporów.

Pomimo teoretycznych przewidywań o równej wartości amplitudy I0 dla równych wartości oporów , otrzymano różne wysokości krzywych rezonansowych dla odpowiednich oporów. Wydaje się to być związane z różnicami we współczynnikach dobroci - im większy współczynnik dobroci , tym większa krzywa rezonansowa.

6.UWAGI I WNIOSKI.

Na podstawie uzyskanych krzywych rezonansowych możemy ustalić , że faktycznie R1 > R2 >R3 , oraz , że prąd płynący przez obwód podczas rezonansu jest odwrotnie proporcjonalny do rezystancji. Zauważyć można również , iż częstotliwość rezonansowa zależy od pojemności kondensatora i indukcyjności cewki , i nie zależy od rezystancji , przy czym im większa pojemność tym częstotliwośc rezonansowa jest niższa. Możemy też zauważyć , że dobroć układu drgającego RLC jest odwrotnie proporcjonalna do rezystancji R, a więc im rezystancja mniejsza tym większa jest krzywa rezonansowa.

---