1. Przedstaw metody wyznaczania stałych K i C.

Wyznaczanie stałych filtracji przy Δp=const.

Różniczkujemy:

Wykonanie pomiaru:

Gdy n≥3 stosujemy metodę najmniejszych kwadratów.

Dla n=2 korzystamy z równania:

2. Opisz filtrację z tworzeniem osadu przy stałej prędkości przepływu.

Dla osadu nieściśliwego

Dla osadu ściśliwego

3. Scharakteryzuj filtrację dwustopniową

Jest powiązana z filtracją przy stałej prędkości filtracji z filtracją przy stałym ciśnieniu. Przyczyną jej stosowania jest dążność do stworzenia dogodnych warunków we wstępnym okresie filtracji, gdy tworzą się pierwsze warstewki osadu. W takim przypadku nie powinno się stosować dużych różnic ciśnień gdyż mogłaby powodować złą jakość filtracji (część cząstek przechodziłaby do filtratu). W miarę wzrostu długości warstwy osadu opór przy przepłynięciu cieczy wzrasta i otrzymanie stałej prędkości wymaga zwiększenia Δp. Gdy wartość Δp osiągnie maksimum rozpoczyna się drugi stopień filtracji: pod stałym ciśnieniem.

4. Omów przewodnictwo cieplne gazów, cieczy i ciał stałych.

Przewodnictwo ciepła w gazach polega na wymianie energii kinetycznej cząsteczek poruszaj się bezładnie i zderzających się ze sobą. Cząsteczki te w obszarze o wyższej temp mają wyższą energię. Współczynnik przewodzenia ciepła dla gazów waha się najczęściej w granicach:

λ rośnie zawsze wraz z temperaturą.

Współczynnik przewodzenia ciepła dla cieczy waha się najczęściej w granicach: λ=0,1 - 0,7.

λ dla większości cieczy maleje ze wzrost temp.

Współczynnik przewodzenia ciepła dla ciał stałych (jednorodnych) waha się najczęściej w granicach: λ=0,04 - 460. λ dla ciał stałych wykazuje niemal prostoliniową zależność od temperatury. W materiałach izolacyjnych (λ do 0,1), materiałach budowlanych (λ=0,5:3), w metalach (λ=2:460)

5. Opisz przewodzenie ciepła przez ściankę płaską wielowarstwową

Często mamy do czynienia z przewodzeniem ciepła przez ściankę płaską wielowarstwową, przy czym każda warstwa może mieć inną grubość i znacznie różniące się wartości współczynnika przewodzenia ciepła. Całkowity spadek temp w całej ściance płaskiej jest równy sumie spadków temp w poszczególnych warstwach. Opór termiczny stawiany przez ściankę płaska wielowarstwową jest równy sumie oporów termicznych poszczególnych warstw ścianki płaskiej.

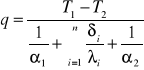
(rysunek)

6. Omów konwekcję naturalną w przestrzeni ograniczonej.

Konwekcja swobodna zachodzi na ogół miedzy dwoma płaszczyznami niezbyt oddalonymi: w wąskich szczelinach, kanałach poziomych lub pionowych, przestrzeniach pierścieniowych. Brak jest w takich przypadkach dobrze wykształcony prądów konwekcyjnych wznoszących i opadających, konwekcja jest mocno związana z przewodzeniem ciepła. Tego rodzaju konwekcję traktujemy jako specyficznie pojmowany proces przewodzenia ciepła wprowadzając jednocześnie pojęcie zastępczego współczynnika przewodzenia ciepła λz oraz wielkość charakteryzującą wpływ konwekcji:

i λz = λ

7. Scharakteryzuj siły działające na utworzony pęcherzyk pary podczas wrzenia.

W momencie tworzenia się pęcherzyka działają na niego 2 siły: siła ciężkości otaczającej go cieczy i siła napięcia powierzchniowego samej powierzchni pęcherzyka. Prężność pary w powstałym pęcherzyku musi być tak duża, by siła jej parcia zrównoważyła siły napięcia powierzchniowego i parcia cieczy (pęcherzyk kulisty).

siła która stara się rozerwać pęcherzyk

siła powstałą pod wpływem napięcia powierzchniowego, która przeciwstawia się jego rozerwaniu

-pęcherzyk istnieje i rozwija się

następuje kondensacja pęcherz

8. Scharakteryzuj przenikanie ciepła

Przenikanie to przenoszenie ciepła przez przegrodę. Zjawisko przenikania obejmuje przejmowanie ciepła z jednego ośrodka, przewodzenie przez przegrodę i przejmowanie ciepła przez drugi ośrodek. Ciepło przenika przez ścianę z ośrodka o temp wyższej

tz1 do ośrodka o temperaturze niższej tz2.

9. Przedstaw bilans materiałowy kolumny rektyfikacyjnej.

Do kolumny rektyfikacyjnej wpływa F kmoli/s o stężeniu x_F ułamka molowego składnika bardziej lotnego, wypływa natomiast D kmoli/s rektyfikatu o zawartości x_D ułamka molowego składnika bardziej lotnego oraz W kmoli/s cieczy wyczerpanej o stężeniu xw ułam molowego składnika bardziej lotnego. Bilans materiałowy całej kolumny rektyfikacyjnej można ująć: F=D+W, a dla składnika bardziej lotnego: Fx_F=Dx_D+Wx_W

Po przekształceniu otrzymujemy: D(x_D-x_F)=W(x_F-x_W), W/D= x_D-x_F/ x_F-x_W

Z tego równania wynika, że jeżeli skład surówki xF rektyfikatu xD oraz cieczy wyczerpanej xw zostały ustalone, wtedy z określonej liczby moli surówki F uzyskamy ściśle określona liczbę moli rektyfikatu D i cieczy wyczerpanej W.

10. Przedstaw bilans materiałowy półki zasilającej.

Jeżeli F oznacza liczbę kmoli surówki doprowadzanej w jednostce czasu do kolumny rektyfikacyjnej, wtedy uwzględniając strumienie cieczy i pary dopływające do półki zasilającej i odpływające z niej możemy ułożyć bilans materiałowy półki zasilającej:

L+G'+F=L'+G

Należy znaleźć związek między liczbą moli cieczy płynącej w górnej części kolumny L a liczbą moli cieczy płynącej w dolnej części kolumny rektyfikacyjnej. Podobnie należy ustalić związek między molowym natężeniem przepływu pary w górnej (G) i dolnej (G') części kolumny. Rozwiązanie tego zagadnienia staje się możliwe po uwzględnieniu wpływu stanu cieplnego surówki na strumienie cieczy i pary w obu częściach kolumny rektyfikacyjnej.

---