Nr ćw. 103	Data			Wydział Elektryczny		Semestr III		Grupa I-1
Prowadząca:				Przygotowanie		Wykonanie		Ocena

Temat: Wyznaczanie modułu Younga metodą wydłużenia

1. Własności sprężyste ciał

Gdy odkształcenie (makroskopowa deformacja ciała) zanika po odjęciu siły zewnętrznej, to nazywamy je sprężystym, natomiast odkształcenie nie znikające po odjęciu siły nazywamy plastycznym.

2. Siły oddziaływania międzyatomowego. Zależność energii potencjalnej i siły oddziaływania w funkcji odległości w układzie 2 atomów.

Między atomami działają siły zależne od wzajemnej odległości. Zależność siły oraz energii potencjalnej w układzie 2 atomów przedstawiaja wykresy:

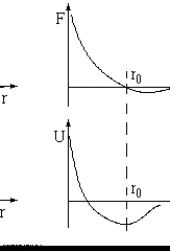
Przy pewnej odległości r0, siła działająca między atomami ma wartość równą zero, a energia potencjalna układu osiąga minimum. Jest to położenie równowagi. Gdy ten stabilny stan zostanie zakłocony przez np. siłę zewnętrzną, będzie on "próbował" powrócić do stanu równowagi (o minimalnej energii) --pojawia się siła sprężystości.

3. Zależność odkształcenia od naprężenia. Prawo Hooke'a

Naprężeniem normalnym nazywamy stosunek siły normalnej (prostopadłej) do wielkości powierzchni, na którą działa:

Pod wpływem naprężeń normalnych ciało ulega odkształceniu: wydłużeniu lub skróceniu. Stosunek przyrostu długości do długości początkowej nazywamy odkształceniem względnym :

Wydłużenie względne jest wprost proporcjonalne do naprężenia normalnego:

Jest to prawo Hooke'a, słuszne bez względu na zwrot odkształcenia. Współczynnik E nazywamy modułem Younga. Jest to wartość naprężenia potrzebna do wydłużenia ciała o długość początkową.

Jednakże, tej wiadomości nie da się bezpośrednio wykorzystać w praktyce do pomiaru wielokści modułu Younga, ponieważ granica stosowalności prawa Hooke'a (odkształcenie, dla którego ciało zachowuje własności sprężyste) dla większości ciał leży poniżej moduły Younga. Ale, rozszerając w/w wzór otrzymujemy:

Zatem, jeśli w prostokątnym układzie współrzędnych na osi X odłożymy wydłużenie względne, a na osi Y stosunek siły do powierzchni przekroju, to tangens kąta nachylenia powstałej prostej będzie modułem Younga.

4. Zasada pomiaru

Do długiego drutu umocowanego końcem w suficie przymocowujemy obciążenie początkowe celem wyprostowania zgięć. Przymocowaną osiowo poziomicę ustalamy w położeniu zerowym kręcąc pokrętłem śruby mikrometrycznej i odczytujemy z jej podziałki wartość początkową. Podobnie postępujemy przy dokładaniu kolejnych ciężarków. Po osiągnięciu obciążenia maksymalnego zdejmujemy ciężarki w odwrotnej kolejności. Jeśli odpowiednie wartości są zgodne, to znaczy że zakres obciążeń nie przekroczył granicy sprężystości.

Przekrój drutu obliczamy z pomiarów średnicy za pomocą śruby mikrometrycznej.

5. Pomiary i obliczenia

pomiary długości i średnicy drutu

dł. drutu l =1,2540,001 m

Numer pomiaru	1	2	3	4	5	6	7	8	9	10
średnica drutu [mm]	0,5	0,5	0,49	0,49	0,5	0,49	0,51	0,5	0,5	0,5

=0,01 mm

Uśredniając powyższe pomiary i korzystając z odchylenia standardowego otrzymujemy:
śr. drutu =0,4980,019 [mm]
Zatem, promień drutu r=0,2490,009 [mm]
Pole przekroju S=r2=0,1950,014 [mm2]

pomiary wydłużeń

obciążenie [g]:	m0+101,32	m0+205,41	m0+300,70	m0+398,30	m0+503,08	m0+602,46	m0+697,38
Zn rosnąco [mm]	0,26	0,31	0,35	0,38	0,42	0,46	0,50
Zn malejąco [mm]	0,26	0,30	0,35	0,38	0,41	0,45	0,50

Zn=0,01 [mm]
masa początkowa m0=396,950,01 [g]
położenie zerowe (wydłużnie pod wpływem obciążenia początkowego) Z0=0,200,01 [g]
Jak widać granica sprężystości nie została przekroczona.
Uśredniając odpowiednie wartości, oraz stosując odchylenie standardowe (×3) w celu obliczenia błedu tam gdzie wyniki się różnią, a błąd systematyczny tam gdzie są takie same w powyższej tabelce, otrzymujemy:

[mm]	0,26	0,305	0,35	0,38	0,415	0,455	0,5
	0,010	0,021	0,010	0,010	0,021	0,021	0,010

obliczanie naprężeń

Następnie korzystając z wzoru w pkt.3 obliczamy naprężenie normalne . Błąd obliczamy korzystając z różniczki zupełnej:

, i otrzymujemy:

[N/m2]	25066814	30303342	35097162	40007192	45278432	50278011	55053217
[N/m2]	1800172	2176128	2520299	2872814	3251262	3610206	3953042

obliczanie odkształceń względnych

Korzystając z wzoru na odkształcenie względne z pkt. 3 obliczamy . Błąd obliczamy korzystając z rózniczki zupełnej:

, otrzymujemy:

	0,0000478	0,0000837	0,0001196	0,0001435	0,0001714	0,0002033	0,0002392
	0,0000080	0,0000170	0,0000081	0,0000081	0,0000171	0,0000171	0,0000082

Odkładając odpowiednio na osiach otrzymujemy wykres:

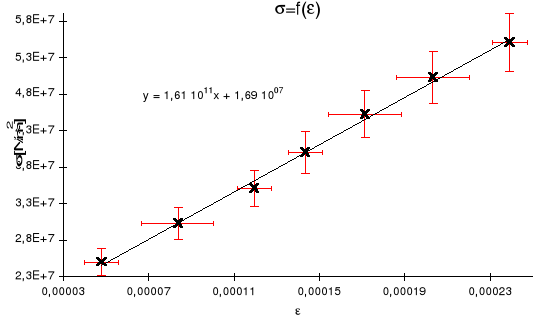
czyli E ma wartość 1,611011 [N/m2]Pozostaje jeszcze do obliczenia błąd E. Jest on średnią błędów En. Za pomocą różniczki zupełnej otrzymujemy następujący wzór:

który pozwala uzyskać:

En

1,251011

9,941010

4,091010

3,571010

4,521010

3,851010

2,44E+10

obliczając średnią mamy: E=5,851010 [N/m2].

Ostateczny wynik to E=(1,610,59)1011 [N/m2].

6. Wnioski i uwagi

Badany materiał to najprawdopodobniej stal, choć w otrzymanym zakresie (1,012,20)1011 [N/m2] mieści się również wiele innych materiałów np. miedź, mosiądz, konstantan, nikiel, żelazo, platyna. Świadczy to o tym, że wyniki są niezbyt wiarygodne, być może ze względu na niezadowalająco sztywne przymocowanie podpórki ze śrubą mikrometryczną do ściany, oraz pewną niejednoznaczność przy ustawianiu poziomicy, jej punkt podparcia był dość trudny do uchwycenia.

---