1. Podać I i II twierdzenie Tissota i uzasadnić warunek dla odwzorowań wiernokątnych. Od czego zależy skala długości w odwzorowaniach wiernopolowych a od czego w wiernokątnych?

I twierdzenie Tissota:

W dowolnym regularnym odwzorowaniu jednej powierzchni na drugą istnieje (co najmniej jedna) siatka ortogonalna, która odwzorowuje się na siatkę ortogonalną. Siatka ta nazywa się siatką główną.

II twierdzenie Tissota:

Obrazem graficznym zniekształceń długości we wszystkich kierunkach wychodzących z jednego punktu powierzchni jest elipsa, której półosie są równe zniekształceniom w kierunkach głównych.

Uzasadnienie warunku dla odwzorowań wiernokątnych:

A = A gdy F = 0 i jednocześnie (E/H)*(r/M) = 1

ctgA = (m_B/m_LsinO)ctgA + ctgO gdy O = 90⁰ i m_B = m_L

Skala długości w odwzorowaniach wiernopolowych zależy od położenia i azymutu a w wiernokątnych tylko od położenia.

2. Podać postać I formy kwadratowej i omówić jej wykorzystanie w badaniu powierzchni uczestniczących w odwzorowaniu.

gdzie: u = const, v = const - linie parametryczne

dla F = 0 - siatka linii parametrycznych jest ortogonalna

3. Co to są zniekształcenia odwzorowawcze i podać ich postać dla pól i długości.

Zniekształcenia odwzorowawcze to zniekształcenia (nie błędy) powstałe przy odwzorowaniu bryły ziemskiej na płaszczyznę.

Zniekształcenie pola:

p = dP'/dP

Zniekształcenie długości:

m = ds'/ds.

4. Omówić ogólną teorię odwzorowań azymutalnych normalnych kuli.

Obrazami równoleżników są współśrodkowe okręgi, których środek znajduje się w środku bieguna, obrazami południków są proste zbiegające się w biegunach.

X = R sinp cos

Y = R sinp sin

Z = R cosp

W zależności od położenia środka rzutu wyróżniamy:

- rzut centralny

- rzut stereograficzny

- rzut ortograficzny

Koło wielkie przechodzące przez dany punkt G nazywamy wertykałem, a koło małe, którego wszystkie punkty są równo oddalone od punktu G nazywamy almukantaratem.

Zastosowanie:

- do sporządzania map radiokomunikacji morskiej i lądowej oraz map telekomunikacyjnych i pocztowych

- ilustrowanie zjawisk sejsmicznych

- opracowywanie map ciał niebieskich

5. Wyprowadzić zależność dla odwzorowania walcowego normalnego równopolowego, normalnego równoodległościowego, normalnego wiernokątnego kuli.

Odwzorowanie równopolowe:

ab = 1

czyli

, dla

Zatem wzory tego odwzorowania będą miały postać:

x = R sin

y = R 

Odwzorowanie równoodległościowe powstaje przez rozwinięcie na płaszczyźnie wszystkich południków i równika wiernie, czyli skala w kierunku południków powinna być równa jedności:

dla

Zatem wzory tego odwzorowania będą miały postać:

x = R 

y = R 

Odwzorowanie wiernokątne:

Warunek równokątności:

co prowadzi do równania

Zatem

dla

Wzory tego odwzorowania będą miały postać:

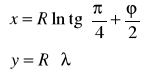
6. Odwzorowanie Gaussa - Krugera i zdefiniować w nim:

- zbieżność południków

- skale długości i pól

- współrzędne cechowane

Odwzorowanie Gaussa-Krügera jest to wiernokątne, poprzeczne, walcowe odwzorowanie elipsoidy obrotowej na płaszczyznę, realizowane w wąskich pasach południkowych.

Spełnia następujące warunki:

- południk środkowy (osiowy) pasa odwzorowuje się na odcinek linii prostej

- skala długości na południku środkowym jest równa jedności: m₀=1, a₀=b₀=1

Kształt siatki kartograficznej:

- południk środkowy odwzorowuje się wiernie na odcinek linii prostej

- pozostałe południki na krzywe symetryczne względem południka środkowego (wklęsłością do obrazu południka środkowego)

- równik odwzorowuje się na odcinek linii prostej, prostopadłej do południka środkowego, równoleżniki - na linie krzywe symetryczne względem obrazu równika (wypukłością do obrazu równika)

Zbieżnością południków w odwzorowaniu nazywamy kąt zawarty między styczną do obrazu południka w danym punkcie a linią prostą przechodzącą przez ten punkt równolegle do osi x.

Elementarna skala długości:

Elementarna skala pól:

Współrzędne cechowane to współrzędne przesunięte tak, że wszystkie są dodatnie.

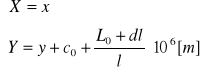
gdzie:

c₀ = 500 000 m

L₀ = długość geodezyjna południka środkowego w [°],

l - szerokość pasa odwzorowawczego w [°] (najczęściej 3° lub 6°)

dl = 3° dla pasa 6-stopniowego i dl =0° dla pasa 3-stopniowego

Najczęściej używa się elipsoid GRS-80 i Krasowskiego.

7. Scharakteryzować Układ Współrzędnych 2000 i podać różnice względem odwzorowania Gaussa - Krugera.

Układ współrzędnych „2000” (nowa wersja odwzorowania G-K):

- elipsoida WGS-84

- cztery 3-stopniowe pasy odwzorowawcze (15°, 18°, 21°, 24°),

- skala m₀ = 0.999923, X = x, Y = y + (5 500 000, 6 500 000, 7 500 000, 8 500 000) metrów dla kolejnych pasów odwzorowawczych

Odwzorowanie to jest obowiązującym odwzorowaniem dla mapy zasadniczej.

Układ współrzędnych „1992” (bonus):

- elipsoida WGS-84

- odwzorowanie Gaussa-Krugera

- jeden 12-stopniowy pas odwzorowawczy dla całej Polski (L₀ = 19°),

- skala m₀ = 0.9993, X = x - 5 300 000 m, Y = y + 500 000 m.

Odwzorowanie to jest obowiązującym odwzorowaniem dla map w skalach 1:10000 i mniejszych.

Różnice z G-K patrz pytanie wcześniej i sam oceń.

8. Podać jakie warunki powinny mieć funkcje f i g w odwzorowaniu aby było ono regularne.

Odwzorowanie nazywamy regularnym, gdy funkcje f i g spełniają następujące warunki:

a) każdej parze wartości parametrów u, v przyporządkowują jedną i tylko jedną parę wartości parametrów U, V

b) są ciągłe i co najmniej dwukrotnie różniczkowalne

c) są wzajemnie niezależne

---